дифуравнения / дифуравнения-1 / тема9

Тема: Системи лінійних диференціальних рівнянь

Теоретичні відомості

Означення. Нормальною системою диференціальних рівнянь називається система виду

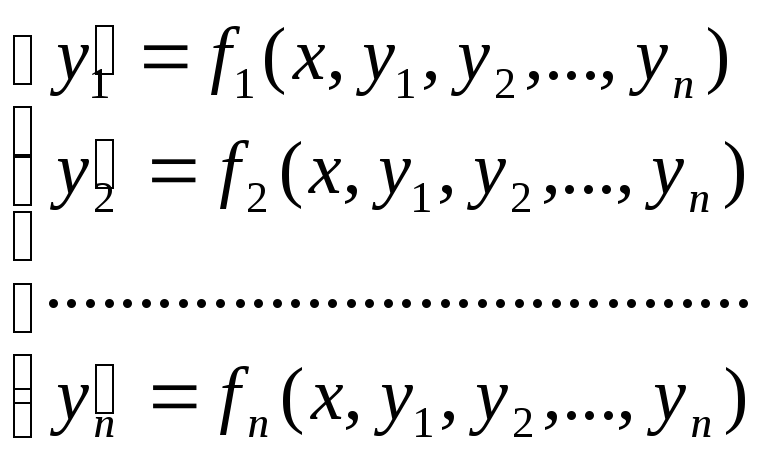(1)

Означення. Рішенням системи (1) називається сукупність функцій , які задовольняють всім рівнянням системи.

Означення. Загальним рішенням системи (1) називається сукупність рішень, які залежать від довільних констант

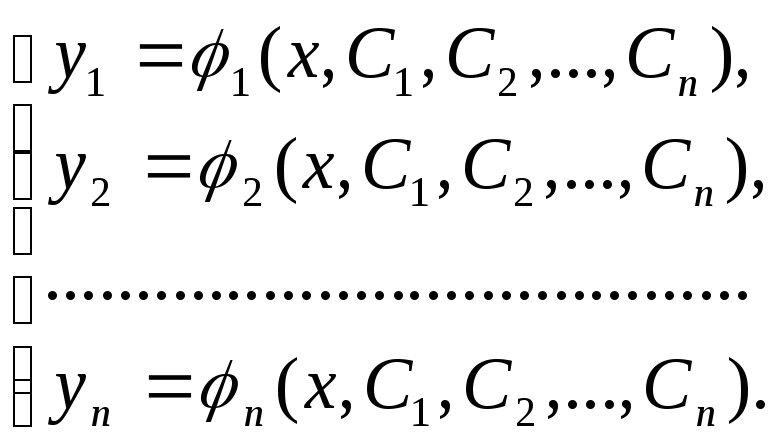
Означення. Частинним рішенням системи (1) називається рішення, яке задовольняє початковим умовам , де .

Розглянемо систему двох лінійних диференціальних рівнянь з двома невідомими функціями

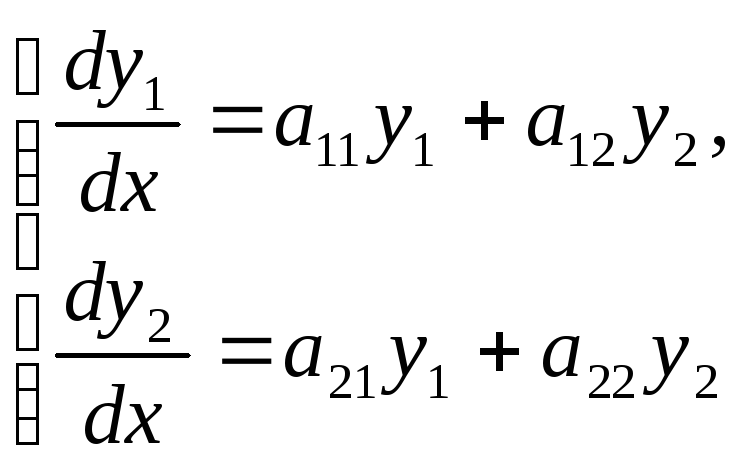, (2)

де . Застосуємо для розв’язання системи (2) метод виключення, який зводить розв’язання системи до розв’язання лінійного однорідного рівняння ІІ порядку з постійними коефіцієнтами.

Диференціюємо перше рівняння по :

. (3)

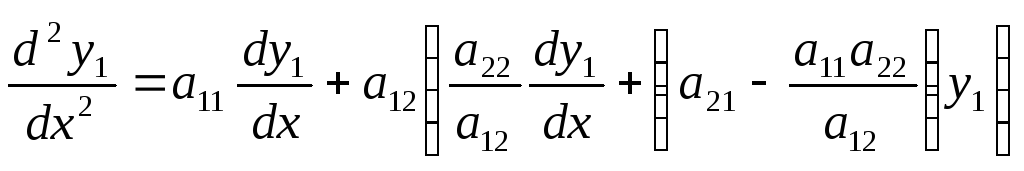З першого рівняння дістаємо: , тоді з другого рівняння отримаємо: . Підставимо вираз для в (3): , або . Отже, ми прийшли до лінійного однорідного рівняння або

. (4)

З рівняння (4) знайдемо функцію , після чого знайдемо .

Рівняння (4) може бути записане у вигляді

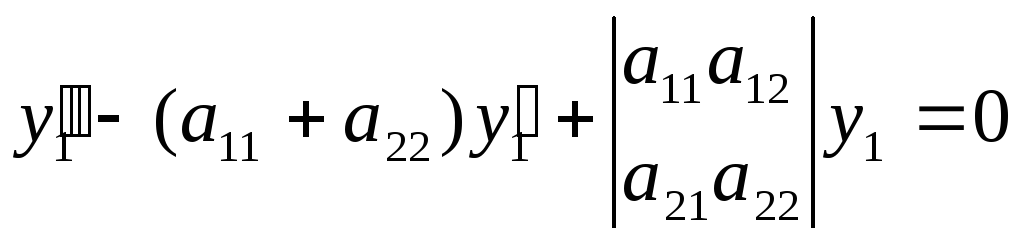
Практичні завдання

Завдання 1. Розв’яжіть систему лінійних диференціальних рівнянь:

1.1.

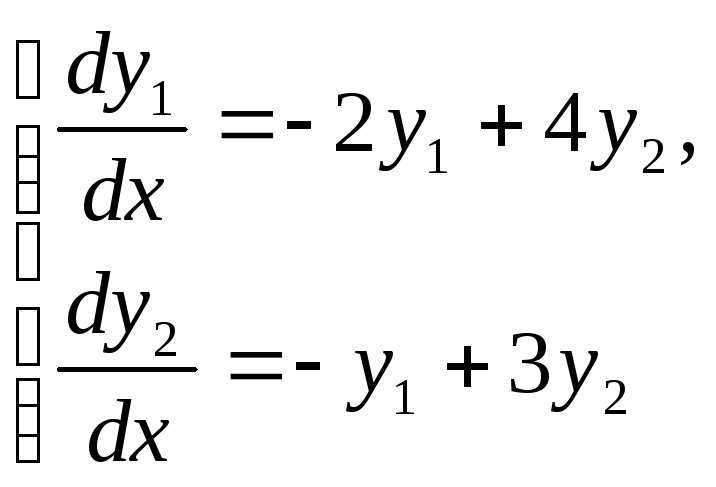
1.2.

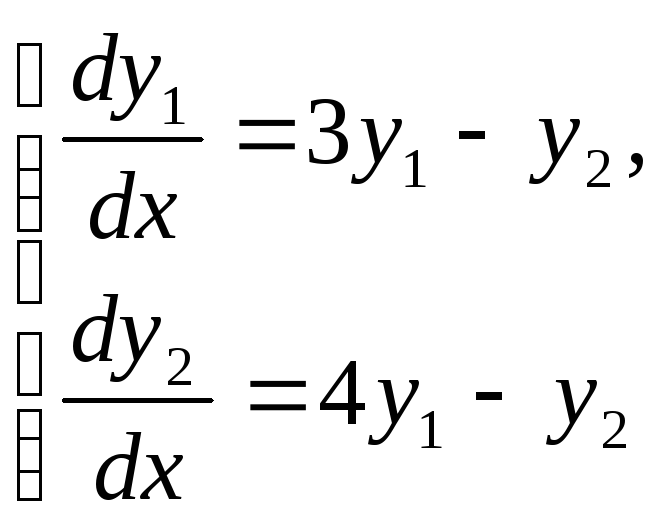
1.3.

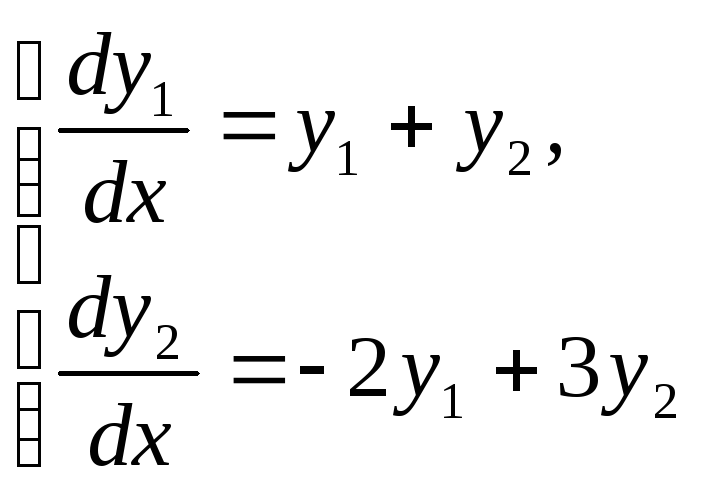
1.4.

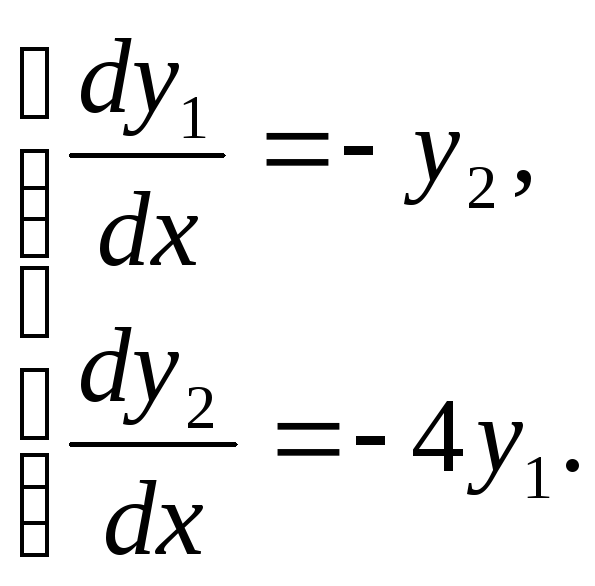
1.5.

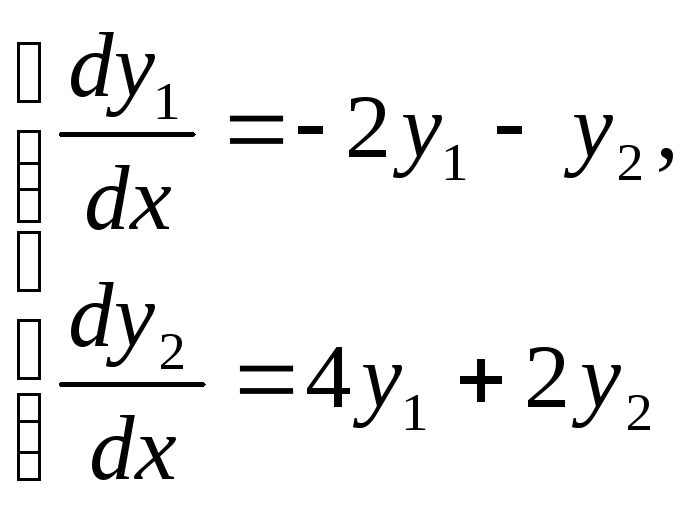
Завдання 2. Розв’яжіть задачу Коші:

2.1. 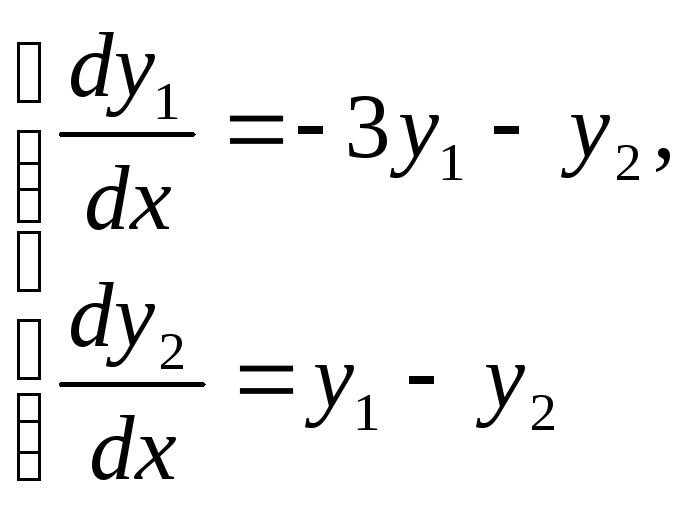, якщо

2.2. 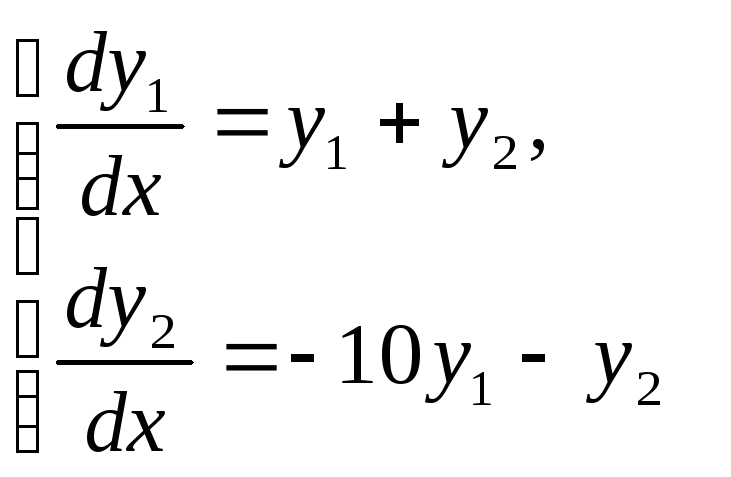, якщо

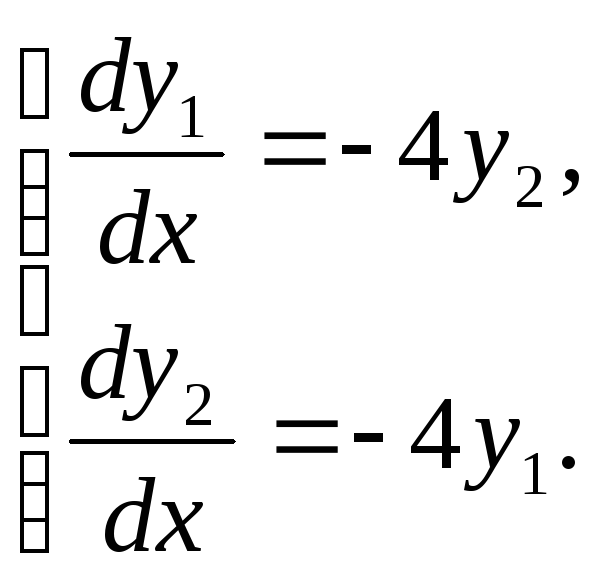2.3. , якщо