дифуравнения / дифуравнения-1 / тема4

Тема: Рівняння в повних диференціалах.

Теоретичні відомості.

Означення. Якщо в диференціальному рівнянні

(1.15)

ліва частина є повним диференціалом деякої функції від незалежних змінних і , то таке рівняння називається диференціальним рівнянням в повних диференціалах.

Інакше кажучи, рівняння (1.15) є рівнянням в повних диференціалах, якщо існує така функція , що

.

В цьому випадку диференціальне рівняння (1.15) можна подати у вигляді

(1.16)

і його загальний інтеграл

. (1.17)

Нехай функції і визначені і неперервні в деякій області і мають в цій області неперервні частинні похідні по і по . Необхідною і достатньою умовою того, щоб рівняння (1.15) було рівнянням в повних диференціалах, є виконання рівності

. (1.18)

Якщо умова (1.18) виконана, то загальний інтеграл можна записати у вигляді

, (1.19)

або

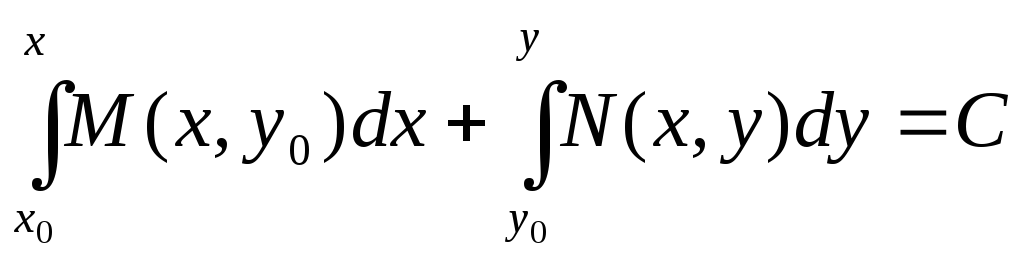, (1.20)

де точка належить області . Тут інтегрування проводилося по одній із змінних, інша змінна є при цьому параметром.

Рішення задачі Коші з початковими умовами в області , за умови, що в точці функції і водночас не перетворюються на нуль, отримаємо із загального інтегралу (1.19) або (1.20) при :

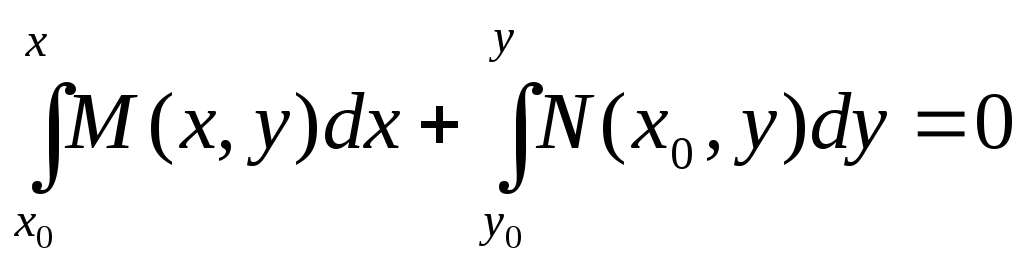, (1.21)

або

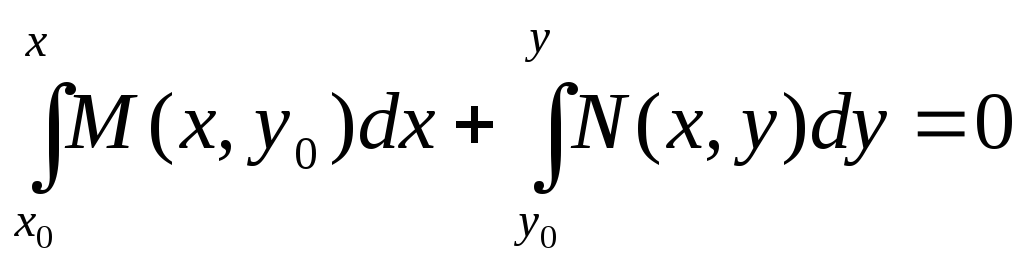. (1.22)

Практичні завдання.

Завдання 1. Знайти частинні похідні функцій:

1.1. .

1.2. .

1.3. .

1.4. .

1.5. .

1.6. .

Завдання 2. Знайти загальний інтеграл рівняння:

2.7. .

2.8. .

2.9. .

2.10. .

2.11. .

2.12. .

Завдання 3. Знайти частинний інтеграл рівняння, який задовольняє заданим початковим умовам:

2.13. , якщо .

2.14. , якщо .

2.15. , якщо .

Домашнє завдання: теоретичні відомості

Знайти загальний інтеграл рівняння .

Знайти частинний інтеграл рівняння , якщо .