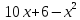Остальные (alldone)
ЦТ 2005 B3.Знаменатель несократимой дроби на 3
больше, чем числитель. Если дробь умножить
на ,
а затем у новой дроби числитель уменьшить
на 2 и знаменатель уменьшить на 19, то
получим дробь, обратную исходной. Найдите
произведение числителя и знаменателя
исходной дроби.
,
а затем у новой дроби числитель уменьшить
на 2 и знаменатель уменьшить на 19, то
получим дробь, обратную исходной. Найдите
произведение числителя и знаменателя
исходной дроби.
Решение
Пусть
 — исходная дробь, тогда
— исходная дробь, тогда — дробь, умноженная на
— дробь, умноженная на ,
, — дробь с уменьшенным числителем и
уменьшенным знаменателем. Получаем
уравнение
— дробь с уменьшенным числителем и
уменьшенным знаменателем. Получаем
уравнение

корни
которого и
и .
Первый корень посторонний, так как при
данном значении
.
Первый корень посторонний, так как при
данном значении ,
дробь сократима. При втором корне,
получаем несократимую дробь
,
дробь сократима. При втором корне,
получаем несократимую дробь .
.
Ответ: 40.
РТ 2 2006 В3.Число 58 разделили на некоторое натуральное число и получили, что неполное частное на 6 меньше остатка, а делитель на 2 больше остатка. Найдите остаток.
Решение
Пусть
 — делитель,
— делитель, — неполное частное,
— неполное частное, — остаток, тогда
— остаток, тогда ,
, ,
, ,
тогда
,
тогда или
или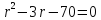 .
. ,
, .
Второй корень посторонний, поскольку
остаток всегда неотрицателен.
.
Второй корень посторонний, поскольку
остаток всегда неотрицателен.
Ответ: 10.
РТ 3 2009
В11.Знаменатель несократимой
дроби на 1 меньше, чем удвоенный числитель.
Если к дроби прибавить ,
а затем у новой дроби числитель увеличить
на 2, то получим дробь, обратную исходной.
Найдите произведение числителя и
знаменателя исходной дроби.
,
а затем у новой дроби числитель увеличить
на 2, то получим дробь, обратную исходной.
Найдите произведение числителя и
знаменателя исходной дроби.
Решение
|
Фраза |
Модель |
|
Числитель первоначальной дроби |
|
|
Знаменатель дроби на 1 меньше, чем удвоенный числитель. |
|
|
Дробь |
|
|
Если к дроби прибавить
|
|
|
а затем у новой дроби числитель увеличить на 2, |
|
|
то получим дробь, обратную исходной. |
|
|
Найдите произведение числителя и знаменателя исходной дроби. |
|
Убеждаемся,
что при
 дробь несократима.
дробь несократима.
Ответ: 45.
ЦТ 2009 В9.Задумано целое положительное число. К его записи приписали справа цифру 6 и из полученного числа вычли квадрат задуманного. Разность уменьшили на 80% и еще вычли задуманное число. В окончательном результате получили 0. Какое число задумано?
Решение
|
Фраза |
Модель |
|
Задумано целое положительное число. |
|
|
К его записи приписали справа цифру 6 |
|
|
и из полученного числа вычли квадрат задуманного. |
|
|
Разность уменьшили на 80% (осталось 20%) |
|
|
и еще вычли задуманное число. |
|
|
В окончательном результате получили 0. |
|
|
Какое число задумано? |
|
Ответ: 6.
ЦТ 2010 В8.Банка, имеющая форму правильной
четырехугольной призмы, частично
заполненная водой. Сторона основания
банки равна .
В эту банку опустили кубик, ребро которого
равно
.
В эту банку опустили кубик, ребро которого
равно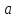 ,
при этом кубик лег на дно банки, а
поверхность воды поднялась на столько,
что стала касательной к верхней грани
кубика. Если вместо этого кубика опустить
кубик, ребро которого равно
,
при этом кубик лег на дно банки, а
поверхность воды поднялась на столько,
что стала касательной к верхней грани
кубика. Если вместо этого кубика опустить
кубик, ребро которого равно ,
то произойдет, то же самое. Найдите
,
то произойдет, то же самое. Найдите .
.
Решение
Пусть
 — объем воды находившейся в сосуде.
Когда в сосуд опустили кубик с ребром
— объем воды находившейся в сосуде.
Когда в сосуд опустили кубик с ребром ,
объем содержимого, с одной стороны, стал
равен
,
объем содержимого, с одной стороны, стал
равен ,
с другой стороны, объем равен
,
с другой стороны, объем равен .
Т.е. получили уравнение
.
Т.е. получили уравнение .
Когда опустили кубик во второй раз,
получаем еще одно уравнение
.
Когда опустили кубик во второй раз,
получаем еще одно уравнение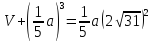 .
Вычитая из первого уравнения второе,
получаем
.
Вычитая из первого уравнения второе,
получаем

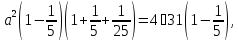

Ответ: 10.
Сканави
13.445 (5 изд) На столе стоит цилиндрическая
банка с водой. Радиус основания банки
равен .
Если в банку опустить шарик радиуса
.
Если в банку опустить шарик радиуса ,
то он ляжет на дно банки, а поверхность
воды при этом поднимется настолько, что
окажется касательной к шарику. Доказать,
что произойдет то же самое, если в эту
банку с тем же количеством воды опустить
шарик другого радиуса. Найти радиус
нового шарика и установить условия, при
которых он будет больше или меньше
радиуса данного шарика.
,
то он ляжет на дно банки, а поверхность
воды при этом поднимется настолько, что
окажется касательной к шарику. Доказать,
что произойдет то же самое, если в эту
банку с тем же количеством воды опустить
шарик другого радиуса. Найти радиус
нового шарика и установить условия, при
которых он будет больше или меньше
радиуса данного шарика.
Решается аналогично приведенному выше.
Ответ:
 ;
;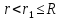 при
при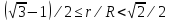 ,
, при
при .
.
РТ2 2012
В12.От пристани вниз по реке, скорость течения которой
вниз по реке, скорость течения которой км/ч, отходит плот. Через час вслед за
ним выходит моторная лодка, скорость
которой в стоячей воде 12 км/ч. Догнав
плот, лодка возвращается обратно. Найдите
сумму всех возможных значений
км/ч, отходит плот. Через час вслед за
ним выходит моторная лодка, скорость
которой в стоячей воде 12 км/ч. Догнав
плот, лодка возвращается обратно. Найдите
сумму всех возможных значений ,
при которых к моменту возвращения лодки
к пристани
,
при которых к моменту возвращения лодки
к пристани плот пройдет более 18 км.
плот пройдет более 18 км.
РТ3 2012
В12.Три бригады должны выполнить
работу. Первая бригада делает в день
200 деталей, вторая на деталей меньше, а третья — на
деталей меньше, а третья — на деталей больше, чем первая. Сначала
первая и вторая бригады, работая вместе,
выполняют
деталей больше, чем первая. Сначала
первая и вторая бригады, работая вместе,
выполняют всей работы, затем все три бригады,
работая вместе, выполняют оставшуюся
часть работы. При каком значении
всей работы, затем все три бригады,
работая вместе, выполняют оставшуюся
часть работы. При каком значении вся работа будет выполнена указанным
способом за наименьшее время?
вся работа будет выполнена указанным
способом за наименьшее время?
РТ
2 2011 В10. Из города
 выехал велосипедист, через 10 ч из города
выехал велосипедист, через 10 ч из города Навстречу ему выехал второй велосипедист.
При встрече оказалось, что первый
велосипедист проехал На 45 км больше
второго. Продолжая путь с той же скоростью
и без остановок, второй велосипедист
прибыл в
Навстречу ему выехал второй велосипедист.
При встрече оказалось, что первый
велосипедист проехал На 45 км больше
второго. Продолжая путь с той же скоростью
и без остановок, второй велосипедист
прибыл в через 72 ч после встречи, а первый
велосипедист в
через 72 ч после встречи, а первый
велосипедист в —
через 8 ч после встречи. Определите
скорость (в км/ч) второго велосипедиста.
—
через 8 ч после встречи. Определите
скорость (в км/ч) второго велосипедиста.
РТ 3 2011 В11. Два тела, находясь на расстоянии 600 м, начали двигаться навстречу друг другу. Первое проходит 9 м в секунду. Второе в первую секунду прошло 3 м, а в каждую следующую секунду проходит на 4 м больше, чем в предыдущую. Через сколько секунд два тела встретятся?
Решение
Обозначим
через
 — количество секунд, прошедших с момента
старта до встречи, тогда первое тело
прошло
— количество секунд, прошедших с момента
старта до встречи, тогда первое тело
прошло с.
Путь, пройденный вторым телом, за каждую
секунду представляет арифметическую
прогрессию, с первым членом — 3 и разностью
— 4, тогда путь, пройденный за
с.
Путь, пройденный вторым телом, за каждую
секунду представляет арифметическую
прогрессию, с первым членом — 3 и разностью
— 4, тогда путь, пройденный за с
равен
с
равен м.
Поскольку они встретились, то оба тела
в сумме прошли 600 м. Получаем уравнение:
м.
Поскольку они встретились, то оба тела
в сумме прошли 600 м. Получаем уравнение:





Первый корень, по физическому смыслу вводимой нами переменной, является посторонним.
Комментарий.При решении неявно подразумевалось (причем абсолютно необоснованно), что встреча произойдет через целое число секунд после начала движения.
Ответ:15.




 ,
,