
Текстовые задачи Задачи на работу (alldone)
РТ 2 2005 В3.Один комбайн убрал урожай с половины поля, а урожай с оставшейся части поля убрал второй комбайн, который работал быстрее первого. На всю работу ушло 12,5 часа. Работая вместе, они бы убрали это поле за 4 часа. Сколько часов нужно для уборки всего поля первому комбайну, если он работает один?
Решение
Iспособ
Пусть
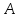 — весь объем работы,
— весь объем работы,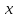 и
и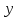 — производительности первого и второго
комбайна соответственно, тогда
— производительности первого и второго
комбайна соответственно, тогда — искомая величина. По условию задачи
составляем систему:
— искомая величина. По условию задачи
составляем систему: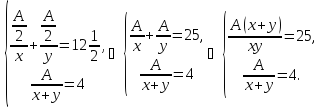
Умножим
первое уравнение на второе, получим
 По
условию
По
условию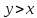 ,
следовательно,
,
следовательно,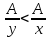 .Тогда
по теореме Виета
.Тогда
по теореме Виета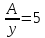 ,
,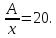
IIспособ
Обозначения
будем использовать те же, что и в первом
способе. Введем еще одно обозначение.
Пусть
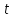 — время, за которое первый комбайн убрал
половину поля, тогда получает следующие
соотношения:
— время, за которое первый комбайн убрал
половину поля, тогда получает следующие
соотношения: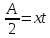 ,
,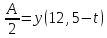 и
и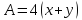 ,
а искомая величина равна
,
а искомая величина равна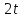 .
Тогда
.
Тогда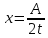 ,
,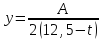 .
Подставим эти соотношения в третье
равенство, получим
.
Подставим эти соотношения в третье
равенство, получим или
или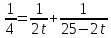 ,
откуда
,
откуда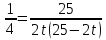 ,
следовательно,
,
следовательно,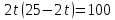 ,
откуда
,
откуда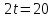 или
или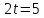 .
Так как второй комбайн работал быстрее,
то
.
Так как второй комбайн работал быстрее,
то и тогда
и тогда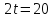 .
.
Ответ: 20.
ЦТ 2007 B8.Заказ по изготовлению деталей выполняется
на станках марок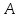 и
и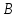 .
За 9 ч выполняют заказ 59 станков марки
.
За 9 ч выполняют заказ 59 станков марки и 36 станков марки
и 36 станков марки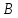 ,
а 13 станков марки
,
а 13 станков марки и 43 станка марки
и 43 станка марки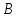 — за 18 ч. На сколько
процентов время выполнения заказа одним
станком марки
— за 18 ч. На сколько
процентов время выполнения заказа одним
станком марки меньше времени выполнения заказа одним
станком марки
меньше времени выполнения заказа одним
станком марки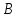 ?
?
Решение
Iспособ
Пусть
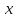 и
и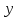 — время выполнения заказа одним станком
марки
— время выполнения заказа одним станком
марки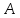 и
и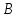 соответственно.
соответственно. — искомая величина. Пусть
— искомая величина. Пусть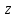 — объем всего заказа, тогда
— объем всего заказа, тогда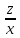 и
и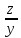 — производительности станков
соответствующих марок. Получаем систему
уравнений
— производительности станков
соответствующих марок. Получаем систему
уравнений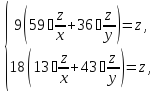 равносильную уравнению
равносильную уравнению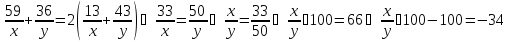 .
.
Знак минус
в ответ писать не надо, поскольку он
показывает, что время выполнения заказа
одним станком марки
 меньше времени выполнения заказа одним
станком марки
меньше времени выполнения заказа одним
станком марки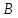 .
.
IIспособ
Пусть станок
марки
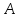 имеет производительность
имеет производительность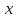 ,
а производительность станка марки
,
а производительность станка марки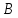 —
—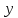 .
По условию задачи составим и решим
уравнение:
.
По условию задачи составим и решим
уравнение:

Известно,
что выполненная работа равна произведению
производительности на время. Примем
работу за 1, получим
 — время, за которое станок марки
— время, за которое станок марки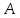 выполнил работу, а
выполнил работу, а — время за которое станок марки
— время за которое станок марки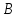 выполнил работу. Отвечая на вопрос
задачи, составляем и решаем пропорцию:
выполнил работу. Отвечая на вопрос
задачи, составляем и решаем пропорцию:
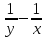 составляет
составляет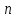 %,
%,
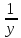 составляет 100%.
составляет 100%.
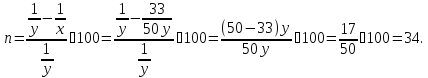
Значит,
время выполнения одним станком марки
 меньше времени выполнения заказа одним
станком марки
меньше времени выполнения заказа одним
станком марки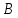 на 34 %.
на 34 %.
Ответ: 34.
РТ 2 2009 В4.При одновременной работе двух насосов разной мощности бассейн наполняется за 8ч. После ремонта насосов производительность первого из них увеличилась в 1,2 раза, а второго — в 1,6 раза, и при одновременной работе обоих насосов бассейн стал наполняться за 6 ч. За сколько минут наполняется бассейн при работе только первого насоса после ремонта?
Решение
Пусть
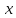 и
и — производительности первого и второго
насосов соответственно,
— производительности первого и второго
насосов соответственно, — объем всей работы, тогда искомая
величина равна
— объем всей работы, тогда искомая
величина равна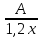 .
Получаем систему уравнений:
.
Получаем систему уравнений:

Домножим
первое уравнение на 1,6 и вычтет из него
второе, получим
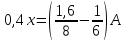 .
Домножим данное соотношение на З,
получим:
.
Домножим данное соотношение на З,
получим: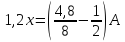 ,
откуда
,
откуда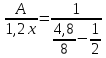 ,
, .
10 ч = 600 мин.
.
10 ч = 600 мин.
Ответ: 600.
Задачи на движение (alldone)
РТ 2004 В7.Первую четверть пути поезд двигался со скоростью 80 км/ч, а оставшуюся часть — со скоростью 60 км/ч. С какой средней скоростью двигался поезд?
Решение
Пусть
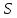 — длина всего пути, тогда время,
затраченное на поездку, равно
— длина всего пути, тогда время,
затраченное на поездку, равно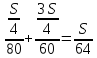 .
А средняя скорость равна
.
А средняя скорость равна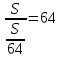 .
.
Ответ: 64.
ЦТ 2004 B9.Из пункта в пункт
в пункт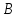 ,
расстояние между которыми 104 км, с
постоянной скоростью выезжает автобус.
Через 30 мин за ним выезжает мотоциклист
со скоростью 40 км/ч, который, догнав
автобус, возвращается обратно в пункт
,
расстояние между которыми 104 км, с
постоянной скоростью выезжает автобус.
Через 30 мин за ним выезжает мотоциклист
со скоростью 40 км/ч, который, догнав
автобус, возвращается обратно в пункт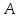 с прежней скоростью. Наибольшее целое
значение скорости (в километрах в час),
при котором автобус прибывает в пункт
с прежней скоростью. Наибольшее целое
значение скорости (в километрах в час),
при котором автобус прибывает в пункт раньше, чем мотоциклист возвращается
в пункт
раньше, чем мотоциклист возвращается
в пункт ,
равно…
,
равно…
Решение
I способ
Пусть
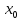 — скорость автобуса, при которой он
прибывает в пункт
— скорость автобуса, при которой он
прибывает в пункт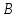 раньше мотоциклиста, возвращающегося
в пункт
раньше мотоциклиста, возвращающегося
в пункт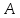 .
Тогда и при всех скоростях больших
.
Тогда и при всех скоростях больших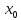 ,
но меньших 40 (иначе мотоциклист не
догонит), автобус прибудет раньше
мотоциклиста. Ограничение скорости
автобуса наложено в том факте, что
мотоциклист догнал автобус. Значит,
максимальное значение скорости автобуса
(
,
но меньших 40 (иначе мотоциклист не
догонит), автобус прибудет раньше
мотоциклиста. Ограничение скорости
автобуса наложено в том факте, что
мотоциклист догнал автобус. Значит,
максимальное значение скорости автобуса
(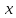 )
будет тогда, когда мотоциклист его
догонит в пункте
)
будет тогда, когда мотоциклист его
догонит в пункте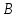 .
Получаем уравнение
.
Получаем уравнение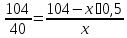 .
Откуда
.
Откуда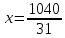 ,
,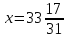 .
.
При данном
решении обязательно надо сделать
проверку, что при скорости 33 км/ч автобус
прибывает в пункт
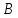 раньше, чем мотоциклист возвращается
в пункт
раньше, чем мотоциклист возвращается
в пункт .
.
Найдем
время, за которое мотоциклист догонит
автобус:
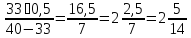 ч. Очевидно, что за это же время мотоциклист
вернется назад. Найдем время, за которое
автобус доедет в пункт
ч. Очевидно, что за это же время мотоциклист
вернется назад. Найдем время, за которое
автобус доедет в пункт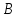 ,
после встречи с мотоциклистом:
,
после встречи с мотоциклистом: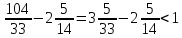 ч.
ч.
II способ
Пусть
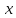 — скорость автобуса. Тогда
— скорость автобуса. Тогда — время, за которое мотоциклист догонит
автобус, за это же время, мотоциклист
вернется назад.
— время, за которое мотоциклист догонит
автобус, за это же время, мотоциклист
вернется назад.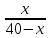 — время, за которое мотоциклист совершит
поездку.
— время, за которое мотоциклист совершит
поездку.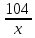 — время движения автобуса.
— время движения автобуса. — путь проделанный мотоциклистом до
встречи с автобусом. Получаем систему
— путь проделанный мотоциклистом до
встречи с автобусом. Получаем систему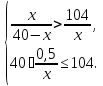 Решение первого неравенства системы:
Решение первого неравенства системы: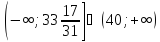 ,
,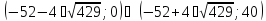 — решение второго неравенства, тогда
— решение второго неравенства, тогда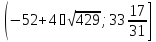 — решение системы. Поскольку,
— решение системы. Поскольку,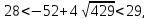 то 33 является ответом.
то 33 является ответом.
Ответ: 33.
РТ 2 2008 В9.Из поселка в одном и том же направлении выехали последовательно с интервалом в 1 час три велосипедиста. Так как первый из них двигался со скоростью 12 км/ч, второй — 10 км/ч, то третий велосипедист, имея более высокую скорость, догнал сначала второго велосипедиста, а еще через два часа первого. Запишите в ответе число, выражающее скорость (км/ч) третьего велосипедиста.
Решение
Пусть
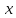 — скорость третьего велосипедиста,
тогда
— скорость третьего велосипедиста,
тогда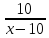 — время, за которое догонит третий
велосипедист второго, а
— время, за которое догонит третий
велосипедист второго, а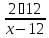 — время, за которое третий велосипедист
догонит первого. По условию задачи
получаем уравнение:
— время, за которое третий велосипедист
догонит первого. По условию задачи
получаем уравнение:
Откуда
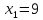 ,
что противоречит тому, что скорость
третьего велосипедиста самая большая,
и
,
что противоречит тому, что скорость
третьего велосипедиста самая большая,
и .
.
Ответ: 20.
РТ 1 2011 В10.Две автомашины выехали одновременно из одного и того же пункта в одном и том же направлении: одна — со скоростью 40 км/ч, а другая — 50 км/ч. Спустя полчаса из того же пункта в том же направлении выехала третья машина, которая обогнала сначала первую, а еще через 1 час 30 мин — вторую машину. Найдите скорость третьей машины.
Решается аналогично.
РТ 3 2008
В11.Из города в город
в город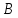 выезжает
велосипедист, а через 3 часа после его
выезда из города
выезжает
велосипедист, а через 3 часа после его
выезда из города выезжает навстречу мотоциклист, скорость
которого в 3 раза больше скорости
велосипедиста. К моменту встречи
велосипедист проехал половину пути до
выезжает навстречу мотоциклист, скорость
которого в 3 раза больше скорости
велосипедиста. К моменту встречи
велосипедист проехал половину пути до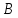 .
Если бы мотоциклист выехал не через 3,
а через 2 часа после велосипедиста, то
встреча произошла бы на 15 км ближе к
.
Если бы мотоциклист выехал не через 3,
а через 2 часа после велосипедиста, то
встреча произошла бы на 15 км ближе к .
Найдите расстояние между
.
Найдите расстояние между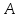 и
и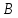 .
.
Решение
Пусть длина
пути от
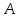 до
до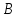 равна
равна ,
,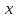 — скорость велосипедиста, тогда
— скорость велосипедиста, тогда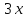 — скорость мотоциклиста,
— скорость мотоциклиста,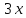 — путь проделанный велосипедистом до
выезда мотоциклиста,
— путь проделанный велосипедистом до
выезда мотоциклиста,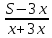 — время встречи велосипедиста и
мотоциклиста. Получаем уравнение:
— время встречи велосипедиста и
мотоциклиста. Получаем уравнение:
По аналогии
для случая „если бы… “ получаем:
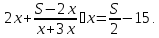
Объединяем эти уравнения в систему и приводим подобные:
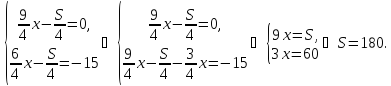
Комментарии. Если рассматривать движение мотоциклиста, то получаем следующую систему:
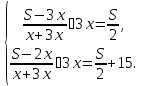
Ответ: 180.
ЦТ 2008 В10.Из двух городов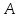 и
и одновременно навстречу друг другу с
постоянными скоростями выехали два
автомобиля. Первый автомобиль приехал
в город
одновременно навстречу друг другу с
постоянными скоростями выехали два
автомобиля. Первый автомобиль приехал
в город через 16 часов после встречи, а второй —
в город
через 16 часов после встречи, а второй —
в город через 25 часов после встречи. За какое
время первый автомобиль проезжает путь
от
через 25 часов после встречи. За какое
время первый автомобиль проезжает путь
от до
до ?
?
Решение
Iспособ
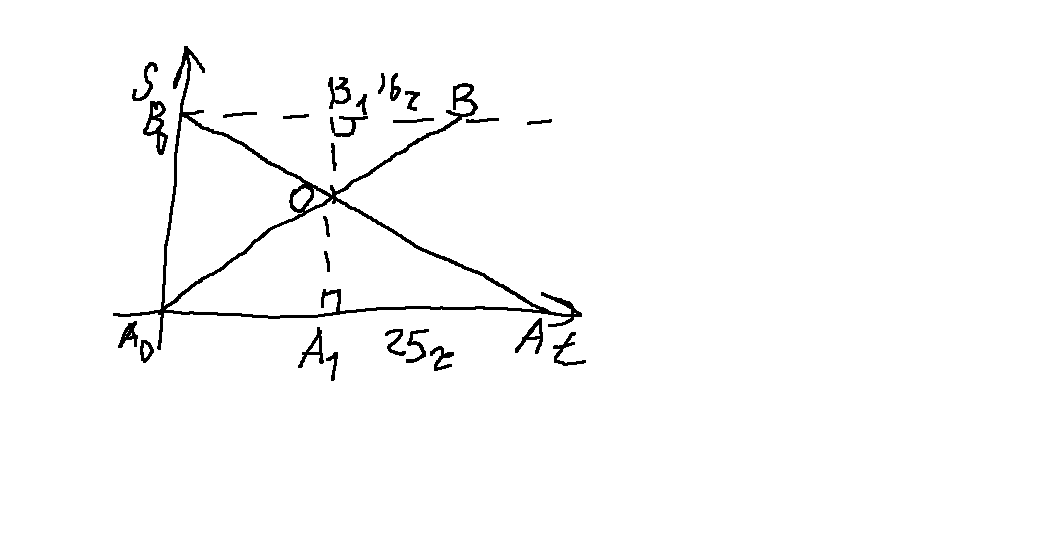
Изобразим
схематично, движение автомобилей на
координатной плоскости
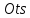 (время – пройденный путь). Из подобия
прямоугольных треугольников
(время – пройденный путь). Из подобия
прямоугольных треугольников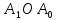 ,
,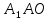 и
и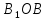 имеем, что
имеем, что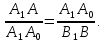 Пусть до встречи автомобили проехали
Пусть до встречи автомобили проехали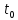 часов, тогда
часов, тогда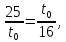
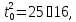
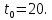
Значит, первый автомобиль проезжает путь за 20+16 часов.
IIспособ
Пусть
скорость первого автомобиля равна
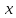 км/ч, скорость второго
км/ч, скорость второго км/ч, а время до встречи равно
км/ч, а время до встречи равно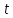 .
.
Рассмотрим рисунок.
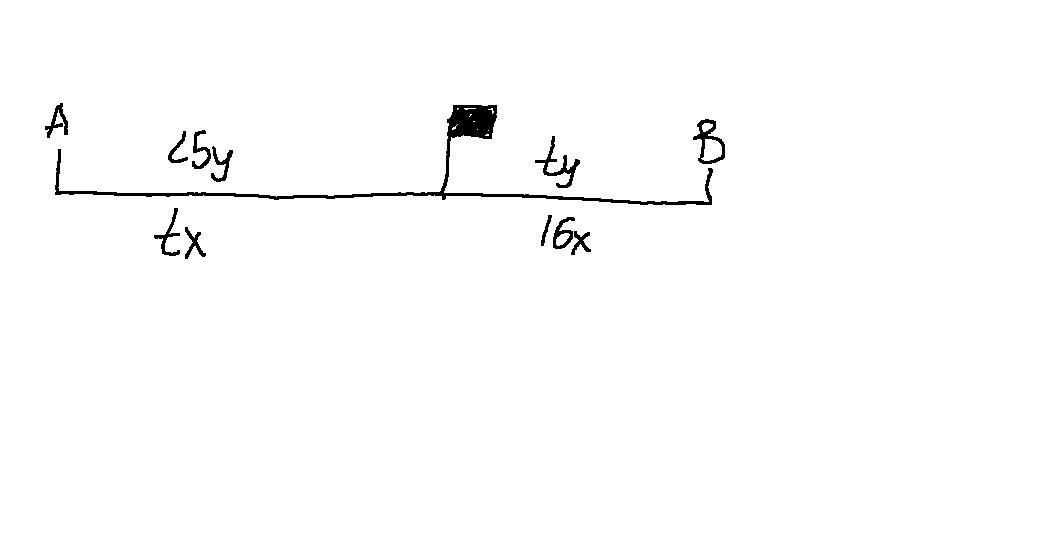
Составим
пропорцию:
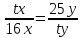 ,
,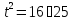 ,
,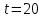 .
То есть до встречи оба автомобиля ехали
по 20 часов. Тогда 20+16 часов затратил
первый автомобиль на путь от
.
То есть до встречи оба автомобиля ехали
по 20 часов. Тогда 20+16 часов затратил
первый автомобиль на путь от до
до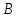 .
.
IIIспособ
Пусть
 (где
(где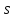 — весь путь от
— весь путь от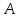 до
до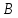 ,
,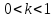 )
часть пути, который прошел первый
автомобиль до встречи. Тогда второй до
встречи прошел
)
часть пути, который прошел первый
автомобиль до встречи. Тогда второй до
встречи прошел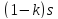 часть пути. Так как первый автомобиль
приехал в город
часть пути. Так как первый автомобиль
приехал в город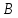 через 16 часов после встречи, то его
скорость равна
через 16 часов после встречи, то его
скорость равна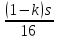 ,
а второй — в город
,
а второй — в город через 25 часов после встречи, то его
скорость равна
через 25 часов после встречи, то его
скорость равна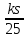 .
Найдем время, за которое автомобили
пройдут все расстояние. Первый:
.
Найдем время, за которое автомобили
пройдут все расстояние. Первый: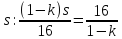 .
Второй:
.
Второй: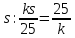 .
.
Так как
первый автомобиль приехал в город
 через 16 часов после встречи, а второй —
через 25 часов после встречи, то составим
и решим уравнение
через 16 часов после встречи, а второй —
через 25 часов после встречи, то составим
и решим уравнение
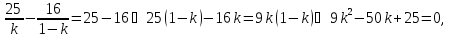
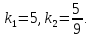
Так как
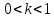 ,
то при
,
то при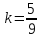 находим время, за которое первый
автомобиль проезжает путь от до т.е.
находим время, за которое первый
автомобиль проезжает путь от до т.е.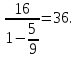
Ответ: 36.
РТ 1 2009
В10.Поезд идет по расписанию из
города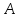 в город
в город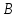 14 ч. Проехав некоторую часть пути, поезд
снизил скорость в 2 раза и поэтому прибыл
в
14 ч. Проехав некоторую часть пути, поезд
снизил скорость в 2 раза и поэтому прибыл
в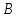 с опозданием на 7 ч. Если бы поезд до
снижения скорости проехал на 300 км
больше, то опоздание составило бы 4 ч.
Найдите расстояние в км между городами.
с опозданием на 7 ч. Если бы поезд до
снижения скорости проехал на 300 км
больше, то опоздание составило бы 4 ч.
Найдите расстояние в км между городами.
Решение
Iспособ
Пусть
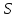 — расстояние между городами,
— расстояние между городами,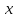 — первоначальная скорость поезда,
— первоначальная скорость поезда,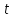 — время, когда поезд снизил скорость.
В задаче описаны три ситуации. В каждой
ситуации выразим путь, получим систему
из 3 уравнений:
— время, когда поезд снизил скорость.
В задаче описаны три ситуации. В каждой
ситуации выразим путь, получим систему
из 3 уравнений:
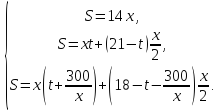
Раскроем
скобки и вычтем из второго уравнение
третье, получим уравнение
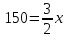 ,
откуда
,
откуда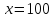 ,
,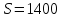 .
.
IIспособ
Пусть
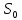 — расстояние, которое прошел поезд,
перед тем, как снизить скорость. По
аналогии с первым способом, для каждой
ситуации выразим затраченное время:
— расстояние, которое прошел поезд,
перед тем, как снизить скорость. По
аналогии с первым способом, для каждой
ситуации выразим затраченное время:

Разобьем
в третьем уравнении каждую дробь на два
слагаемых так, чтобы одно из них совпадало
с дробью из второго уравнения, и вычтем
из второго уравнения третье, получим
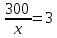 ,
,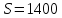 .
.
Ответ: 1400.
РТ 2 2010 В12.Три автомобиля двигаются по шоссе в одну сторону с постоянными скоростями. Когда впервые два из них находились в одной точке, третий был на расстоянии 30 км позади них. Когда третий автомобиль догнал второй, первый отстал от них на 6 км. Найдите расстояние (в км) между первым и вторым автомобилями в тот момент, когда первый и третий находились в одной точке.
Решение
Iспособ
Из условия задачи следует, что когда третий автомобиль догнал второго, он продвинулся относительно первого на 36 км, ликвидировав отставание в 30 км и обогнав его на 6 км. За это время второй автомобиль продвинулся относительно первого на 6 км. Следовательно, относительная скорость третьего автомобиля по отношению к первому вшестеро больше относительной скорости второго автомобиля по отношению к первому. Таким образом, когда третий автомобиль ликвидирует отставание от первого в 30 км, второй автомобиль обгонит первого на 5 км.
Iaспособ
Пусть
скорости первой, второй и третьей машины
равны
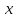 ,
,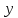 и
и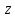 км/ч. Тогда время, за которое третья
машина догонит вторую равно
км/ч. Тогда время, за которое третья
машина догонит вторую равно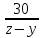 .
Это время равно времени, за которое
первый автомобиль отстанет от второго
на 6 км, то есть
.
Это время равно времени, за которое
первый автомобиль отстанет от второго
на 6 км, то есть .
За это же время расстояние между третьим
и вторым сократилось с 30 км до 0, а после
этого увеличилось до 6 км, т.е.
.
За это же время расстояние между третьим
и вторым сократилось с 30 км до 0, а после
этого увеличилось до 6 км, т.е.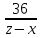 .
Имеем
.
Имеем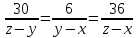 .
Чтобы найти расстояние между вторым и
первым автомобилями в тот момент, когда
третий и первый находились в одной
точке, можно из расстояния, на которое
успел отъехать второй, вычесть расстояние,
которое за то же время прошел первый.
Время, за которое третий догнал первый,
равно
.
Чтобы найти расстояние между вторым и
первым автомобилями в тот момент, когда
третий и первый находились в одной
точке, можно из расстояния, на которое
успел отъехать второй, вычесть расстояние,
которое за то же время прошел первый.
Время, за которое третий догнал первый,
равно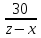 .
За это время второй прошел
.
За это время второй прошел км, а первый —
км, а первый —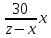 км. Таким образом, ответ дает выражение
км. Таким образом, ответ дает выражение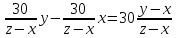 .
Из уравнения
.
Из уравнения выразим
выразим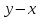 ,
а из
,
а из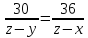 выразим
выразим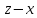 .
После сокращения дроби получим, что
.
После сокращения дроби получим, что .
.
IIспособ
Треугольник
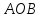 подобен треугольнику
подобен треугольнику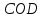 ,
следовательно,
,
следовательно,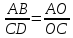 ,
,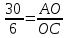 ,
, .
.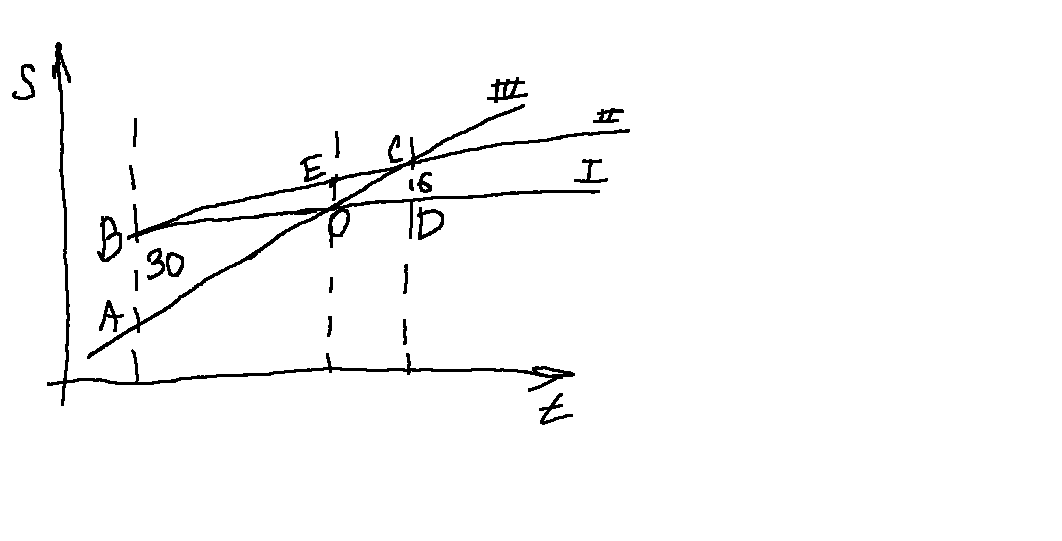
Треугольник
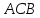 подобен треугольнику
подобен треугольнику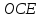 ,
следовательно,
,
следовательно, ,
, ,
,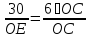 ,
,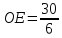 .
.
IIIспособ
Пусть
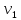 ,
,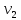 ,
, — скорости первого, второго и третьего
автомобиля,
— скорости первого, второго и третьего
автомобиля,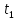 ,
,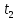 — моменты времени, когда произошли
встречи третьего и первого, второго и
третьего автомобилей соответственно.
Получаем равенства:
— моменты времени, когда произошли
встречи третьего и первого, второго и
третьего автомобилей соответственно.
Получаем равенства: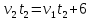 ,
,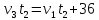 ,
,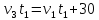 .
Из них получаем:
.
Из них получаем: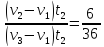 ,
откуда
,
откуда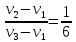 .
Поскольку надо найти
.
Поскольку надо найти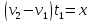 ,
то имеем
,
то имеем ,
то есть
,
то есть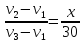 ,
окончательно,
,
окончательно,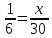 ,
то есть
,
то есть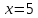 .
.
IIIа способ
Пусть
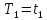 ,
,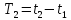 ,
тогда
,
тогда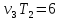 ,
, ,
,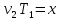 ,
,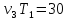 .
Получаем
.
Получаем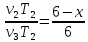 ,
,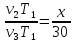 .
В каждом из равенств сокращаем время,
имеем
.
В каждом из равенств сокращаем время,
имеем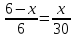 .
.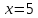 .
.
Ответ: 5.
РТ 3 2005 В9.Рыболов, охотник и грибник идут в одном направлении с постоянными скоростями. Когда рыболов и охотник находились в одной точке, грибник отставал от них на 220м. Когда грибник догнал охотника, рыболов отставал от них на 180м. Найдите расстояние (м) между охотником и рыболовом, в тот момент, когда грибник и рыболов находились в одной точке.
Решение аналогично задаче выше. Ответ: 99.
