
- •1.Пространство rⁿ
- •2.Метрическое пространство, евклидово пространство.
- •3.Основные или важнейшие множества точек пространства
- •4.Функции n-переменных.
- •5.Сходимость в пространтсве Rn.
- •6.Предел функции нескольких переменных.
- •8.Повторные пределы.
- •9.Непрерывность функции нескольких переменных.
- •10.Непрерывность функции нескольких
- •11. Основрые свойства непрерывных функций нескольких переменных
- •12. Частные производные ф-ии нескольких переменных
- •13. Дифференцируемость ф-ии нескольких переменных
- •14. Дифференциал функции нескольких переменных
- •15. Достаточное условие дифференцируемости ф-ии нескольких переменных
- •16. Дифференцирование сложной ф-ии
- •17. Однородная функция. Теорема эйлера об однородных функциях
- •18. Инвариантность формы первого дифференциала функции нескольких переменных
- •19. Геометрический смысл дифференциуемости функции двух переменных
- •20. Производная по направлению
- •21.Частные производные высшего порядка.
- •22.Теорема о равенстве смешанных производных второго порядка ф-ции двух переменных.
- •23.Производные высших порядков.
- •26. Экстремум функции многих переменных.
- •27.Достаточные услов локальн экстрем ф-ций нескол перемен.
- •28. Критерий Сильвестра
- •29.Определение наибольшего и наименьшего значения
- •30.Не явные ф-ции.
- •31.Теорема о существ и диф-ти неявной ф-ции.
- •32.Вычисление частных производн неявно заданных ф-ций.
- •33.Неявные ф-ции определ систем функцион уравнений.
- •34. Зависимость ф-и нескольких переменных
- •35.Функциональные матрици
- •36. Усл.Экстремум
- •37.Метод неопредёлённых множетелей Логранжа.
- •38.Числовой ряд. Сходимость, расходимость рядов.
- •39.Необход признак сходим ряда.
- •40. Признак сравнения рядов
- •41.Признак Даламбера.
- •42.Признак Коши.
- •43. Интегральный признак Коши
- •44. Признак Лейбница
- •45. Абсолютная сходимость рядов
- •46. Признаки Дирихле и Абеля
- •47.Функциональные последовательности и ряды.
- •48.Равномерная сходимость функциональных рядов.
- •49.Свойства равном сходящ функции рядов.
- •50.Степенные ряды.
- •53.Ряд Фурье для четн. И нечетн. Ф-ий:
- •54.Ряд Фурье для ф-ций заданных на отрезке .
- •55.Криволинейный интеграл I рода:
- •56.Сведение криволинейного интеграла первого рода к определенному.
- •57.Криволинейный интеграл II рода:
- •59.Случай замкнутого контура:
- •61Cвязьмежду криволинейными интегралами 1-го и 2-го рода
- •62 Условия независимости криволинейного интеграла 2 рода от пути интегрирования.
- •63.Признак полоного диф-ла.
- •64.Вычисление криволинейного интеграла через первообразную
- •65Криволинейный интеграл 2-го рода
- •66 Двойной интеграл
- •67Сведение
- •68 Условие существования
- •69 Основные св-ва 2ного интеграла
- •70Замена переменных в двойном интеграле. Общий случай криволинейных координат
- •71. Формула Грина
- •72. Приложения двойных интегралов.
- •74 Определение и свойства тройного интеграла
- •75 Вычисление тройного интеграла.
- •76 Замена переменных в тройном интеграле.
- •77. Многократные интегралы.
- •80.Вычисление площади поверхности
- •85.Скалярное и векторное поля.
- •88.Циркуляция
- •90.Ротор.
- •92.Интеграл Дирихле.
- •93.Признак Дини сходимости тригонометрического ряда Фурье.
- •94.Признаки Дини, Липшица равномерной сходимости рядов Фурье.
- •96. Комплексная форма тригонометрического ряда Фурье.
- •97.Преобразования Фурье
- •98.Cвойства преобразования Фурье.
20. Производная по направлению
Для
простоты рассмотрим ф-ию 3-х переменных
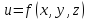 .
Предположим, что эта ф-ия определена в
некоторой окрестности точки
.
Предположим, что эта ф-ия определена в
некоторой окрестности точки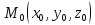 пространства
пространства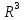 и дифференцируема в точке
и дифференцируема в точке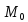 .
рассмотрим всевозможные лучи, выходящие
из точки
.
рассмотрим всевозможные лучи, выходящие
из точки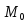 .
каждый такой луч задает единственный
вектор
.
каждый такой луч задает единственный
вектор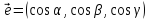 и определяет некоторое направление.
Зафиксируем некоторый луч, выходящий
из точки
и определяет некоторое направление.
Зафиксируем некоторый луч, выходящий
из точки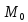 и определяющий некоторое направление,
заданное вектором
и определяющий некоторое направление,
заданное вектором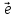 .
Возьмем на прямой, содержащей этот луч
производную отличную от точки
.
Возьмем на прямой, содержащей этот луч
производную отличную от точки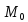 точку
точку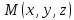 и рассмотрим вектор
и рассмотрим вектор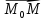 .
Пусть
.
Пусть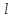 длина этого вектора
длина этого вектора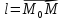 .
Т.к. вектор
.
Т.к. вектор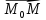 имеет коор-ты
имеет коор-ты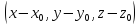 с одной стороны и коор-ты (
с одной стороны и коор-ты (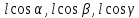 ),
то получим
),
то получим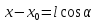 ,
,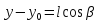 ,
,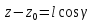
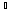
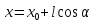 ,
,
,
,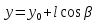 ,
,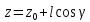
Эти
рав-ва показывают, что на прямой,
проходящей через точку
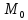 и определенной единичным вектором
и определенной единичным вектором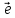 ф-ия
ф-ия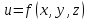 представляет собой сложную ф-ию одной
независимой переменной
представляет собой сложную ф-ию одной
независимой переменной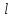 вида
вида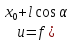 ,
,
,
,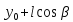 ,
,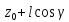 )
)
ОПРЕДЕЛЕНИЕ
Производная
указанной сложной ф-ии по переменной
 ,
взятая в точке
,
взятая в точке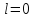 наз производной ф-ии
наз производной ф-ии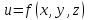 по направлению, определяемому единичным
вектором
по направлению, определяемому единичным
вектором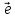 и обозначается
и обозначается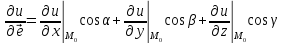
21.Частные производные высшего порядка.
Пусть задана функция 2х переменных z=f(x,y),найдем ее частные производные.
z/x=fx(x,y)
z/y=fy(x,y)
В общем случае, эти производные также являются функциями 2х и можно искать их частные производные. При этом получаем часные производные 2-ого и более порядков.Производные, в которых дифференцирование производится по разным переменным, называются смешанными.
Теорема: О независимости часных производных от порядка (последовательности) дифференцирования.
Две смешанные частные роизводные одного порядка, отличающиеся только порядком диф-я равны.
2z/xy=2z/yx - в следствии этого, при обозначении смешанных частных производных последовательность диф-я не указывается.
nz/xn-2y2
22.Теорема о равенстве смешанных производных второго порядка ф-ции двух переменных.
т.о.
понят частн производ n-порядка ввод
по идукции, переходя от первой частн
произв к последующим,соотнош определ
частн произв n-го порядка по x1i,x2i…xn-1i
имеет вид: если не все индексы i1,i2…in совпад между
собой, то частн производ n-го порядка
наз смешанной производ n-го порядка.
Замач: т.к. частн произв ф-ции u по аргум
xi опрел как обыкнов произв ф-ции одной
перемен xi, при фиксир знач остал
перемен,то вычисл частн произв высших
поряд производится по правилам вычисл
обыкнов произв первого порядка. Опред:
ф-ция u= f(x1,x2…xn) наз n-раз дифференц в
точке М0
если не все индексы i1,i2…in совпад между
собой, то частн производ n-го порядка
наз смешанной производ n-го порядка.
Замач: т.к. частн произв ф-ции u по аргум
xi опрел как обыкнов произв ф-ции одной
перемен xi, при фиксир знач остал
перемен,то вычисл частн произв высших
поряд производится по правилам вычисл
обыкнов произв первого порядка. Опред:
ф-ция u= f(x1,x2…xn) наз n-раз дифференц в
точке М0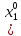 ,
,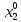 …
…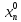 )
если все её частн произв порядка n-1 явл
дифференц в этой точке ф-циями. Из
определ след, что если u= f(x1,x2…xn) n-раз
дифференц в М0, то при n>1её частн произв
первого порядка n-1-раз дифференц в точке
М0, при n>2 любая её частная произв
второго порядека n-2 раза диференц в
точке М0 и т.д. Теор: для того что бы ф=ция
u= f(x1,x2…xn) была n-раз дифференц в М0,
достат чтобы все её частн производн
n-порядка были непрерыв в точке М0. Теор:
пусть ф-ция u=f(x,y) дважды дифференц в
точке М0(х0,y0), тогда в этой точке частн
произв:
)
если все её частн произв порядка n-1 явл
дифференц в этой точке ф-циями. Из
определ след, что если u= f(x1,x2…xn) n-раз
дифференц в М0, то при n>1её частн произв
первого порядка n-1-раз дифференц в точке
М0, при n>2 любая её частная произв
второго порядека n-2 раза диференц в
точке М0 и т.д. Теор: для того что бы ф=ция
u= f(x1,x2…xn) была n-раз дифференц в М0,
достат чтобы все её частн производн
n-порядка были непрерыв в точке М0. Теор:
пусть ф-ция u=f(x,y) дважды дифференц в
точке М0(х0,y0), тогда в этой точке частн
произв: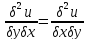 равны между собой.Данная теорем
утверж,что М0(х0,y0), имеет месть рав:
равны между собой.Данная теорем
утверж,что М0(х0,y0), имеет месть рав: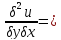 ,
если в этой точке дифференц ф-ции:
,
если в этой точке дифференц ф-ции: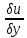 однако указан равенство имеет место
и при услов сущ произ:
однако указан равенство имеет место
и при услов сущ произ: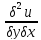 ;
;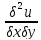 ;
но при дополнит требов непрер этих
произ в указанной точке. Теор:пусть в
некотор окрестн точки М0(х0,y0) ф-ции
u=f(x,y) имеет: u’x,u’y, uxy”, u”yx, пусть произв
: uxy”, u”yx, непрер в М0, тогда в этой точке:
: uxy”= u”yx,. Теор: пусть ф-ция u= f(x1,x2…xn)
n-раз дифферен в точке М0
;
но при дополнит требов непрер этих
произ в указанной точке. Теор:пусть в
некотор окрестн точки М0(х0,y0) ф-ции
u=f(x,y) имеет: u’x,u’y, uxy”, u”yx, пусть произв
: uxy”, u”yx, непрер в М0, тогда в этой точке:
: uxy”= u”yx,. Теор: пусть ф-ция u= f(x1,x2…xn)
n-раз дифферен в точке М0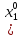 ,
,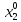 …
… )
тогда в этой точке знач любой смешан
частной произв n-го рорядка не зав от
того в каком порядке производится
последов диференц. Замеч: в случае n-раз
диференц ф-ции u= f(x1,x2…xn) любую частн
производ n-порядка, можно запис виде:
)
тогда в этой точке знач любой смешан
частной произв n-го рорядка не зав от
того в каком порядке производится
последов диференц. Замеч: в случае n-раз
диференц ф-ции u= f(x1,x2…xn) любую частн
производ n-порядка, можно запис виде: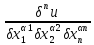 , где
, где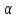 1,
1,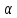 2….
2….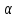 n-целые
числаудовл услов:
n-целые
числаудовл услов: =n.
=n.
