
- •1.Пространство rⁿ
- •2.Метрическое пространство, евклидово пространство.
- •3.Основные или важнейшие множества точек пространства
- •4.Функции n-переменных.
- •5.Сходимость в пространтсве Rn.
- •6.Предел функции нескольких переменных.
- •8.Повторные пределы.
- •9.Непрерывность функции нескольких переменных.
- •10.Непрерывность функции нескольких
- •11. Основрые свойства непрерывных функций нескольких переменных
- •12. Частные производные ф-ии нескольких переменных
- •13. Дифференцируемость ф-ии нескольких переменных
- •14. Дифференциал функции нескольких переменных
- •15. Достаточное условие дифференцируемости ф-ии нескольких переменных
- •16. Дифференцирование сложной ф-ии
- •17. Однородная функция. Теорема эйлера об однородных функциях
- •18. Инвариантность формы первого дифференциала функции нескольких переменных
- •19. Геометрический смысл дифференциуемости функции двух переменных
- •20. Производная по направлению
- •21.Частные производные высшего порядка.
- •22.Теорема о равенстве смешанных производных второго порядка ф-ции двух переменных.
- •23.Производные высших порядков.
- •26. Экстремум функции многих переменных.
- •27.Достаточные услов локальн экстрем ф-ций нескол перемен.
- •28. Критерий Сильвестра
- •29.Определение наибольшего и наименьшего значения
- •30.Не явные ф-ции.
- •31.Теорема о существ и диф-ти неявной ф-ции.
- •32.Вычисление частных производн неявно заданных ф-ций.
- •33.Неявные ф-ции определ систем функцион уравнений.
- •34. Зависимость ф-и нескольких переменных
- •35.Функциональные матрици
- •36. Усл.Экстремум
- •37.Метод неопредёлённых множетелей Логранжа.
- •38.Числовой ряд. Сходимость, расходимость рядов.
- •39.Необход признак сходим ряда.
- •40. Признак сравнения рядов
- •41.Признак Даламбера.
- •42.Признак Коши.
- •43. Интегральный признак Коши
- •44. Признак Лейбница
- •45. Абсолютная сходимость рядов
- •46. Признаки Дирихле и Абеля
- •47.Функциональные последовательности и ряды.
- •48.Равномерная сходимость функциональных рядов.
- •49.Свойства равном сходящ функции рядов.
- •50.Степенные ряды.
- •53.Ряд Фурье для четн. И нечетн. Ф-ий:
- •54.Ряд Фурье для ф-ций заданных на отрезке .
- •55.Криволинейный интеграл I рода:
- •56.Сведение криволинейного интеграла первого рода к определенному.
- •57.Криволинейный интеграл II рода:
- •59.Случай замкнутого контура:
- •61Cвязьмежду криволинейными интегралами 1-го и 2-го рода
- •62 Условия независимости криволинейного интеграла 2 рода от пути интегрирования.
- •63.Признак полоного диф-ла.
- •64.Вычисление криволинейного интеграла через первообразную
- •65Криволинейный интеграл 2-го рода
- •66 Двойной интеграл
- •67Сведение
- •68 Условие существования
- •69 Основные св-ва 2ного интеграла
- •70Замена переменных в двойном интеграле. Общий случай криволинейных координат
- •71. Формула Грина
- •72. Приложения двойных интегралов.
- •74 Определение и свойства тройного интеграла
- •75 Вычисление тройного интеграла.
- •76 Замена переменных в тройном интеграле.
- •77. Многократные интегралы.
- •80.Вычисление площади поверхности
- •85.Скалярное и векторное поля.
- •88.Циркуляция
- •90.Ротор.
- •92.Интеграл Дирихле.
- •93.Признак Дини сходимости тригонометрического ряда Фурье.
- •94.Признаки Дини, Липшица равномерной сходимости рядов Фурье.
- •96. Комплексная форма тригонометрического ряда Фурье.
- •97.Преобразования Фурье
- •98.Cвойства преобразования Фурье.
16. Дифференцирование сложной ф-ии
Пусть
дана ф-яи
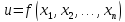
где
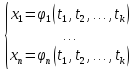 (1)
(1)
ТЕОРЕМА
Пусть
ф-ия (1) дифференцируема в некоторой
точке
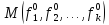 .
Пусть ф-ия
.
Пусть ф-ия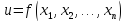 дифференцируема в соответствующей
точке
дифференцируема в соответствующей
точке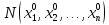 ,
где
,
где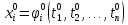 .
Тогда сложная ф-ия
.
Тогда сложная ф-ия ,
где
,
где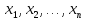 определены соотношениями (1), дифференцируема
в точке М. При этом частные производные
этой сложной ф-ии в точке М определяются
формулами:
определены соотношениями (1), дифференцируема
в точке М. При этом частные производные
этой сложной ф-ии в точке М определяются
формулами:
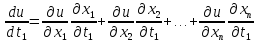
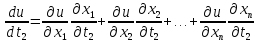
…
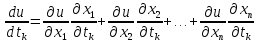
где
все частные производные
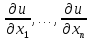 берутся в точке N, а все частные производные
берутся в точке N, а все частные производные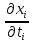 берутся в точке М, зависящей от t.
берутся в точке М, зависящей от t.
ЗАМЕЧАНИЕ
В
частном случае, когда ф-ии (1) зависят
только от одного аргумента t , получим
сложную ф-ию одной переменной t,т.е.
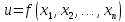 ,
где
,
где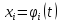 (i=1,2,…,n). В этом случае производная этой
сложной ф-ии определяется формулой
(i=1,2,…,n). В этом случае производная этой
сложной ф-ии определяется формулой
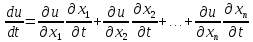
17. Однородная функция. Теорема эйлера об однородных функциях
ОПРЕДЕЛЕНИЕ
Ф-ия
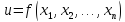 ,
заданная на множ-ве {M} наз однородной
ф-ей степени Р на этом множ-ве, если для
каждой т.
,
заданная на множ-ве {M} наз однородной
ф-ей степени Р на этом множ-ве, если для
каждой т.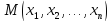 множ-ва {M} и для каждого числа t, для
которого
множ-ва {M} и для каждого числа t, для
которого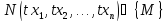 выполняется рав-во:
выполняется рав-во: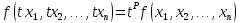
Пример:
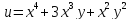
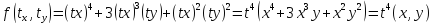
ТЕОРЕМА ЭЙЛЕРА(ОБ ОДНОРОДНОЙ Ф-ИИ)
Если
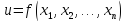 явл в некоторой области М дифференцируемой
однородной ф-ей степени Р, то в каждой
точке
явл в некоторой области М дифференцируемой
однородной ф-ей степени Р, то в каждой
точке области {M} справедливо рав-во:
области {M} справедливо рав-во:
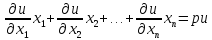 .
.
18. Инвариантность формы первого дифференциала функции нескольких переменных
Пусть
дана ф-ия
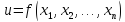 .
Если ф-ия
.
Если ф-ия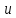 диф-ема и аргументы
диф-ема и аргументы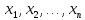 явл независимыми переменными, то
дифференциал этой ф-ии будет
явл независимыми переменными, то
дифференциал этой ф-ии будет
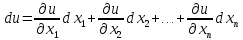
Предположим,
что это соотношение имеет место и в том
случае, когда аргументы
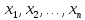 явл диф-ыми ф-ями переменных
явл диф-ыми ф-ями переменных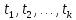 ,т.е.
,т.е.
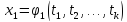
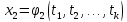
…
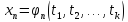
Указанные
свойства первого дифференциала обычно
наз инвариантностью его первой формы.
Пусть ф-ия
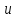 дифференцируема в точке
дифференцируема в точке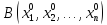 ,
а ф-ии
,
а ф-ии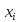 (i=1,2,…,n) дифференцируемы в точке
А
(i=1,2,…,n) дифференцируемы в точке
А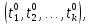 причем
причем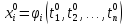 .
В этом случае ф-ию
.
В этом случае ф-ию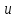 можно рассматривать как сложную ф-ию
независимых переменных
можно рассматривать как сложную ф-ию
независимых переменных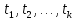 , которая в силу теоремы о дифференцируемости
сложной ф-ии будет диф-ема в точке А.
поэтому дифференциал duэтой сложной
ф-ии можно представить в виде
, которая в силу теоремы о дифференцируемости
сложной ф-ии будет диф-ема в точке А.
поэтому дифференциал duэтой сложной
ф-ии можно представить в виде
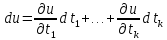 где
где
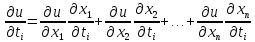 (i=1,2,…,k)
(i=1,2,…,k)
Представляя
эти соотношения в выражении для du и
собирая коэф-ты при
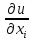 получим
получим
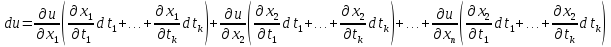
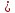
В
этом выражении
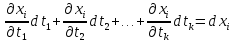 (i=1,2,…,n)
(i=1,2,…,n)
Поэтому получаем
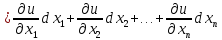
т.е. инвариантность формы первого дифференциала установлена.
Свойства
инвариантности формы первого дифференциала
позволяет установить следующие правила
для дифференциалов. Пусть
 дифференцируемые
ф-ии каких-либо переменных, тогда:
дифференцируемые
ф-ии каких-либо переменных, тогда:
1)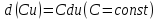
2)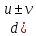 )
)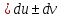
3)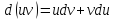
4)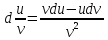
19. Геометрический смысл дифференциуемости функции двух переменных
В случае двух переменных условие дифференцируемости можно продемонстрировать геометрически.
ОПРЕДЕЛЕНИЕ
Плоскость
П, проходящая через точку
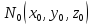 наз касательной плоскостью в этой
точке, если угол между этой плоскостью
и секущей, проходящей через точку
наз касательной плоскостью в этой
точке, если угол между этой плоскостью
и секущей, проходящей через точку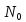 и любую точку
и любую точку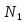 поверхности стремится к 0, когда точка
поверхности стремится к 0, когда точка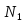 стремится к
стремится к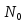 .
Если в точке
.
Если в точке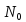 сущ касательная плоскость, то касательная
в точке
сущ касательная плоскость, то касательная
в точке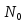 к любой кривой, расположенной на
поверхности и проходящей через точку
к любой кривой, расположенной на
поверхности и проходящей через точку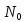 лежит в указанной плоскости. Покажем,
что из условия диф-сти ф-ии
лежит в указанной плоскости. Покажем,
что из условия диф-сти ф-ии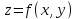 в точке
в точке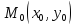 вытекает существование касательной
плоскости к графику этой ф-ии в точке
вытекает существование касательной
плоскости к графику этой ф-ии в точке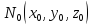 .
Пусть
.
Пусть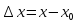 ,
,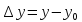 ,
,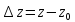 ,
где
,
где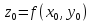 .
Условие дифференцируемости ф-ии
.
Условие дифференцируемости ф-ии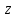 имеет вид
имеет вид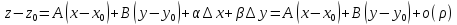 ,
где A и В постоянные равные частным
производным
,
где A и В постоянные равные частным
производным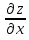 и
и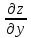 в точке
в точке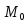 .
.
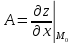 ,
B
,
B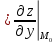 ,
,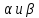 - б.м. при
- б.м. при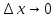 ,
,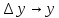 ф-ии
ф-ии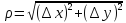 .
Рассм след ур-е
.
Рассм след ур-е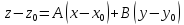 .
Из аналитической геометрии известно,
что это ур-е определяет в декартовой
системе коор-т некоторую плоскость,
проходящую через точку
.
Из аналитической геометрии известно,
что это ур-е определяет в декартовой
системе коор-т некоторую плоскость,
проходящую через точку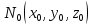 и имеющую нормальный вектор
и имеющую нормальный вектор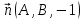 .
Покажем, что эта плоскость явл касательной
плоскостью в точке
.
Покажем, что эта плоскость явл касательной
плоскостью в точке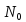 поверхности
поверхности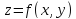 .
Действительно, эта плоскость проходит
через точку
.
Действительно, эта плоскость проходит
через точку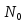 поверхности. Угол
поверхности. Угол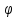 между нормальным вектором
между нормальным вектором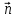 и любой секущей
и любой секущей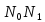
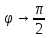 ,
когда точка
,
когда точка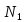 поверхности стремиться к точке
поверхности стремиться к точке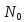 . Для этого найдем косинус
. Для этого найдем косинус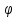
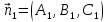
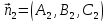
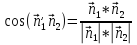
Найдем
коор-ты вектора
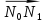 .
Еесли точка
.
Еесли точка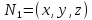 ,
то
,
то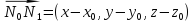 .
Поэтому
.
Поэтому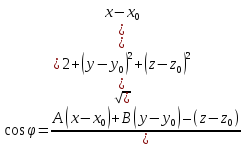 .
Поэтому из условия дифференцируемости
ф-ии
.
Поэтому из условия дифференцируемости
ф-ии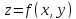 следует
следует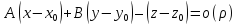 .
Поэтому
.
Поэтому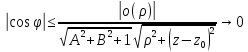 , когда
, когда
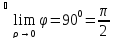
Т.о.
дифференцируемость ф-ии
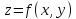 в точке
в точке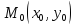 с геометрической точки зрения означает
наличие касательной плоскости к графику
ф-ии
с геометрической точки зрения означает
наличие касательной плоскости к графику
ф-ии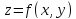 в точке
в точке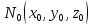 .
Т.к. коэф-ты А и В равны соотв-но частным
производным ф-ии
.
Т.к. коэф-ты А и В равны соотв-но частным
производным ф-ии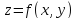 ,
вычисляемым в точке
,
вычисляемым в точке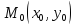 ,
то ур-е касательной плоскости может
быть записана в виде
,
то ур-е касательной плоскости может
быть записана в виде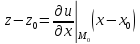 +
+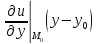
Нормальный
вектор
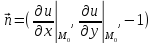 наз нормалью к поверхности
наз нормалью к поверхности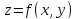 в точке
в точке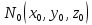 .
Ур-я нормали имеют вид
.
Ур-я нормали имеют вид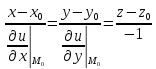 .
.
