
- •1.Пространство rⁿ
- •2.Метрическое пространство, евклидово пространство.
- •3.Основные или важнейшие множества точек пространства
- •4.Функции n-переменных.
- •5.Сходимость в пространтсве Rn.
- •6.Предел функции нескольких переменных.
- •8.Повторные пределы.
- •9.Непрерывность функции нескольких переменных.
- •10.Непрерывность функции нескольких
- •11. Основрые свойства непрерывных функций нескольких переменных
- •12. Частные производные ф-ии нескольких переменных
- •13. Дифференцируемость ф-ии нескольких переменных
- •14. Дифференциал функции нескольких переменных
- •15. Достаточное условие дифференцируемости ф-ии нескольких переменных
- •16. Дифференцирование сложной ф-ии
- •17. Однородная функция. Теорема эйлера об однородных функциях
- •18. Инвариантность формы первого дифференциала функции нескольких переменных
- •19. Геометрический смысл дифференциуемости функции двух переменных
- •20. Производная по направлению
- •21.Частные производные высшего порядка.
- •22.Теорема о равенстве смешанных производных второго порядка ф-ции двух переменных.
- •23.Производные высших порядков.
- •26. Экстремум функции многих переменных.
- •27.Достаточные услов локальн экстрем ф-ций нескол перемен.
- •28. Критерий Сильвестра
- •29.Определение наибольшего и наименьшего значения
- •30.Не явные ф-ции.
- •31.Теорема о существ и диф-ти неявной ф-ции.
- •32.Вычисление частных производн неявно заданных ф-ций.
- •33.Неявные ф-ции определ систем функцион уравнений.
- •34. Зависимость ф-и нескольких переменных
- •35.Функциональные матрици
- •36. Усл.Экстремум
- •37.Метод неопредёлённых множетелей Логранжа.
- •38.Числовой ряд. Сходимость, расходимость рядов.
- •39.Необход признак сходим ряда.
- •40. Признак сравнения рядов
- •41.Признак Даламбера.
- •42.Признак Коши.
- •43. Интегральный признак Коши
- •44. Признак Лейбница
- •45. Абсолютная сходимость рядов
- •46. Признаки Дирихле и Абеля
- •47.Функциональные последовательности и ряды.
- •48.Равномерная сходимость функциональных рядов.
- •49.Свойства равном сходящ функции рядов.
- •50.Степенные ряды.
- •53.Ряд Фурье для четн. И нечетн. Ф-ий:
- •54.Ряд Фурье для ф-ций заданных на отрезке .
- •55.Криволинейный интеграл I рода:
- •56.Сведение криволинейного интеграла первого рода к определенному.
- •57.Криволинейный интеграл II рода:
- •59.Случай замкнутого контура:
- •61Cвязьмежду криволинейными интегралами 1-го и 2-го рода
- •62 Условия независимости криволинейного интеграла 2 рода от пути интегрирования.
- •63.Признак полоного диф-ла.
- •64.Вычисление криволинейного интеграла через первообразную
- •65Криволинейный интеграл 2-го рода
- •66 Двойной интеграл
- •67Сведение
- •68 Условие существования
- •69 Основные св-ва 2ного интеграла
- •70Замена переменных в двойном интеграле. Общий случай криволинейных координат
- •71. Формула Грина
- •72. Приложения двойных интегралов.
- •74 Определение и свойства тройного интеграла
- •75 Вычисление тройного интеграла.
- •76 Замена переменных в тройном интеграле.
- •77. Многократные интегралы.
- •80.Вычисление площади поверхности
- •85.Скалярное и векторное поля.
- •88.Циркуляция
- •90.Ротор.
- •92.Интеграл Дирихле.
- •93.Признак Дини сходимости тригонометрического ряда Фурье.
- •94.Признаки Дини, Липшица равномерной сходимости рядов Фурье.
- •96. Комплексная форма тригонометрического ряда Фурье.
- •97.Преобразования Фурье
- •98.Cвойства преобразования Фурье.
36. Усл.Экстремум
Рассмотрим
функцию
 ,
, .
Будем считать, что ее аргументы являются
связанными между собой
.
Будем считать, что ее аргументы являются
связанными между собой
 (6.1)
(6.1)
Соотношения
(6.1) называются уравнениями связи Пусть
координаты точки
 удовлетворяют данной системе уравнений.
Говорят, что функция
удовлетворяют данной системе уравнений.
Говорят, что функция имеет в точке
имеет в точке условный минимум (максимум) при условиях
связи (6.1), если существует такая
условный минимум (максимум) при условиях
связи (6.1), если существует такая -окрестность
точки
-окрестность
точки ,
что для любой точки
,
что для любой точки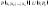 ,
, ,
координаты которой удовлетворяют
уравнениям (6.1), выполняется неравенство
,
координаты которой удовлетворяют
уравнениям (6.1), выполняется неравенство
 ).В
отличие от обычной (безусловной) точки
экстремума, значение функции в точке
условного экстремума сравнивается с
ее значениями не во всех точках некоторой
).В
отличие от обычной (безусловной) точки
экстремума, значение функции в точке
условного экстремума сравнивается с
ее значениями не во всех точках некоторой -окрестности
точки
-окрестности
точки ,
а только в тех ее точках, которые связаны
между собой условиями связи.
,
а только в тех ее точках, которые связаны
между собой условиями связи.
37.Метод неопредёлённых множетелей Логранжа.
Пусть
треб н-ти экстрем ф-ции u=f(x1..xn, y1..ym) при
налич услов связи Fi(x1..xn, y1..ym)=0 состав
ф-цию:
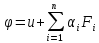 эту ф-цию наз ф-цией Лагранжа счит что
для
эту ф-цию наз ф-цией Лагранжа счит что
для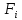 вып все услов сформулир ранее и что
ф-ция u дифференц, выберем множет
вып все услов сформулир ранее и что
ф-ция u дифференц, выберем множет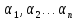 так чтобы выполн равенст:
так чтобы выполн равенст: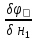 =0,
=0,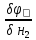 =0,
=0,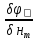 =0,
=0,
Это
можно сдел т.к. эти рав прив к систем
линейн уравнен: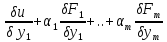 =0…
=0…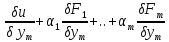 =0
определ которой:
=0
определ которой: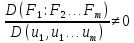 ,
потому дифференц ф-ции: d
,
потому дифференц ф-ции: d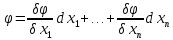 +
+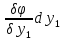 +…+
+…+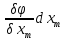 =
=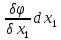 +..+
+..+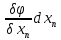 т.к. при сдел предпол перемен x1..xn явл
независ то отсюда:
т.к. при сдел предпол перемен x1..xn явл
независ то отсюда: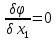 ,
,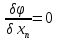 в резул для нах условн экстрем получ
сист n+2m уравн:
в резул для нах условн экстрем получ
сист n+2m уравн: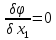 …
…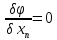 – n-уравн;
– n-уравн;
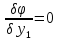 …
…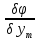 =0
– m-уравн;
=0
– m-уравн;
F1=0…Fm=0
–m- уравн.(*) решая эту ситем найд коорд
точек возможн экстрем и множет: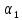 …
…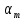 .
Предпол что в М0 вып необх услов условн
экстрем.Пусть ф-ции u1, F1,F2…Fm дважды
диференц в окрестн точки М0 и все частн
произв 2-го порядка непрер в М0. Из
построен ф-ции Лагранжа видно что при
нал услов связи (2) экстрем ф-ции u и ф-ции
Лагранжа совпад поэт для получ достат
услов в точке М0 ф-ци u при нал связей
след присоед к услов сис уравн (*), требов
знака определ в этой точке
.
Предпол что в М0 вып необх услов условн
экстрем.Пусть ф-ции u1, F1,F2…Fm дважды
диференц в окрестн точки М0 и все частн
произв 2-го порядка непрер в М0. Из
построен ф-ции Лагранжа видно что при
нал услов связи (2) экстрем ф-ции u и ф-ции
Лагранжа совпад поэт для получ достат
услов в точке М0 ф-ци u при нал связей
след присоед к услов сис уравн (*), требов
знака определ в этой точке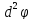 при этом в точке М0 будет минимум если
при налич связей:
при этом в точке М0 будет минимум если
при налич связей: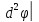 М0>0
услов min;
М0>0
услов min;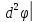 М0<0-max.
Замеч: второй дифференц
М0<0-max.
Замеч: второй дифференц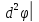 М0
можно вычисл так как если бы все перемен
x1..xn, y1..ym были незав в этом случ:
М0
можно вычисл так как если бы все перемен
x1..xn, y1..ym были незав в этом случ: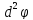 =(
=(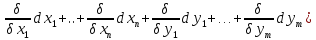 2
2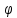 ..
..
38.Числовой ряд. Сходимость, расходимость рядов.
Пусть
 –
–
числовая последовательность. Выражение вида
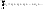
называется числовым рядом, числа
 ,
,
 ,
…,
,
…, ,
… – членами ряда, а
,
… – членами ряда, а
число
 –
– -м
или общим членом ряда.
-м
или общим членом ряда.
Сумма
конечного числа
 первых членов
первых членов
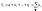
называется
 -й
частичной суммой данного ряда.
-й
частичной суммой данного ряда.
В частности,
 ,
,
 ,
,
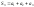 ,
,
……………………

………………………… .
Если
для последовательности
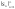
частичных
сумм ряда
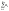 существует
существует
конечный
предел
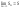 ,
то ряд
,
то ряд
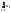 называется
сходящимся, а число
называется
сходящимся, а число
 –суммой
данного ряда:
–суммой
данного ряда:
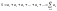 .
.
Если
предел последовательности

не существует или равен бесконечности,
то ряд называют расходящимся.
39.Необход признак сходим ряда.
Теор:
если ряд
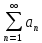 сход, то его n-член стрем к 0, при n
сход, то его n-член стрем к 0, при n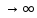 ,
тоесть
,
тоесть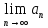 =0.Д-во:
рассмотр частичн суммы данного ряда:
Sn-1=a1+a2+..+an-1;
=0.Д-во:
рассмотр частичн суммы данного ряда:
Sn-1=a1+a2+..+an-1;
Sn-=a1+a2+..+an-1+an
т.к.
ряд
сход
то
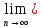 Sn-1=
Sn-1=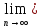 Sn-=S ,т.к.
an= Sn= Sn-1, то
Sn-=S ,т.к.
an= Sn= Sn-1, то
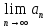 =
=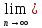 (Sn- Sn-1)=S-S=0.Следств:
n-член ряда не стрем к нулю при n
(Sn- Sn-1)=S-S=0.Следств:
n-член ряда не стрем к нулю при n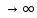 ,
то ряд расход:
,
то ряд расход: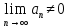 .
Расм ряд вида:
.
Расм ряд вида: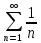 =1+
=1+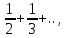 an=
an=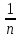 ,
,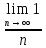 =0,
то данный ряд расход предпол что данный
ряд сход, тоесть:
=0,
то данный ряд расход предпол что данный
ряд сход, тоесть: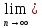 Sn=S,
Sn=S,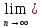 S2n=S,
S2n=S,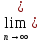 S2n-
Sn)=0 однако: S2n- Sn=
S2n-
Sn)=0 однако: S2n- Sn=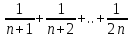 >
>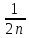 n=
n=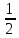 получ против, следов данный ряд расход,
этот ряд наз гармоническим.
получ против, следов данный ряд расход,
этот ряд наз гармоническим.
