Силы, действующие на заряженную частицу в электромагнитном поле. Сила Лоренца.

Мы уже знаем, что на проводник с током, помещенный в магнитное поле, действует сила Ампера. Но ток в проводнике – есть направленное движение зарядов. Отсюда напрашивается вывод, что сила, действующая на проводник с током в магнитном поле, обусловлена действием сил на отдельные движущиеся заряды, от которых это действие передается уже самому проводнику. Этот вывод подтверждается, в частности, еще и тем, что пучок свободно летящих заряженных частиц отклоняется магнитным полем.

Сила Ампера, действующая на элемент тока в магнитном поле с индукцией :

,

где α – угол между направлением тока в проводнике и вектором.

Пусть– скорость упорядоченного движения зарядов в проводнике;q – заряд носителя тока (в металлах q = - e). Для элемента тока можем написать:

dNq,

где n = dN/dV – концентрация зарядов, dN – число зарядов в элементе объема dV = Sdl. Тогда, сила, действующая в магнитном поле на один заряд, будет:

или в векторном виде.

Эту силу называют силой Лоренца (Lorentz H., 1853-1928).

Свойства силы Лоренца:

1. сила Лоренца действует только на движущуюся заряженную частицу;

2. и одновременно ;

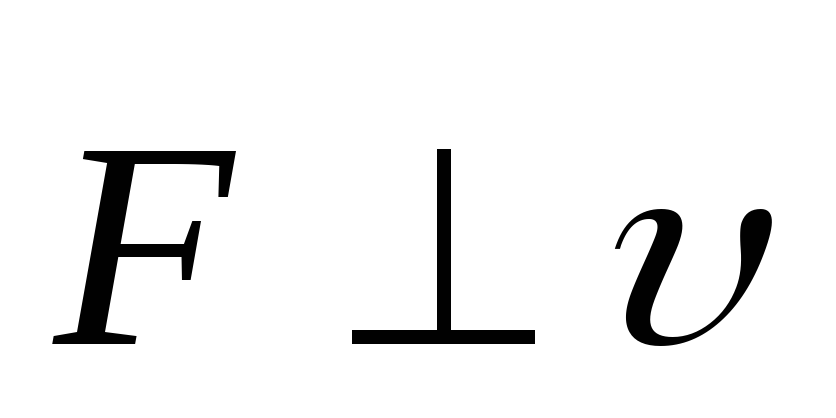3. поскольку , то сила Лоренцане совершает работу, а следовательно, не может изменить энергию частицы.

Полная сила, действующая на заряженную частицу в электромагнитном поле (которую также называют силой Лоренца) есть: .

4.3. Движение заряженной частицы в однородном постоянном магнитном поле.

В данном случае и сила Лоренца имеет только магнитную составляющую. Уравнением движения частицы, записанном в декартовой системе координат, в этом случае является:.

Рассмотрим сначала случай, когда частица влетает под прямым углом к силовым линиям магнитного поля (рис. 4.6.).

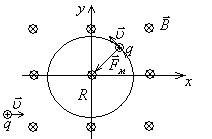
Рисунок 4.6. Движение заряженной частицы в магнитном поле ().

В системе координат, показанной на рисунке ,, и уравнение движения принимает вид:

,

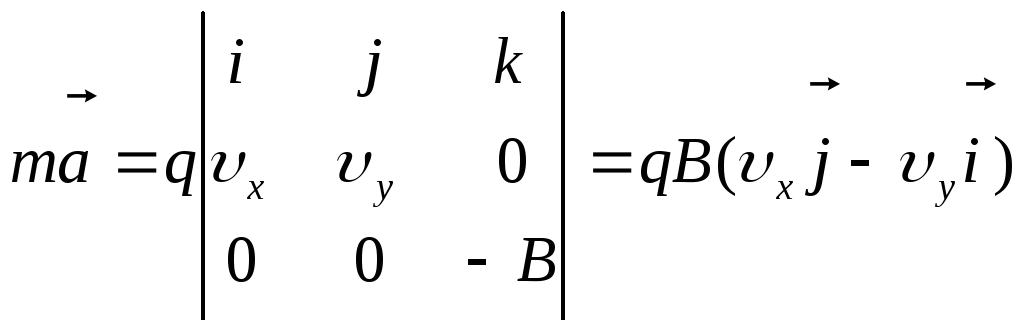откуда следует, что вектор полного ускорения частицы лежит в плоскости, перпендикулярной вектору. Легко убедиться также в том, что вектор ускоренияперпендикулярен вектору скорости частицыи составляет вместе с векторомправую тройку векторов (как и должно быть по свойствам силы Лоренца). Действительно,

.

Таким образом, ускорение частицы в каждый момент времени t направлено к центру кривизны траектории и играет роль нормального (центростремительного) ускорения. Модуль ускорения равен:

.

Траекторией движения является окружность, радиусR которой находим из условия: , то есть, откуда:.

Период обращения частицы

Отметим, что период обращения и соответственно угловая скорость движения частицы не зависят от линейной скорости .

Рассмотрим теперь случай, когда частица влетает под углом α к силовым линиям магнитного поля.

Рисунок 4.7. Общий случай движения заряженной частицы в однородном магнитном поле.

Разложим вектор скорости на две составляющие:- параллельную векторуи- перпендикулярную. Поскольку составляющая силы Лоренца в направленииравна нулю, она не может повлиять на величину. Что касается составляющей, то этот случай был рассмотрен выше. Таким образом, движение частицы можно представить как наложениедвух движений: одного – равномерного перемещения вдоль направления силовых линий поля со скоростью , второго –равномерного вращения в плоскости, перпендикулярной . В итоге траекторией движения будетвинтовая линия.

Шаг винтовой линии определяется по формуле: , где .Радиус витка находим по формуле:

Направление, в котором закручивается винтовая линия, зависит от знака заряда частицы. Если заряд частицы положительный, то винтовая линия закручивается против часовой стрелки, если смотреть вдоль направления , и наоборот –по часовой стрелке, если заряд частицы отрицательный.