
- •1. Основные определения и понятия термодинамики
- •2. Параметры состояния и уравнения состояния.
- •3.Термодинамическая и потенциальные работы, координаты p-V
- •4. Теплоемкость. Определение теплоемкости веществ.
- •5. Математическое выражение 1го начала термодинамики
- •6.Первое начало термодинамики по балансу рабочего тела
- •7. Аналитическое выражение первого начала термодинамики
- •8. Первое начало термодинамики для идеального газа.
- •9. Принцип существования энтропии идеального газа.
- •10. Процессы изменения состояния (изобара, изохора, изотерма и адибата)
- •11. Политропа с постоянным показателем.
- •12. Работа в термодинамических процессах простых тел (изобара, изохора, изотерма и адиабата)
- •13. Теплообмен в термодинамических процессах простых тел (изобара, изохора, изотерма и адиабата)
- •14. Процессы изменения состояния идеальных газов.
- •15. Работа и теплообмен в политропных процессах идеальных газов.
- •16. Круговые процессы. Кпд и холодильный коэффициент.
- •17. Обратимый цикл Карно.
- •18. Математическое выражение второго начала термостатики. Основные следствия.
- •19. Математическое выражение второго начала термодинамики. Основные следствия.
- •20. Смеси жидкостей, паров и газов, расчет характеристик смеси веществ. Схемы смещения.
- •21. Истечение жидкостей и газов. Основные расчётные соотношения.
- •22.Особенности истечения сжимаемой жидкости. Кризис истечения. Режимы истечения.
- •23.Переход через критическую скорость (сопло Лаваля).
- •24. Особенности истечения через каналы переменного сечения, сопло и диффузор.
- •25. Дросселирование. Эффект Джоуля-Томсона. Основные понятия
- •26. Процессы парообразования, определение параметров насушенного пара, диаграмма h-s.
- •27. Термодинамические циклы и кпд гту.
- •28.Термодинамические циклы и кпд поршневых двс.
- •29. Теплопроводность. Закон Фурье. Коэффициент теплопроводности
- •30. Дифференциальное уравнение теплопроводности. Условия однозначности
- •31. Теплопроводность через однослойные стенки (плоские, цилиндрические).
- •32 Теплопроводность через многослойные стенки (плоские, цилиндрические)
- •33.Теплоотдача. Закон Ньютона-Рихмана. Коэффициент теплоотдачи. Критериальные уравнения.
- •34. Теплообмен излучением. Основные законы.
- •35. Теплообмен излучением между телами.
- •36. Теплопередача. Основное уравнение теплопередачи. Коэффициент теплопроводности.
- •37. Теплопередача через плоскую однослойную и многослойную плоскую стенку
- •38. Теплопередача через криволинейные однослойные и многослойные стенки.
- •39.40. Оптимизация процессов теплопередачи. Способы интенсификации теплопередачи.
- •41,43. Теплопередача при переменных температурах. Средняя разность температур.
- •44. Расчет теплообменный аппаратов первого рода.
- •45. Расчет теплообменный аппаратов второго рода.
- •46. Паросиловые установки, цикл Ренкина, методы повышения кпд.
- •48. Воздушные холодильные машины.
- •49. Рабочий процесс двухтактного и четырехтактного двигателя внутреннего сгорания.
- •50. Индикаторные и эффективные характеристики двигателей внутреннего сгорания
- •51. Рабочий процесс и характеристики гту.
14. Процессы изменения состояния идеальных газов.
При
изучении процессов изменения состояния
идеальных газов, наряду с общими
соотношениями по расчету термодинамических
процессов, следует использовать уравнение
Клапейрона
![]() и
закон Джоуля
и
закон Джоуля
![]()
![]() в соответствии с которыми для идеального
газа справедливы следующие выражения:
в соответствии с которыми для идеального
газа справедливы следующие выражения:
если
![]() ,
то
,
то
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Из уравнений (1)(4) следует, что для идеального газа процессы изопотенциальный (pv =idem), изотермический (T = idem), изоэнергетический (u= idem) и изоэнтальпийный (h = idem) тождественны и, следовательно, показатели этих процеcсов равны
![]() .
.
Характеристика расширения или сжатия процессов, в которых рабочим телом является идеальный газ, с учетом уравнения Клапейрона может быть определена по соотношению температур
![]() =
=
![]() .
.
Изменения удельных значений внутренней энергии и энтальпии идеального газа в процессе в соответствии с законом Джоуля находится по следующим формулам:
![]() ;
;
![]() .
.
Показатель адиабатного процесса для идеального газа определяется как соотношение изобарной и изохорной теплоемкостей
k
=
ns
=
![]() =
=
![]() =
=
![]() =
=
![]() .
.
На
основании закона Майера (![]() )
показатель адиабаты для идеального
газа может быть определен из следующего
соотношения:
)
показатель адиабаты для идеального
газа может быть определен из следующего
соотношения:
k
=
![]() =
=![]() >1.
>1.
Для
идеального газа показатель изоэнергетического
процесса
![]() и поэтому удельное количество теплоты
в элементарном процессе может быть
определено по формуле
и поэтому удельное количество теплоты
в элементарном процессе может быть
определено по формуле
![]() .
.
15. Работа и теплообмен в политропных процессах идеальных газов.
Политропным процессом с постоянным показателем называется обратимый термодинамический процесс изменения состояния простого тела, подчиняющийся уравнению, которое может быть представлено в следующих формах:
![]() ;
;
![]() ;
(1.99)
;
(1.99)
![]() =
=
![]() ,
(1.100)
,
(1.100)
где п – показатель политропы, являющий в рассматриваемом процессе постоянной величиной, которая может иметь любые частные значения - положительные и отрицательные (- n +).
Выражения конечных (интегральных) величин термодинамической и потенциальных работ в политропных процессах рассчитываются по следующим соотношениям
![]() .
(1.102)
.
(1.102)
![]() ,
(1.103)
,
(1.103)
где
![]() – характеристика процесса расширения
или сжатия.
– характеристика процесса расширения
или сжатия.
Соотношение
для определения характеристики расширения
или сжатия в рассматриваемом процессе
![]() определяется с учетом зависимостей
(1.101а) и имеет следующий вид:
определяется с учетом зависимостей
(1.101а) и имеет следующий вид:
![]() =
=
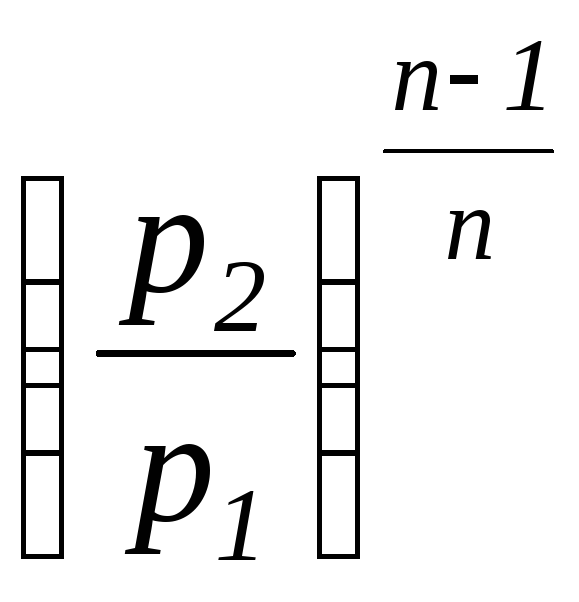 =
=
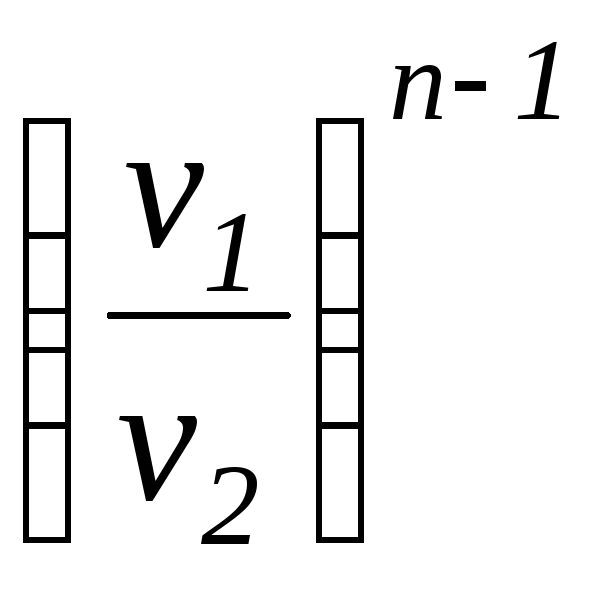 .
(1.104)
.
(1.104)
Расчетное выражения теплообмена для простых тел выводится на основе рассмотрения выражения первого начала термодинамики и имеет следующий вид
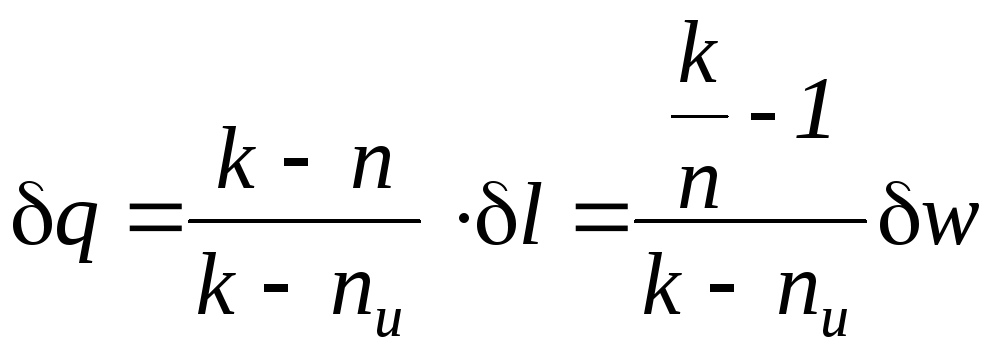 .
(1.105)
.
(1.105)
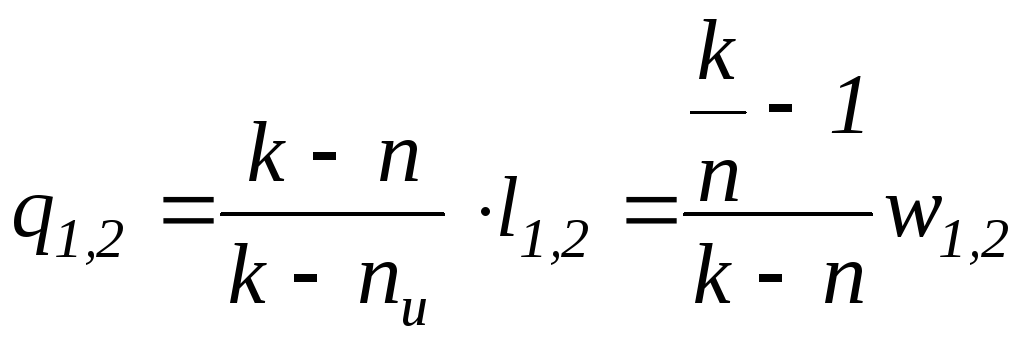 ,
(1.106)
,
(1.106)
где k – показатель адиабаты, n – показатель политропы, nu – показатель изоэнергетического процесса.
Для
конкретных процессов, характеризующихся
неизменным значением какой-либо функции
или параметра состояния (z
= p,v,T,
u,
h,
s),
показатель процесса определяется
соотношением:
![]() .
.
Расчетные зависимости показателей термодинамических процессов получаются с использованием диф. соотношений уравнения состояния простого тела F (р, v, T) = 0:
изотермический
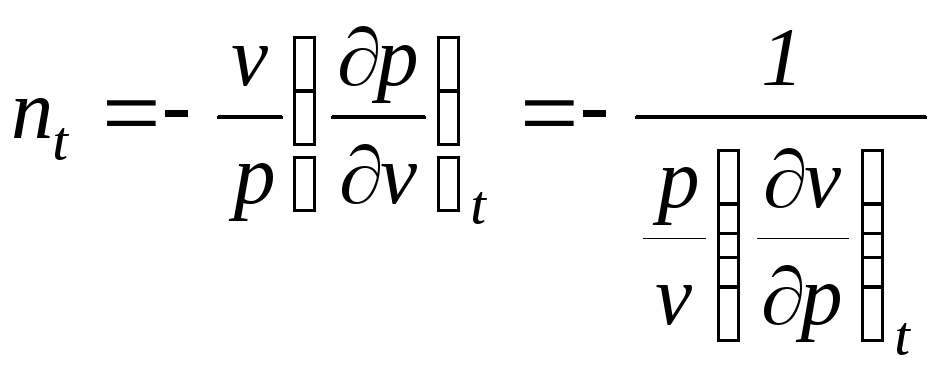 ,
,
адиабатный
![]() ,
,
изоэнергетический
![]() ,
,
изоэнтальпийный
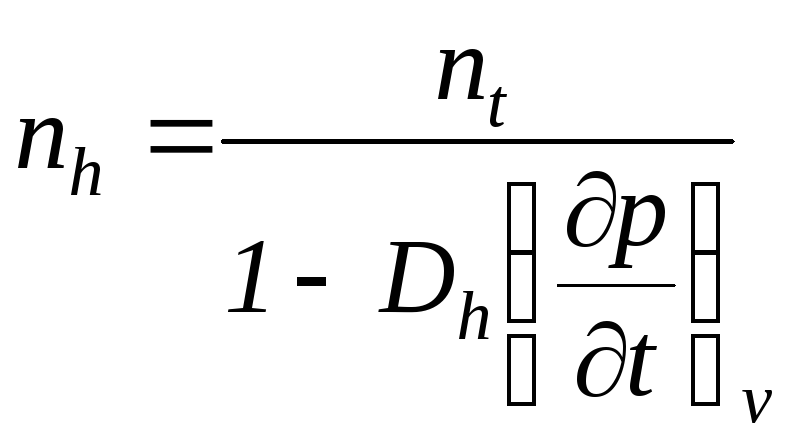
Для
идеального газа процессы изопотенциальный
(pv
=idem),
изотермический (T
= idem),
изоэнергетический (u=
idem)
и изоэнталыпийный (h
= idem)
тождественны и, следовательно, показатели
этих процеcсов
равны:
![]() .
.
Важную
роль в технических расчетах играют
внешнеадиабатические процессы (![]() ).
).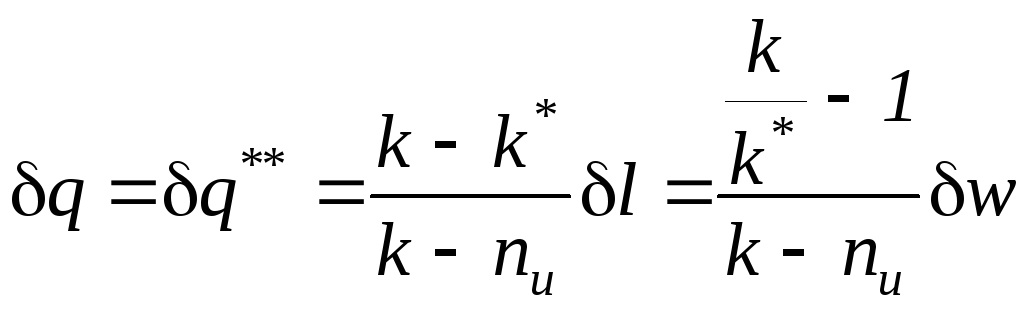
Отсюда
расчетные выражение для определения
показателя внешнеадиабатического
процесса:
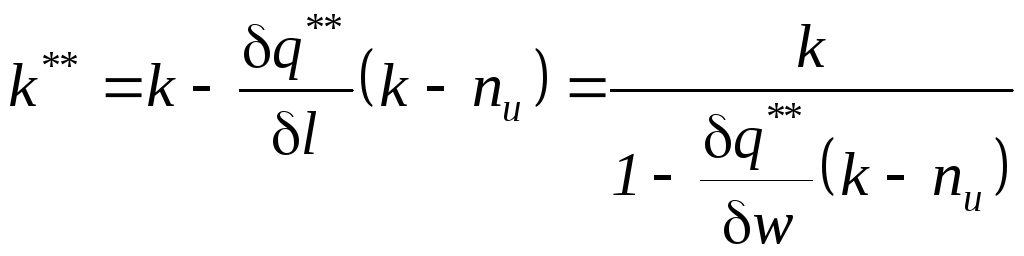
Необратимые
потери имеют всегда положительный знак
![]()
Окончательно
имеем:
![]() .
.
Знаки
![]() перед коэффициентами необратимых потерь
(
перед коэффициентами необратимых потерь
(![]() )
есть знаки соответствующих работ
)
есть знаки соответствующих работ![]() .
.
