2.4.Ранг матрицы. Теорема Кронекера-Капелли.

Пусть дана матрица

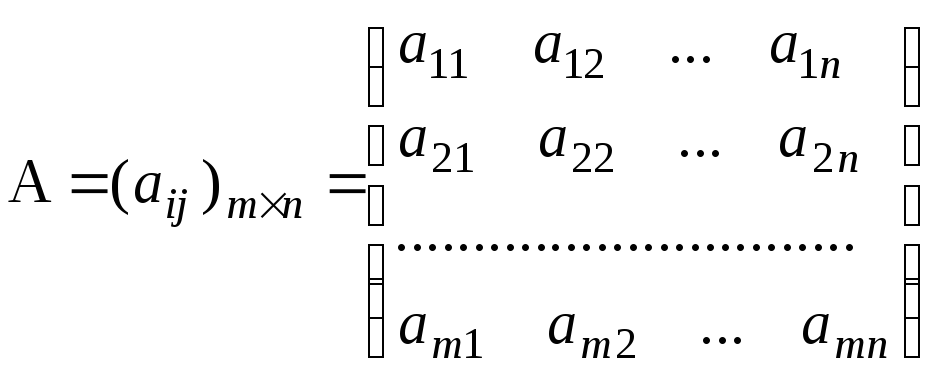
Эту матрицу можно рассматривать как блочную матрицу, т.е. матрицу-столбец вида

А = ,

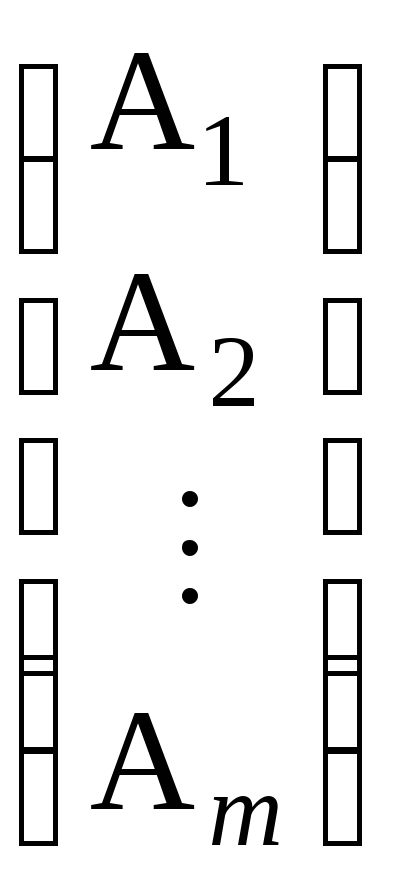элементами которой являются матрицы-строки А_i = (a_i1 a_i2 … a_in) – строки матрицы А. Рассматривая строки матрицы А как векторы линейного пространства Rⁿ, можно говорить об их линейной зависимости и независимости.

Можно показать, что k строк матрицы А линейно независимы тогда и только тогда, когда существует отличный от нуля минор k-го порядка, составленный из элементов этих строк.

Например, в матрице 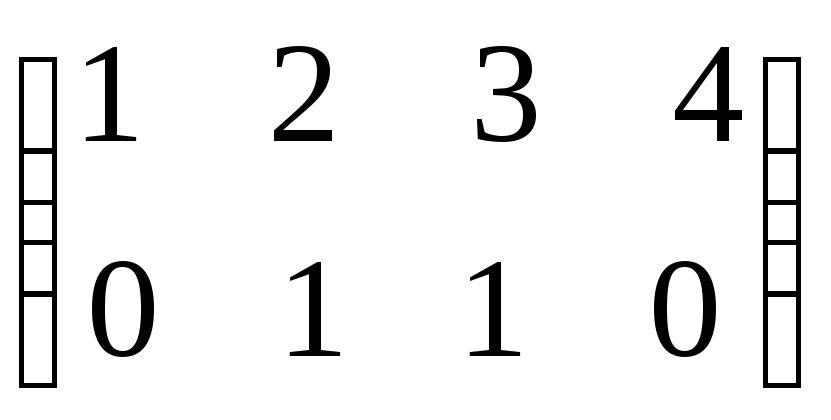строки линейно независимы, т.к. минор= 1 0.

В матрице 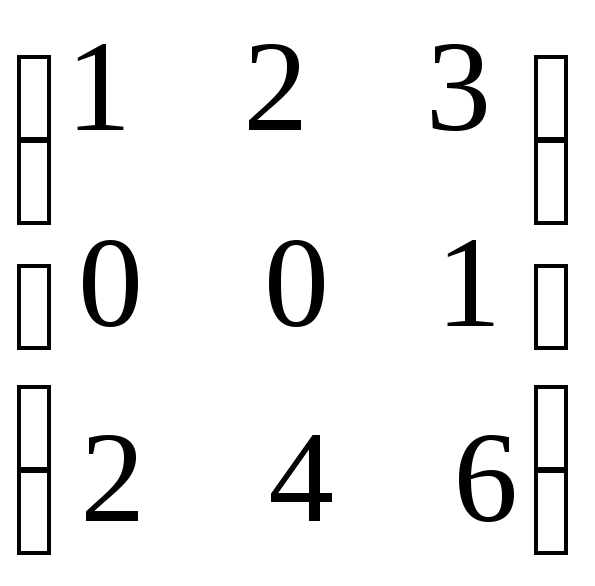линейно независимыми являются первая и вторая строки, или вторая и третья, т.к., например, минор=10, или минор . В то же время, все три строки являются линейно зависимыми, т.к. минор третьего порядка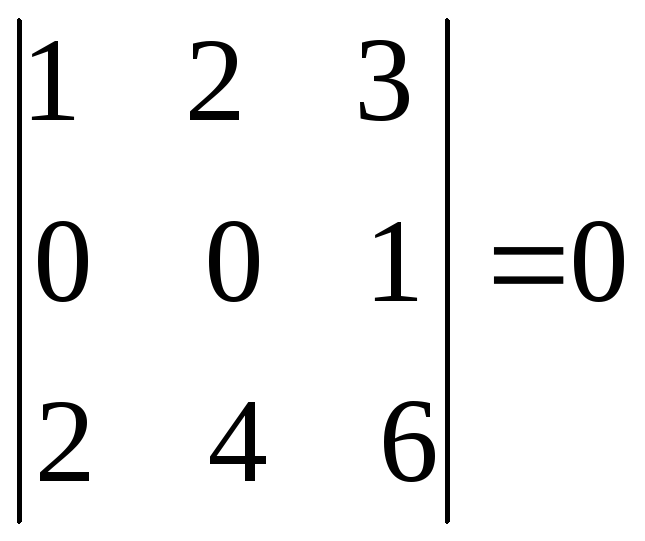(он имеет две пропорциональные строки).

Определение 2.6.

Максимальное число линейно независимых строк матрицы А называют рангом этой матрицы.

Ранг матрицы А обозначается rangA или r(A).

Ранг матрицы обладает свойствами:

• ранг матрицы А равен наивысшему порядку отличных от нуля миноров матрицы;

• для матрицы А = (а_ij)_mn 0 r(A)  min(m, n), причем r(A) = 0 тогда и только тогда, когда А – нулевая матрица;

• для квадратной матрицы А порядка п r(A) = п тогда и только тогда, когда А–невырожденная;

• r(A) =r(A^т);

• ранг матрицы не изменится, если вычеркнуть из нее или приписать к ней нулевой ряд (т.е. строку или столбец, состоящие из одних нулей);

• ранг матрицы А_Э, полученной из матрицы А с помощью элементарных преобразований, равен рангу исходной матрицы А.

Можно использовать следующий алгоритм вычисления ранга матрицы:

1) Заданную матрицу А элементарными преобразованиями привести к треугольной или трапециевидной форме А_Э.

2) Записать r(A) = r(А_Э) = k , т.е. числу ненулевых строк матрицы А_Э, так как минор k -го порядка

,

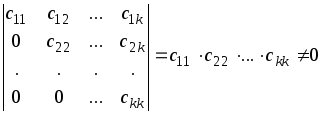а все миноры более высоких порядков равны нулю, поскольку содержат нулевые строки.

Понятие ранга матрицы может быть использовано для исследования СЛУ.

Теорема 2.3(Кронекера-Капелли)

Система линейных уравнений совместна тогда и только тогда, когда ранг r(A) основной матрицы системы равен рангу r() расширенной матрицы, т.е. .

Число r = называют рангом системы уравнений.

Исследование системы с помощью ранга можно проводить следующим образом:

1. Вычислить r(A) и r(); если r(A)  r(), то система несовместна;

2. Если r(A) = r(А) = r , то система совместна и

а) при r = п имеет единственное решение;

б) при r < n имеет бесчисленное множество решений. В этом случае r неизвестных СЛУ являются базисными, остальные п – r неизвестных – свободными. Базисными неизвестными выбираются те, коэффициенты при которых в матрице А_Э образуют отличный от нуля минор (базисный минор).

Рассмотрим пример.

Исследовать СЛУ и в случае совместности – решить.

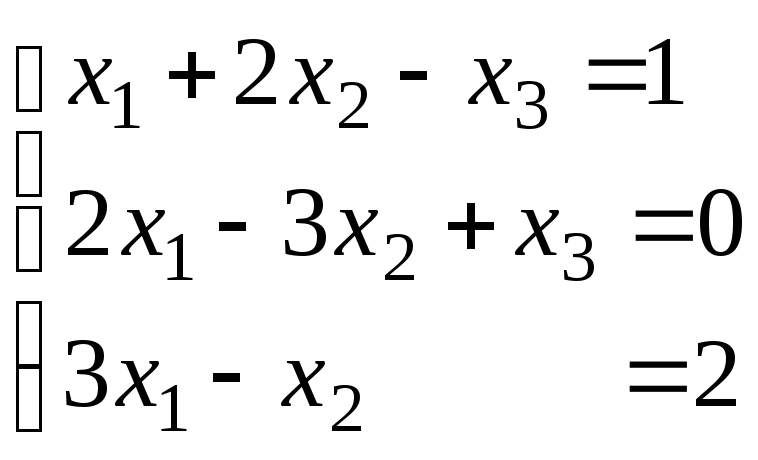
Запишем расширенную матрицу системы и найдем ее ранг, преобразовав к трапециевидной форме

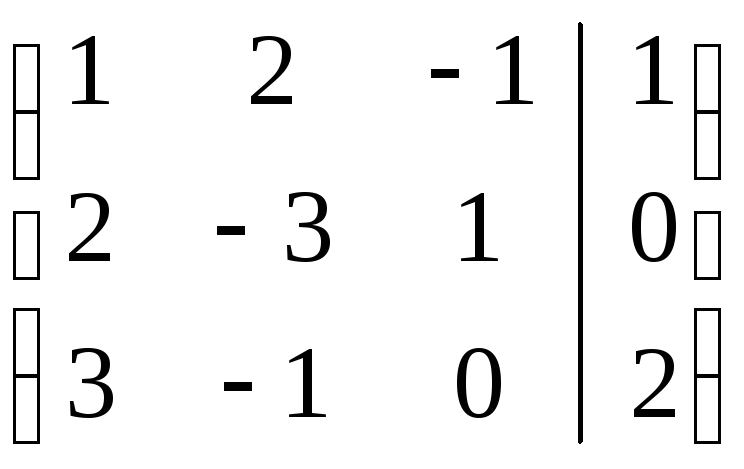
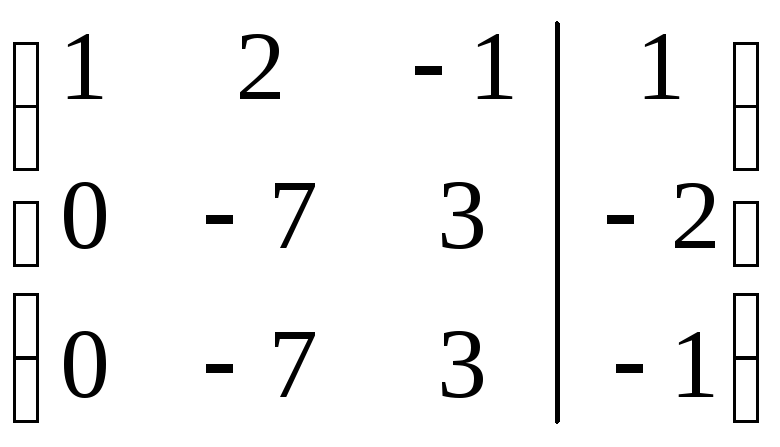
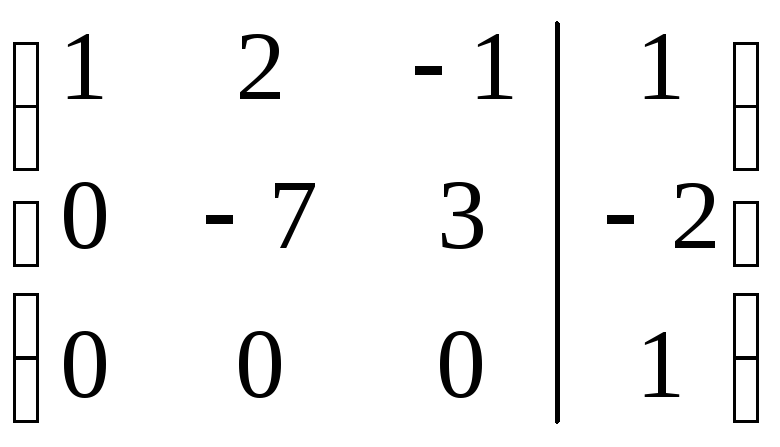А= = =А_Э.

Ранг матрицы А_Э равен 3 (три ненулевые строки), а значит и r = 3. Однако матрица, элементы которой стоят слева от вертикальной черты – есть матрица А_Э для основной матрицы системы (которая записана в А слева от вертикальной черты). А эта матрица имеет только две ненулевые строки, что означает r(А_Э) = r(А) = 2. Таким образом , r(A)  r и в этом случае система несовместна.

Если же рассмотреть систему 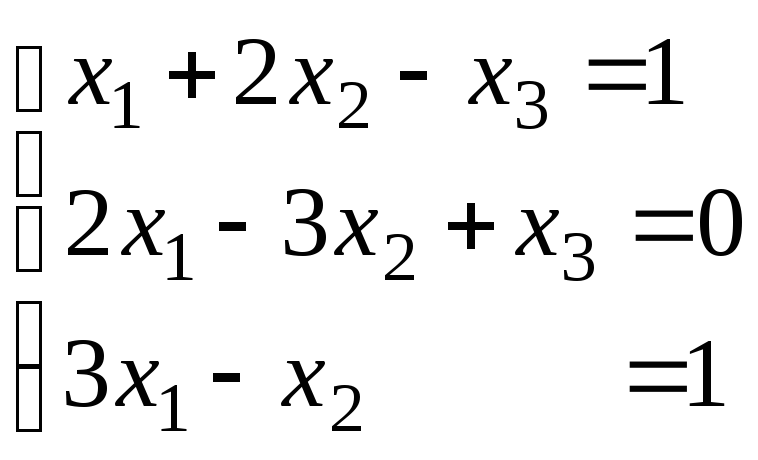, то нетрудно убедиться в ее совместности:

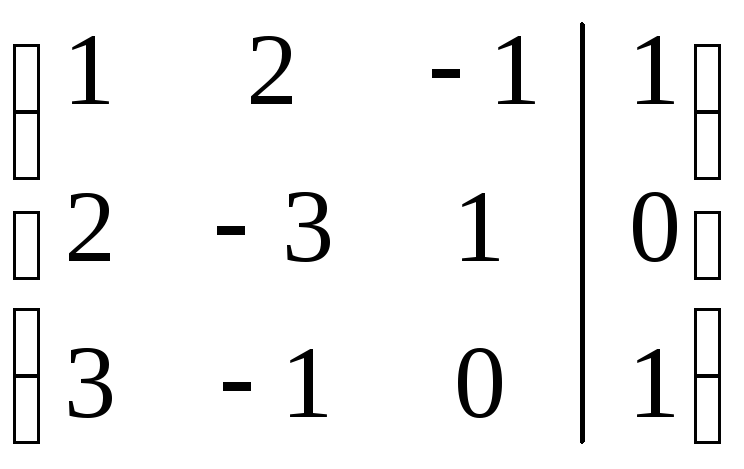
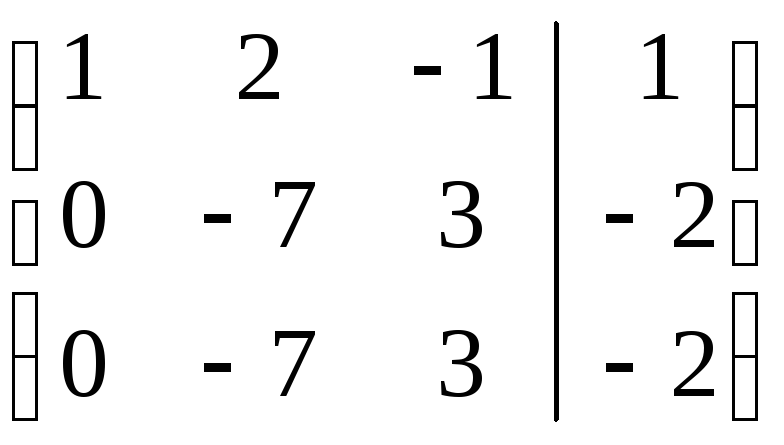
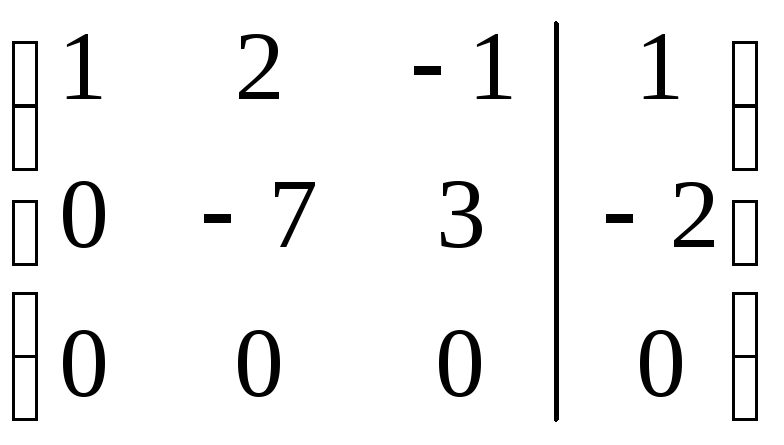А= = =А_Э,

значит, r(A) = r = r = 2 – система совместна. Число неизвестных п = 3 и r < n, в этом случае система имеет множество решений.