69

Тема 4. Аналитическая геометрия

4.1. Предмет аналитической геометрии

Аналитическая геометрия – это раздел геометрии, в котором для исследования геометрических объектов (точек, прямых, плоскостей, линий, поверхностей, тел) используются средства алгебры и математического анализа.

В основе аналитической геометрии лежит метод координат. Суть его в следующем: на плоскости или в пространстве фиксируется вспомогательный геометрический объект – система координат, которая позволяет каждой точке плоскости или пространства ставить в соответствие систему чисел, называемых координатами точки, а всякий геометрический объект рассматривается, как совокупность точек, обладающий общим (характеризующим) свойством. Это свойство с помощью координат точек можно описать в виде уравнения, неравенства, системы уравнений или неравенств (а, значит, с помощью функций). Тогда изучение объекта можно свести к изучению этих уравнений, неравенств.

Основными задачами аналитической геометрии являются следующие:

1. Используя характеризующее свойство точек объекта, описать его с помощью уравнения, неравенства.

2. Зная алгебраический образ геометрического объекта (его уравнение, неравенство,…) изучить свойства этого объекта.

В дальнейшем мы будем предполагать, что на плоскости или в пространстве задана ПДСК. Тогда каждой точке плоскости (пространства) соответствует пара чисел (х, у) (тройка чисел (х, у, z)) и наоборот, каждой совокупности чисел соответствует точка. Так как пара (х, у) есть строка длины два, а тройка (х, у, z) есть строка длины три, то множество точек плоскости и пространства можно идентифицировать с пространствами R² и R³ соответственно. Поэтому в дальнейшем множество точек плоскости будем обозначать R², а множество пространственных точек – R³.

Определение 4.1.

Уравнением линии на плоскости (в R²) называется такое уравнение с двумя переменными, которому удовлетворяют координаты всех точек заданной линии и только они.

В общем виде уравнение линии на плоскости записывают так

F(x,y) = 0.

Если F₁(x, y) = 0 –уравнение одной линии, а F₂(x, y) = 0 –уравнение другой, то точки пересечения этих линий находят из системы

.

Уравнение линии может быть задано в виде у = f(x) или 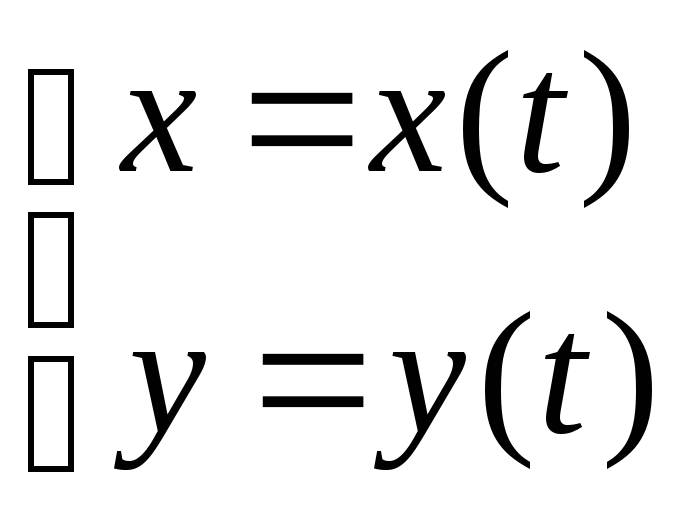(параметрическое задание линии).

С точки зрения математического анализа, уравнение линии – это задание функции (явное или неявное), причем однозначность функции в этом случае не оговаривается.

Чтобы составить уравнение линии, нужно

1. взять произвольную точку М(х, у) этой линии (ее называют текущей точкой);

2. записать характеризующее свойство точек линии в виде символьного равенства;

3. входящие в это равенство отрезки выразить через координаты точки М(х, у) и других известных из условия задачи точек;

4. упростить полученное уравнение.

Пример: Составить уравнение и построить линию, каждая точка которой равноудалена от точки А(2, 0) и от прямой у – 2 = 0.

Решение:

Сделаем схематичный чертеж (рис.1). Пусть точка М(х, у) – текущая точка искомой кривой. Тогда, по условию,

|AM| = |PM|,

где РМ – перпендикуляр, опущенный из точки М на прямую у – 2 = 0.

Запишем это равенство через координаты точек А, М, Р. Имеем

|AM| = .

. Из чертежа легко определяем координаты точки Р (х, 2), тогда

|PM| = .

Получим– это и есть искомое уравнение линии. Преобразуем его.

,

х² – 4х + 4 + у² = у² – 4у + 4,

х² – 4х = –4у,

,

,

у = 1 – 0,25(х –2)² – уравнение параболы (рис.2).

Определение 4.2.

Уравнением поверхности в пространстве (в R³) называется такое уравнение с тремя переменными, которому удовлетворяют координаты всех точек поверхности и только они.

Уравнение поверхности записывают в виде F(x, y, z) = 0.

Линию в пространстве R³ можно рассматривать как пересечение двух поверхностей, поэтому в R³ линия определяется системой уравнений этих поверхностей:

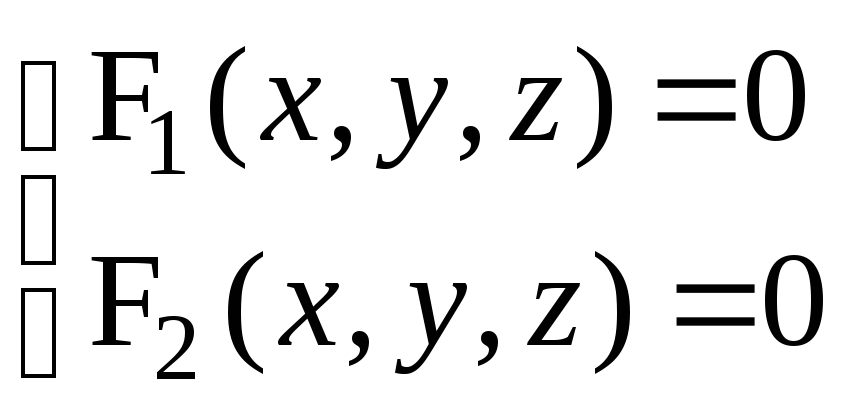
Линию в пространстве можно также задать параметрическими уравнениями

,

каждое уравнение этой системы определяет закон изменения соответствующей координаты текущей точки линии в зависимости от изменения некоторого параметра t. Такими уравнениями может быть задана траектория движения материальной точки.