17

Тема 1. Матрицы. Определители

1.1.Определение и виды матриц

Многие математические модели содержат наборы однотипных величин, причем эти наборы обнаруживают определенные закономерности, проявляющие себя независимо от природы величин и от того, какой раздел математики был задействован в составлении модели, приведшей к рассмотрению этого набора величин. Для изучения таких закономерностей в математике существует специальный аппарат – матричное исчисление.

Определение 1.1.

Матрицей размерности тп (читается т на п) называется прямоугольная таблица вида

,

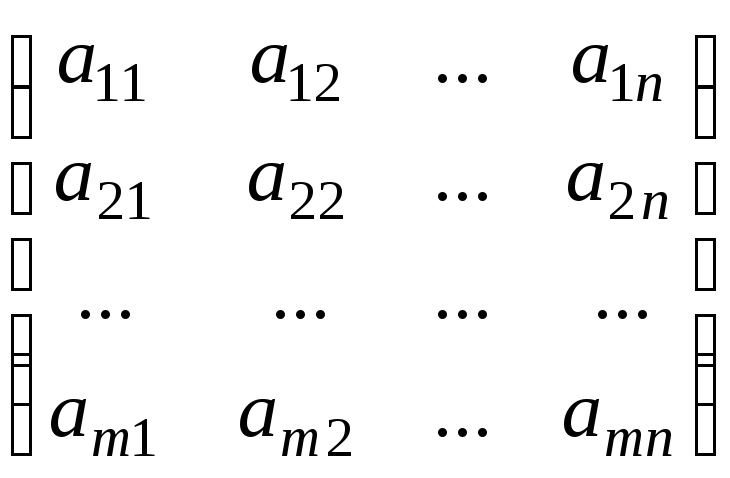образованная их элементов некоторого множества и содержащая т строк и п столбцов.

Элементы а_ij рассмотренного множества, из которых состоит матрица, называются элементами матрицы.

Матрицы обозначаются заглавными латинскими буквами: А, В, С, …, а их элементы – соответствующими прописными, например а_ij. При этом первый индекс элемента определяет номер строки, а второй – номер столбца, в котором этот элемент стоит. Сокращенно матрицу А размерности тп с элементами а_ij записывают так:

А = (а_ij)_тп.

Матрица размерности т1 (т.е. матрица, имеющая один столбец), называется матрицей-столбцом:

.

Матрица размерности 1п (т.е. матрица, имеющая только одну строку) называется матрицей-строкой:

А_1п = (а₁₁ а₁₂ … а_1п).

Если т = п , т.е. число строк матрицы совпадает с числом столбцов, то матрица называется квадратной: А = (а_ij)_пп. При этом число п называется порядком квадратной матрицы.

Элементы а₁₁ , а₂₂ , … , а_пп квадратной матрицы называются элементами главной диагонали матрицы (или просто главной диагональю).

В дальнейшем мы будем рассматривать, в основном, числовые матрицы.

Если все элементы матрицы А = (а_ij)_тп равны нулю, то эта матрица называется нулевой.

Квадратная матрица, все элементы которой, кроме элементов главной диагонали, равны нулю, называется диагональной:

, а_ii  0.

Если в диагональной матрице а₁₁= а₂₂ = … = а_пп = d  0, то матрица называется скалярной. Скалярная матрица, элементы главной диагонали которой равны 1, называется единичной, обозначают единичную матрицу буквой Е:

Е = .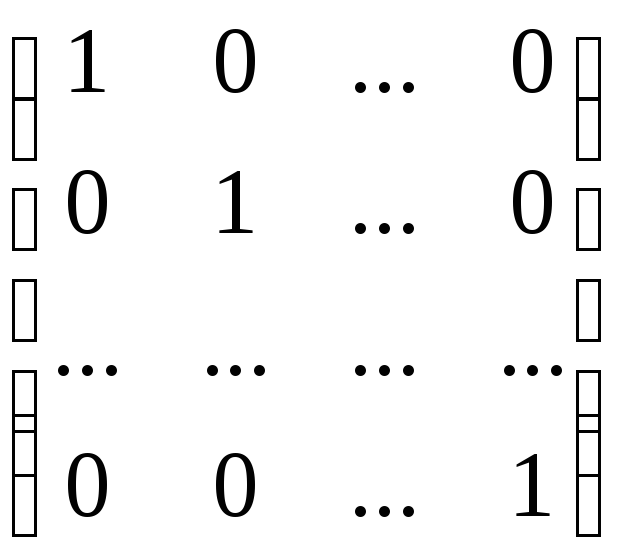

Если в матрице А = (а_ij)_т´п с комплексными элементами заменить все элементы а_ii на их комплексно сопряженные, то полученная матрица А* называется сопряженной к А: А* = (а_ij )_т´п.

1.2.Операции над матрицами

Рассмотрим операции над матрицами.

1. Матрица А^т, получающаяся из матрицы А = (а_ij)_т´п заменой ее строк столбцами, называется транспонированной к А.

А =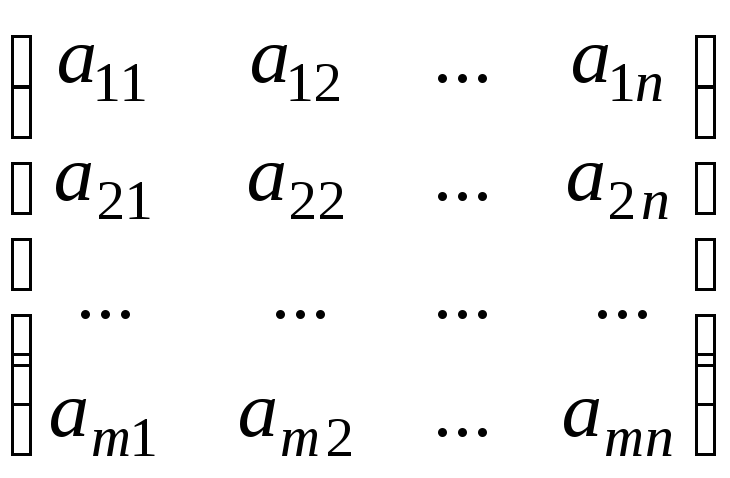 А^т =.

2. Матрицы А = (а_ij)_т´п и В = (b_ij)_т´п одинаковой размерности равны тогда и только тогда, когда равны их соответствующие элементы (т.е. элементы, стоящие на одинаковых местах):

А = В  а_ij = b_ij , i = 1, 2, …, n, j = 1, 2, …, m.

3. Суммой матриц А = (а_ij)_т´п и В = (b_ij)_т´п одинаковой размерности называется матрица С = (с_ij)_т´п, элементы которой равны суммам соответствующих элементов матриц А и В: с_ij = а_ij + b_ij.

4. Произведением матрицы А = (а_ij)_т´п на число  называется матрица А, элементы которой равны произведениям элементов матрицы А на число :

А = (а_ij)_т´п

Операции сложения и умножения на число обладают свойствами:

1. А + В = В + А,

2. А + (В + С) = (А + В) + С,

3. (А + В) = А + В,

4. ( + )А = А + А,

5. (А) = (^.)А.

Доказательство этих свойств легко провести, пользуясь непосредственно определением соответствующих операций.

5. Разность матриц А и В определяется равенством А – В = А + (–1)В.

6. Произведение матрицы А = (а_ij) на матрицу В = (b_ij) есть матрица С, элементы которой находят по правилу

с_ij = a_i1b_1j + a_i2b_2j +... + a_inb_nj,

i = 1,2,...,n, j = 1,2,...,k , т.е. чтобы найти элемент матрицы С, стоящий в i – ой строке и j-ом столбце, нужно взять i- ю строку матрицы А и j-й столбец матрицы В, попарно перемножить их соответствующие элементы и полученные произведения сложить.

Произведение С = АВ матриц А и В определено тогда и только тогда, когда размерности этих матриц удовлетворяют условию

А_т´п ^.В _п´k = С _т´k.

Свойства умножения матриц:

1. (АВ)С = А(ВС),

2. (А + В)С = АС + ВС, А(В + С) = АВ + АС,

3. l(АВ) = (lА)В = А(lВ),

4. (АВ)^т = В^тА^т,

5. АЕ =А, ЕА = А,

6. (АВ)* = B*A*

Доказать эти свойства самостоятельно.

Обратите внимание, умножение матриц не обладает свойством коммутативности: АВ  ВА. Более того, если одно из этих произведений существует, то второе – совсем не обязательно. Например, если А_23 и В_33, то АВ можно найти, а ВА не определено.

Если же выполняется условие АВ = ВА, то матрицы А и В называются перестановочными.

Естественно определить натуральную степень квадратной матрицы по правилу: А^п = . Тогда можно рассматривать и матричный многочлен вида Р(А) =а_пА^п + а_п–1А^п–1 + … + а₁А + а₀Е.

Квадратную матрицу А , удовлетворяющую условию А = А^т, называют симметрической. Для такой матрицы а_ij = a_ji , i, j = 1,2,...,n, i  j.

Квадратную матрицу А, удовлетворяющую условию А = –А^т. называют кососимметрической. Для такой матрицы а_ij = – a_ji при i ¹ j и а_ii = 0, i , j = 1,2,...,n.

Матрица А, удовлетворяющая условию А = A*, называется эрмитовой. Если А* = –A, то матрица А – косоэрмитова матрица.

Матрица А^–1 называется обратной для квадратной матрицы А, если

А^–1А = АА^–1 = Е.

Матрица А, удовлетворяющая условию А^т = А^–1, называется ортогональной матрицей.