
- •Тема 1. Матрицы. Определители
- •1.1.Определение и виды матриц
- •1.2.Операции над матрицами
- •1.3. Определители, их свойства
- •1.4.Обратная матрица
- •Тема 2 . Системы линейных уравнений (слу)
- •2.1.Основные определения и понятия
- •2.2.Решение «квадратных» слу
- •2.3. Решение произвольных слу
- •2.4.Ранг матрицы. Теорема Кронекера-Капелли.
1.3. Определители, их свойства
Каждой квадратной матрице с элементами из числового поля можно поставить в соответствие обобщенную числовую характеристику – определитель.
Определение 1.2.
Определителем второго порядка называется число
![]() .
.
Определителем третьего порядка называется число
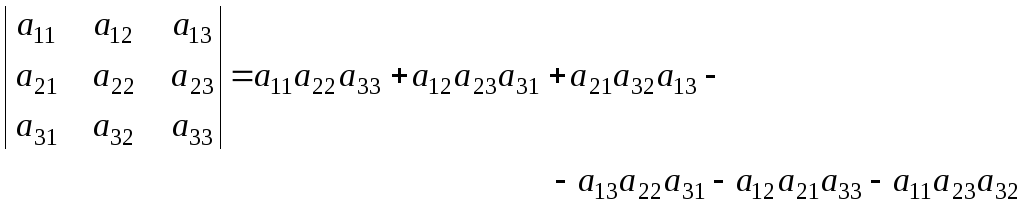
Таким
образом, матрице А =
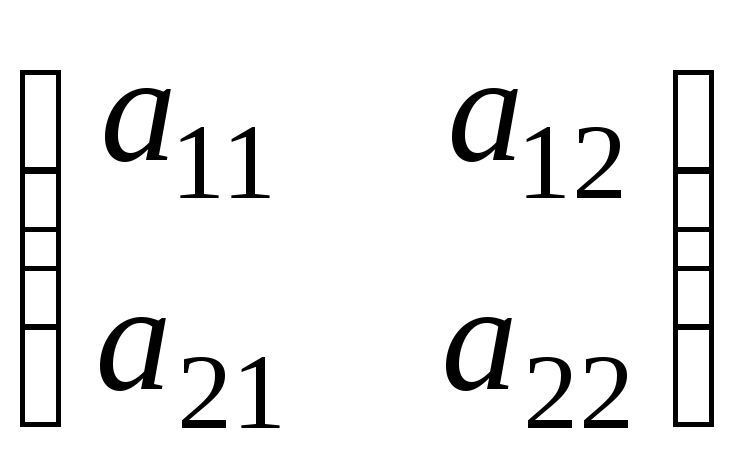 второго порядка ставится в соответствие
число |A| =
второго порядка ставится в соответствие
число |A| =  ,
которое является определителем этой
матрицы. Аналогично, для матрицы третьего
порядка А =
,
которое является определителем этой
матрицы. Аналогично, для матрицы третьего
порядка А = 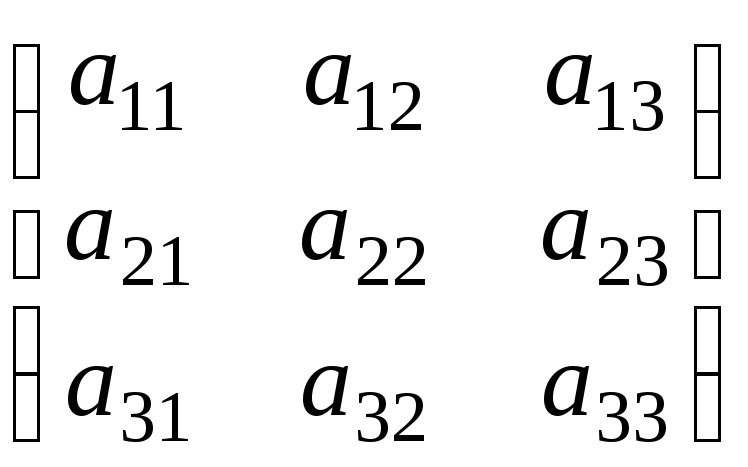 рассматривается ее определитель |A|
=
рассматривается ее определитель |A|
= 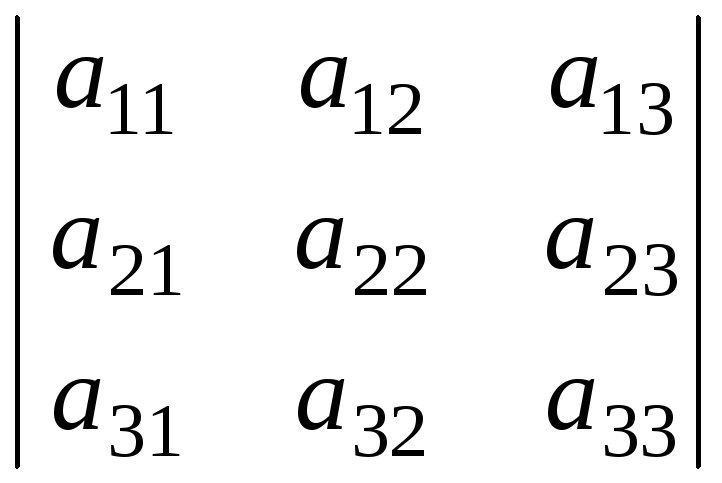 .
Наряду с обозначение |A|
используется обозначение detA.
.
Наряду с обозначение |A|
используется обозначение detA.
Для матрицы А = (а11) первого порядка определителем является, очевидно, само число а11: |A| = а11.
Если вычисление определителя первого и второго порядка не составляет труда непосредственно с помощью определения, то определитель третьего порядка вычислять по определению затруднительно. Поэтому используют различные методы вычисления. Рассмотрим их.
«правило треугольника», которое можно описать с помощью следующей схемы:
S1
S2
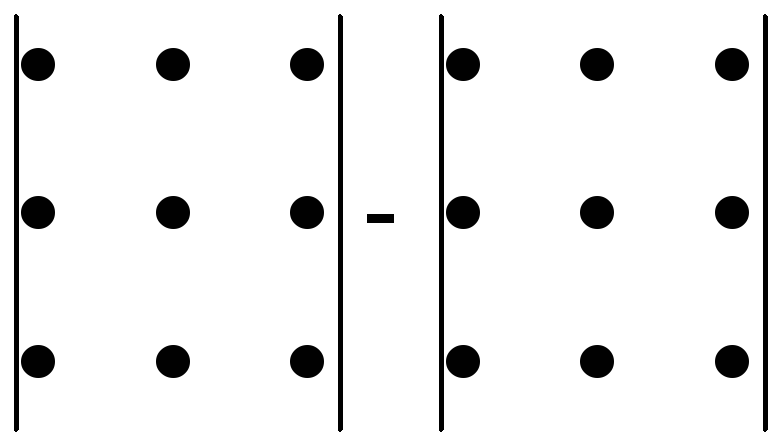
Рисунок 1- Правило треугольника
Согласно этой схеме, от суммы S1 произведений соединенных между собой по три элементов фигуры 1 нужно отнять сумму S2 произведений соединенных элементов фигуры 2.
2) правило Саррюса, суть которого в следующем:
справа от определителя выписать первый и второй столбцы этого определителя;
затем от суммы S1 произведений элементов, стоящих на главной диагонали и параллельных ей направлениях, отнять сумму S2 произведений элементов, стоящих на побочной диагонали (идущей из правого верхнего угла в левый нижний) и ее параллелях:
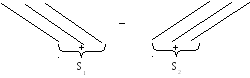
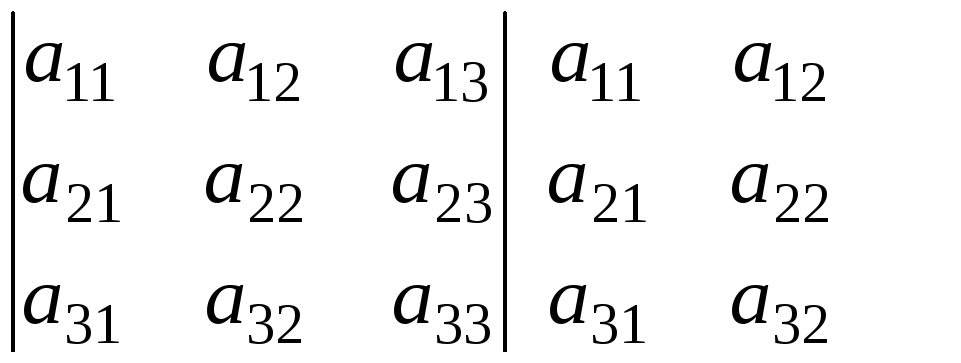
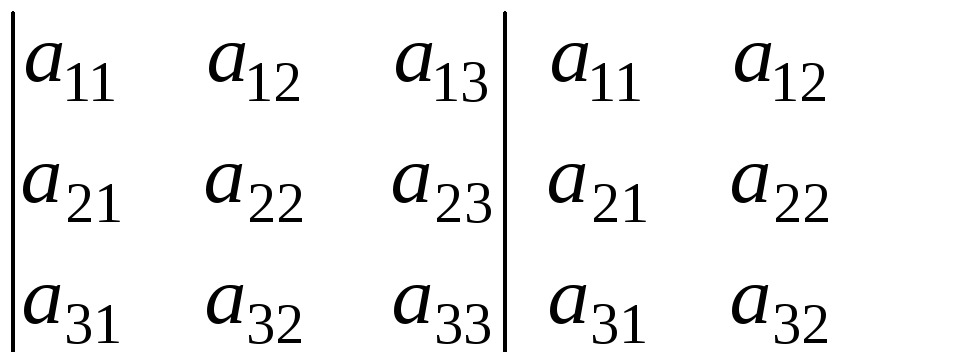 ,
,
Еще раз подчеркнем, что эти способы вычисления применимы только для определителя третьего порядка.
Рассмотрим пример. Вычислим определитель, используя правило треугольника
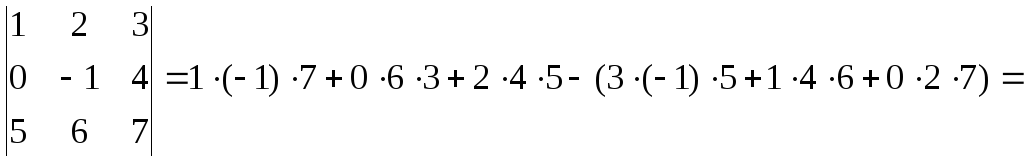
![]() .
.
Вычислим тот же определитель по правилу Саррюса

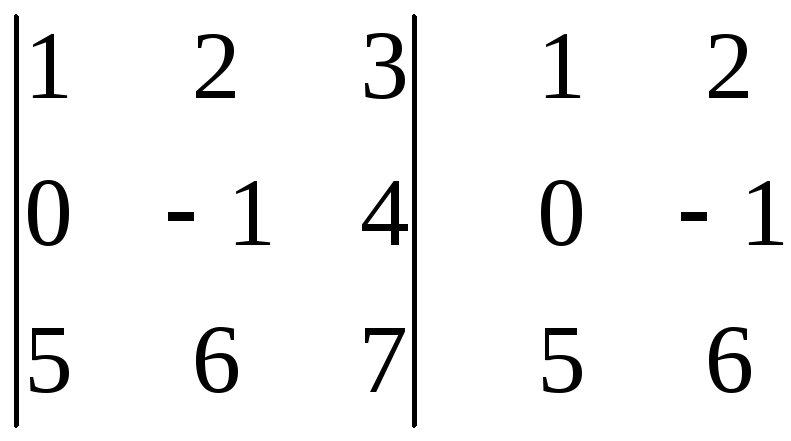 =
(1.(–1).7
+2.4.5
+ 3.0.6)
– (5.(–1).3
+6.4.1
+7.0.2)
=
=
(1.(–1).7
+2.4.5
+ 3.0.6)
– (5.(–1).3
+6.4.1
+7.0.2)
=
= (–7 + 40 + 0) – (–15 + 24 + 0) = 33 – 9 = 24.
Заметьте, что получили не только точно такой же результат, что и по правилу треугольника, но и оперировали такими же суммами произведений элементов определителя, что и по правилу треугольника, разве что записанными в другом порядке.
Понятие определителя п-го порядка введем индуктивно, считая введенным понятие определителя (п–1) –го порядка.
Определение 1.3.
Алгебраическим дополнением элемента аij квадратной матрицы А = (аij) называется умноженный на (–1)i+j определитель, составленный из элементов матрицы А, оставшихся после вычеркивания i-й строки и j-го столбца матрицы. Обозначается алгебраическое дополнение Аij.
Например,
для матрицы А =
![]() имеем:А11
= 5, А12
= –4, а для матрицы А
=
имеем:А11
= 5, А12
= –4, а для матрицы А
= 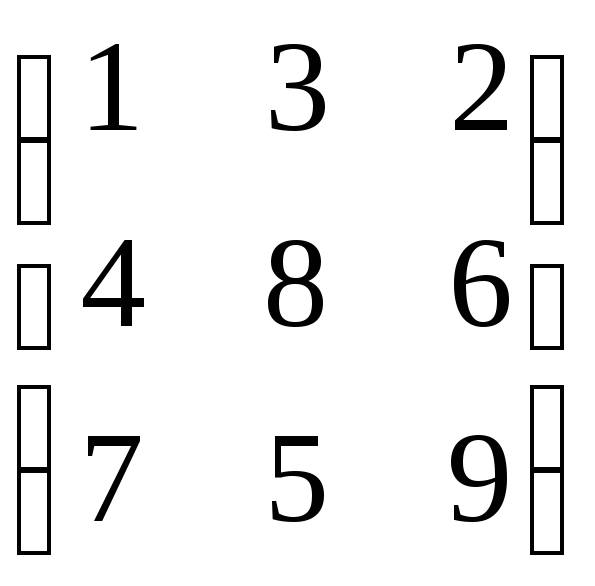 получим, например, А23
= –
получим, например, А23
= –
![]() ,
илиА31
=
,
илиА31
=
![]() .
.
Определение 1.4.
Определителем п – го порядка называется число
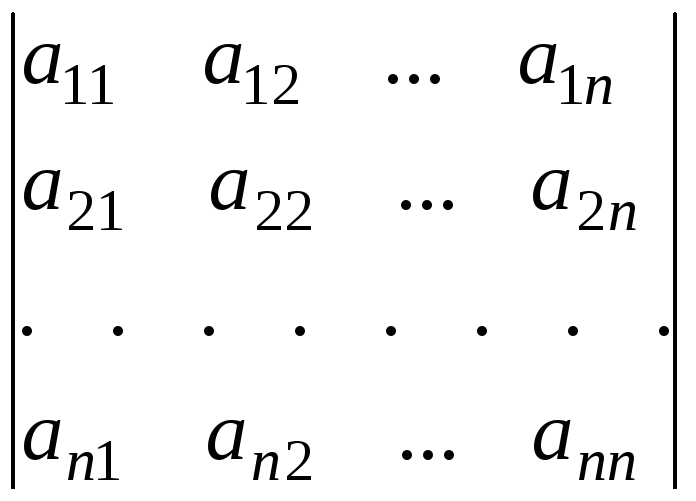 =
а11.А11
+ а12.А12
+ ... + а1п.А1п,
(*)
=
а11.А11
+ а12.А12
+ ... + а1п.А1п,
(*)
где А1j (j = 1, 2, …, n) – алгебраические дополнения элементов первой строки определителя.
Правую часть равенства (*) называют разложением определителя по первой строке.
Таким образом, для матрицы А порядка п определитель равен
|A|
=
![]() .
.
Например,
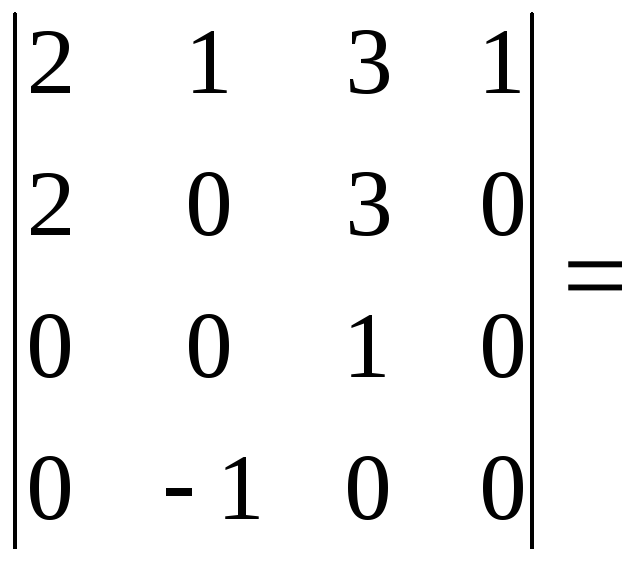
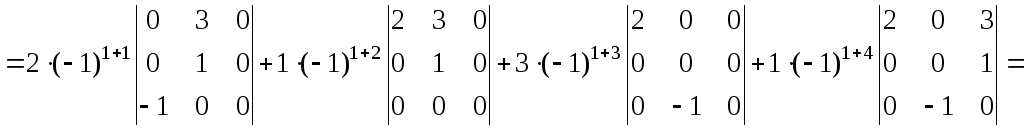
![]()
Свойства определителей:
|Aт| = |A|.
Определитель изменит знак, если поменять местами любые две строки или любые два его столбца.
Определитель равен нулю, если он имеет две пропорциональные строки, или два пропорциональных столбца. В частности, если две строки или два столбца определителя равны, то этот определитель равен 0.
Общий множитель элементов строки (или столбца) можно выносить за знак определителя. В частности, если все элементы строки (или столбца) равны нулю, то и определитель равен нулю.
Если каждый элемент строки (столбца) определителя равен сумме двух слагаемых, то определитель равен сумме двух определителей, в одном из которых указанная строка (столбец) состоит из первых слагаемых, а в другом – из вторых. Остальные строки этих определителей те же, что и в исходном определителе:
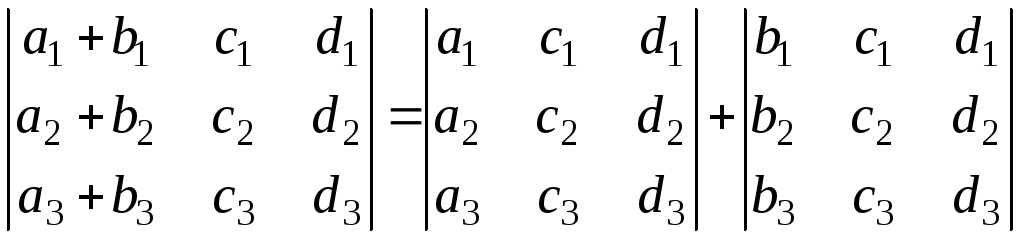
Определитель не изменится, если к элементам какой-либо строки (столбца) прибавить элементы другой строки (столбца), умноженные на произвольный множитель.
Определитель равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения: |A| =
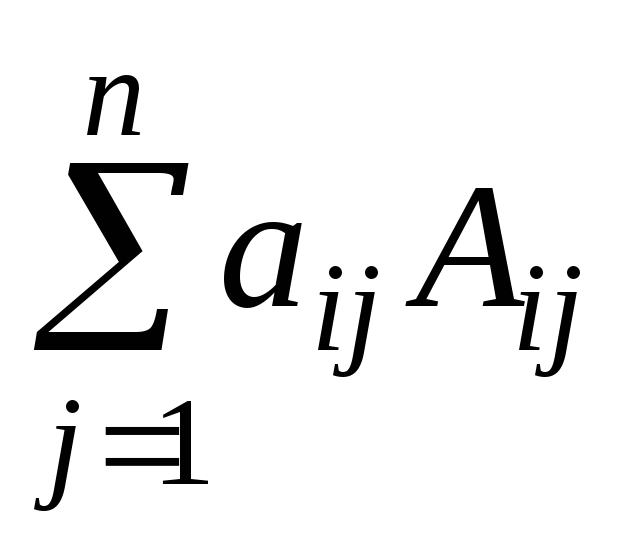 ,
(i =
1, 2, …, п).
Сумма
произведений элементов строки (столбца)
определителя на алгебраические
дополнения к элементам другой строки
(другого столбца) равна нулю:
,
(i =
1, 2, …, п).
Сумма
произведений элементов строки (столбца)
определителя на алгебраические
дополнения к элементам другой строки
(другого столбца) равна нулю:
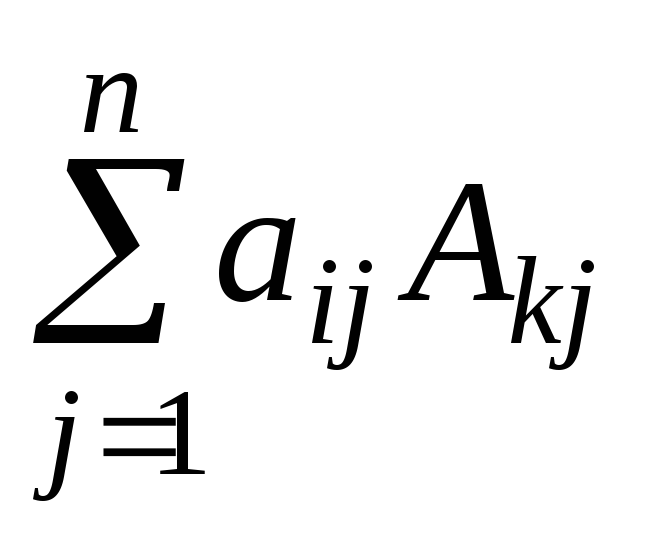 =
0,k
j.
=
0,k
j.Определитель треугольной матрицы (у которой под главной диагональю или над ней стоят все 0) равен произведению диагональных элементов:
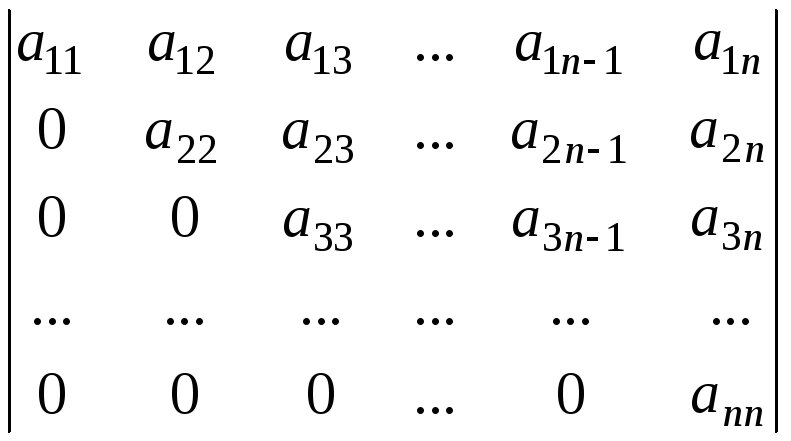 = а11.
а22.
а33.
….
апп.
Такой
определитель называют определителем
треугольного вида.
= а11.
а22.
а33.
….
апп.
Такой
определитель называют определителем
треугольного вида.
Учитывая свойство 7, определитель можно вычислять, не только разлагая его по первой строке, но и по любой другой строке или столбцу.
Например, в рассмотренном выше определителе вычисление удобнее проводить, разлагая по четвертому столбцу или, по третьей или четвертой строке:
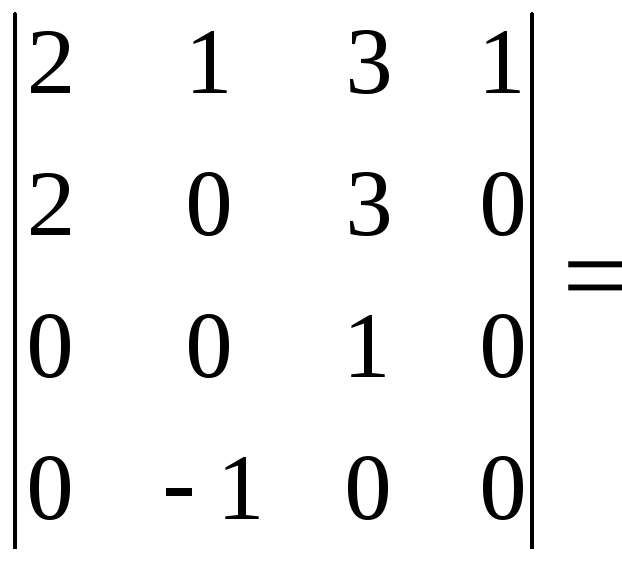
 .
.
Используя свойство 6, определитель можно преобразовать к треугольному виду, а затем вычислить, используя свойство 8.
Отметим еще несколько свойств определителей:
|AB| = |A|.|B|
|E| = 1
|A| =n|A|, Ann
|A + B| |A| + |B|.
Докажите эти свойства!
Матрица, определитель которой отличен от нуля, называется невырожденной. Если |A| = 0, то матрица А – вырожденная.
Дадим еще одно определение, необходимое нам в дальнейшем
Определение 1.5.
Всякий определитель, составленный из элементов заданной матрицы А, стоящих на пересечении k строк и k столбцов (k min(m, n)), называется минором k-го порядка матрицы А.
Например,
для матрицы А =
 минорами второго порядка, например,
являются определители:
минорами второго порядка, например,
являются определители:![]() ,
,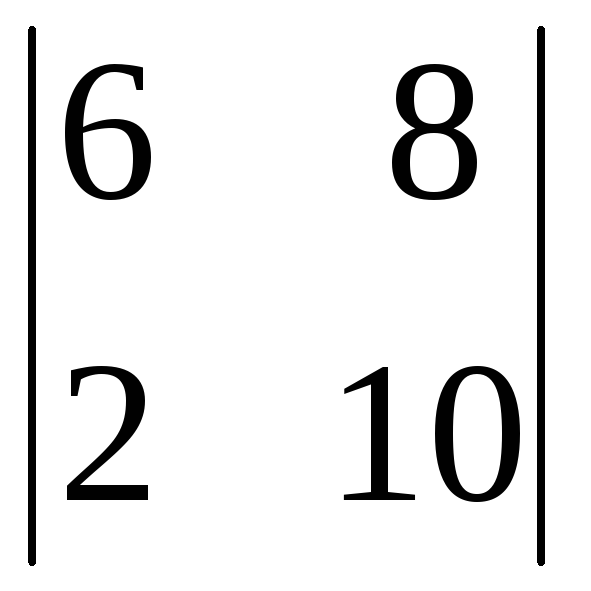 ,
а один из миноров третьего порядка имеет
вид
,
а один из миноров третьего порядка имеет
вид
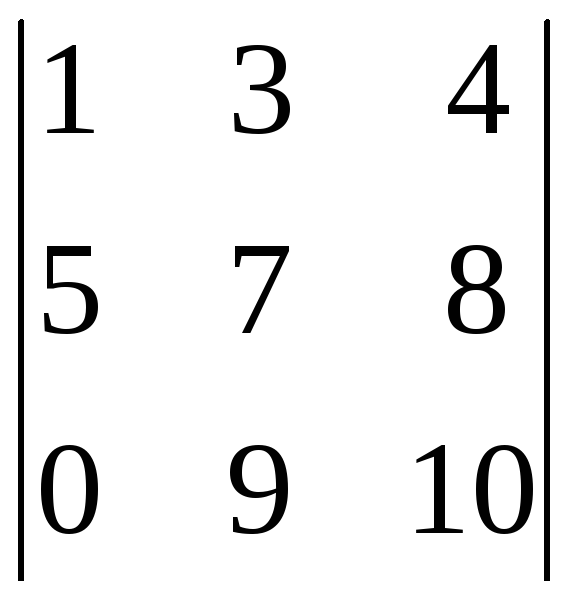 .
.
Понятие определителя можно ввести и для матриц с элементами из любого поля. Тогда определитель есть также элемент этого поля. «Вычисление» такого определителя также можно проводить описанными выше приемами.
