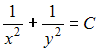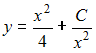Документ Microsoft Office Word
.docx
Решение:
Так
как коэффициенты данного ряда Тейлора
вычисляются по формуле
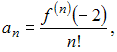то
вычислим последовательно
производные:
Тогда
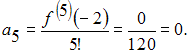
ЗАДАНИЕ N 9
отправить
сообщение разработчикам
Тема:
Типы дифференциальных уравнений
Начало формы
Конец формы
Уравнение
является …
|
|
|
|
линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами |
|
|
|
|
линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами |
|
|
|
|
дифференциальным уравнением второго порядка, допускающим понижение порядка |
|
|
|
|
уравнением Бернулли |
Решение:
Уравнение
можно
представить в виде
где
Следовательно,
данное уравнение является линейным
неоднородным дифференциальным уравнением
второго порядка с постоянными
коэффициентами.
ЗАДАНИЕ N 10
отправить
сообщение разработчикам
Тема:
Дифференциальные уравнения с разделяющимися
переменными
Начало формы
Конец формы
Общее
решение дифференциального уравнения
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Разделим
переменные в исходном уравнении:
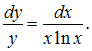Интегрируем
обе части последнего равенства
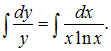Вычисляя
интегралы, получаем
или
где
ЗАДАНИЕ
N 11
отправить
сообщение разработчикам
Тема:
Линейные неоднородные дифференциальные
уравнения первого порядка
Начало формы
Конец формы
Общее
решение дифференциального уравнения
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ
N 12
отправить
сообщение разработчикам
Тема:
Линейные дифференциальные уравнения
второго порядка с постоянными
коэффициентами
Начало формы
Конец формы
Общий
вид частного решения
линейного
неоднородного дифференциального
уравнения второго порядка
будет
выглядеть как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 1 отправить сообщение разработчикам Тема: Основные методы интегрирования
Начало формы
Конец формы
Множество
первообразных функции
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 2
отправить
сообщение разработчикам
Тема:
Свойства определенного интеграла
Начало формы
Конец формы
Значение
определенного интеграла
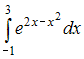принадлежит
промежутку …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Если
функция
интегрируема
на
и
то
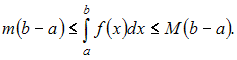Определим
наименьшее и наибольшее значения функции
на
отрезке
.
Для этого вычислим производную
и
решим уравнение
Тогда
Вычислив
и
получаем
наименьшее значение
а
наибольшее –
Следовательно,
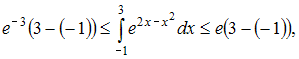или
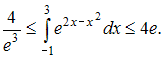
ЗАДАНИЕ N 3
отправить
сообщение разработчикам
Тема:
Методы вычисления определенного
интеграла
Начало формы
Конец формы
Определенный
интеграл
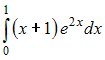равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Для
вычисления данного определенного
интеграла применим формулу интегрирования
по частям:
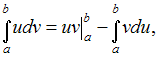где
Тогда
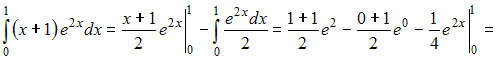
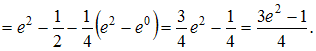
ЗАДАНИЕ
N 4
отправить
сообщение разработчикам
Тема:
Приложения определенного интеграла
Начало формы
Конец формы
Площадь
фигуры, ограниченной параболой
и
осью Ох,
равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 5
отправить
сообщение разработчикам
Тема:
Числовые последовательности
Начало формы
Конец формы
Числовая
последовательность задана рекуррентным
соотношением
Тогда
равно …
|
|
|
|
– 8 |
|
|
|
|
– 20 |
|
|
|
|
4 |
|
|
|
|
– 7 |
Решение:
Вычислим
последовательно:
ЗАДАНИЕ
N 6
отправить
сообщение разработчикам
Тема:
Сходимость числовых рядов
Начало формы
Конец формы
Сумма
числового ряда
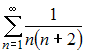равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ
N 7
отправить
сообщение разработчикам
Тема:
Область сходимости степенного ряда
Начало формы
Конец формы
Радиус
сходимости степенного ряда
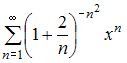равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ
N 8
отправить
сообщение разработчикам
Тема:
Ряд Тейлора (Маклорена)
Начало формы
Конец формы
Если
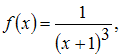то
коэффициент
разложения
данной функции в ряд Маклорена равен …
|
|
|
|
– 10 |
|
|
|
|
10 |
|
|
|
|
6 |
|
|
|
|
– 6 |
ЗАДАНИЕ N 9
отправить
сообщение разработчикам
Тема:
Типы дифференциальных уравнений
Начало формы
Конец формы
Уравнение
является …
|
|
|
|
линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами |
|
|
|
|
линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами |
|
|
|
|
дифференциальным уравнением второго порядка, допускающим понижение порядка |
|
|
|
|
уравнением Бернулли |
Решение:
Уравнение
можно
представить в виде
где
Следовательно,
данное уравнение является линейным
неоднородным дифференциальным уравнением
второго порядка с постоянными
коэффициентами.
ЗАДАНИЕ N 10
отправить
сообщение разработчикам
Тема:
Дифференциальные уравнения с разделяющимися
переменными
Начало формы
Конец формы
Общий
интеграл дифференциального уравнения
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Разделим
переменные в исходном уравнении:
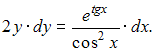Проинтегрируем
обе части уравнения:
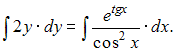Тогда
ЗАДАНИЕ N 11
отправить
сообщение разработчикам
Тема:
Линейные неоднородные дифференциальные
уравнения первого порядка
Начало формы
Конец формы
Общее
решение дифференциального уравнения
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
