Глава 2 Нарушениегипотезосновной линейноймодели

2.1. Обобщенныйметоднаименьшихквадратов (взвешеннаярегрессия)

Пусть нарушена гипотеза g4 и матрица ковариации ошибок по наблюдениям равна не σ²I_N, а σ²Ω, где Ω — вещественная симметричная положительно полуопределенная матрица (см. Приложение A.1.2), т.е. ошибки могут быть коррелированы по наблюдениям и иметь разную дисперсию. В этом случае обычные МНК-оценки параметров регрессии (1.26) остаются несмещенными и состоятельными, но перестают быть эффективными в классе линейных несмещенных оценок. Ковариационная матрица оценок МНК в этом случае приобретает вид

Действительно, a − E(a) = a − α = (Z"Z)−¹ Z"ε, поэтому

(Ср. с выводом формулы (1.28), где Ω = σ²I.)

Обычная оценка ковариационной матрицы s²_e (Z!Z)−¹ при этом является смещенной и несостоятельной. Как следствие, смещенными и несостоятельными оказываются оценки стандартных ошибок оценок параметров (1.35): чаще всего они преуменьшаются (т.к. ошибки по наблюдениям обычно коррелированы положительно), и заключения о качестве построенной регрессии оказываются неоправданно оптимистичными.

По этим причинам желательно применятьобобщенный МНК (ОМНК), заключающийся в минимизации обобщенной остаточной дисперсии

В обобщенной остаточной дисперсии остатки взвешиваются в соответствии со структурой ковариационной матрицы ошибок. Минимизация приводит к получению следующего оператора ОМНК-оценивания (ср. с (1.13), где Ω = I_N):

(2.1)

Для обоснования ОМНК проводится преобразование в пространстве наблюдений с помощью невырожденной матрицы D размерности N × N, такой, что (такое представление допускает любая вещественная симметричная положительно определенная матрица:

DX = DZα + Dε. (2.2)

Такое преобразование возвращает модельв «штатную» ситуацию, поскольку новые остатки удовлетворяют гипотезе g4:

Остаточная дисперсия теперь записывается как , а оператор оценивания — как

Что и требовалось доказать, поскольку .

Обычно ни дисперсии, ни тем более ковариации ошибок по наблюдениям не известны. В классической эконометрии рассматриваются два частных случая.

2.2. Гетероскедастичностьошибок

Пусть ошибки не коррелированы по наблюдениям, и матрица Ω (а вслед за ней и матрица D) диагональна. Если эта матрица единична, т.е. дисперсии ошибок одинаковы по наблюдениям (гипотеза g4 не нарушена), то имеет место гомоскедастичность или однородность ошибок по дисперсии — «штатная» ситуация. В противном случае констатируют гетероскедастичность ошибок или их неоднородность по дисперсии.

Пусть var(ε_i) = σ_i² — дисперсия ошибки i-го наблюдения. Гомоскедастичность означает, что все числа σ_i² одинаковы, а гетероскедастичность — что среди них есть несовпадающие.

Факт неоднородности остатков по дисперсии мало сказывается на качестве оценок регрессии, если эти дисперсии не коррелированы с независимыми факторами. Это — случай гетероскедастичности «без негативных последствий».

Данное утверждение можно проиллюстрировать в случае, когда в матрице

Z всего один столбец, т.е. n = 1 и свободный член отсутствует. Тогда формула (1.33) приобретает вид:

.

Еслиситуацияштатнаяи σ_i² = σ²,то правая часть этой формулы преобразуется к виду 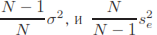оказывается несмещенной оценкойσ², как и было показано впараграфе 1.2. Если σ_i и z_i не коррелированы, то, обозначив, можно утверждать, что

т.е. ситуация остается прежней. И только если σ_i и z_i положительно (или отрицательно) коррелированы, факт гетероскедастичности имеет негативные последствия.

Действительно, в случае положительной корреляции и, следовательно,. Обычная «несмещенная» оценка остаточной дисперсии оказывается по математическому ожиданию меньше действительного значения остаточной дисперсии, т.е. она (оценка остаточной дисперсии) дает основания для неоправданно оптимистичных заключений о качестве полученной оценки модели.

Следует заметить, что факт зависимости дисперсий ошибок от независимых фактороввэкономикевесьмараспространен.В экономике одинаковыми по дисперсии скорее являются относительные (ε"z), а не абсолютные (ε) ошибки. Поэтому, когда оценивается модель на основе данных по предприятиям, которые могут иметь и, как правило, имеют различные масштабы, гетероскедастичности с негативными последствиями просто не может не быть.

Если имеет место гетероскедастичность, то, как правило, дисперсия ошибки связана с одной или несколькими переменными, в первую очередь — с факторами регрессии. Пусть, например, дисперсия может зависеть от некоторой переменной y_i, которая не является константой:

Как правило, в качестве переменной y_i берется один из независимых факторов или математическое ожидание изучаемой переменной, т.е. x⁰ = Zα (в качестве его оценки используют расчетные значения изучаемой переменной Za).В этой ситуации желательно решить две задачи: во-первых, определить, имеет лиместопредполагаемаязависимость,аво-вторых,еслизависимость обнаружена, получить оценки с ее учетом. При этом могут использоваться три группы методов. Методы первой группы позволяют работать с гетероскедастичностью, которая задается произвольной непрерывной функцией σ²(·). Для методов второй группы²(·) функция σ²(·) должна быть монотонной. В методах третьей группы функция σ предполагается известной с точностью до конечного числа параметров.

Примером метода из первой группы является критерий Бартлетта, который заключается в следующем.

Пусть модель оценена и найдены остатки e_i, i = 1, ..., N. Для расчета b^c — статистики, лежащей в основе применения этого критерия, все множество наблюдений делится по какому-либо принципу на k непересекающихся подмножеств. В частности, если требуется выявить, имеется ли зависимость от некоторой переменной y_i, то все наблюдения упорядочиваются по возрастанию y_i, а затем в соответствии с этим порядком делятся на подмножества. Пусть

N_l — количество элементов в l-м подмножестве,

s²_l — оценка дисперсии остатков в l-м подмножестве, найденная на основе

остатков e_i;

- отношение средней арифметической дисперсий к средней геометрической; это отношение в соответствии со свойством мажорантности средних больше или равно единице, и чем сильнее различаются дисперсии по подмножествам, тем оно выше.

Тогда статистика Бартлетта равна

.

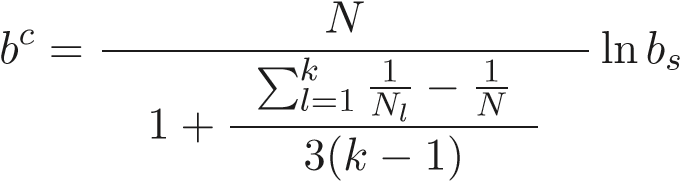При однородности наблюдений по дисперсии (нулевая гипотеза) эта статистика распределена как χ²_k−1. Проверка нулевой гипотезы проводится по обычному алгоритму._.

Если нулевую гипотезу отвергнуть не удалось, т.е. ситуация гомоскедастична, то исходная оценка модели удовлетворительна. Если же нулевая гипотеза отвергнута, то ситуация гетероскедастична.

Принцип построения статистики Бартлетта иллюстрирует рисунок 2.1.

Классическийметод второйгруппызаключаетсявследующем.Всенаблюдения упорядочиваются по возрастанию некоторой переменной y_i. Затем оцениваются две вспомогательные регрессии: по K «малым» и по K «большим»наблюдениям

(не участвуютс целью повышения мощности критерия средние, а K можно, например, выбрать равным приблизительно третиN − 2K наблюдения в расчетеN).

Пусть s²₁ — остаточная дисперсия в первой из этих регрессий, а s²₂ — во второй. Вслучаегомоскедастичностиошибок(нулеваягипотеза)отношениедвухдисперсий распределено как

.

Здесь следует применять обычный F-критерий. Нулевая гипотеза о гомоскедастичности принимается, если рассчитанная статистика превышает 95%-ный квантиль F-распределения.

Рис. 2.2

Такой подход применяется, если ожидается, что дисперсия может быть только положительно коррелирована с переменной y_i. Если неизвестно, положительно или отрицательно коррелирована дисперсия с рассматриваемым фактором, то следует отклонять нулевую гипотезу как при больших, так и при малых значениях статистики ^s22"_s21. Можно применить следующий прием: рассчитать статистику как отношение максимальной из дисперсий s²₁ и s²₂ к минимальной. Такая статистика будет иметь усеченное F-распределение, где усечение происходит на уровне медианы, и берется правая половина распределения. Отсюда следует, что для достижения, например, 5%-го уровня ошибки, следует взять табличную критическуюграницу,соответствующую, 2.5%-муправомухвостуобычного(неусеченного) F-распределения. Если указанная статистика превышает данную границу, то нулевая гипотеза о гомоскедастичности отвергается.

Данный метод известен под названием метода Голдфельда—Квандта. Можно применять упрощенный вариант этого критерия, когда дисперсии s²₂ и s²₂ считаются на основе остатков из проверяемой регрессии. При этом s²₁ и s²₂ не будут независимы, и их отношение будет иметь F-распределение только приближенно. Этот метод иллюстрирует рисунок 2.2.

Для того чтобы можно было применять методы третьей группы, требуется обладать конкретной информацией о том, какой именно вид имеет гетероскедастичность.

Так, например, если остатки прямо пропорциональны значениям фактора (n = 1):

x = zα + β + zε,

и ε удовлетворяет необходимым гипотезам, то делением обеих частей уравнения на z ситуация возвращается в «штатную»:

,

Рис. 2.3

в которой, правда, угловой коэффициент и свободный член меняются местами. Тем самым применяется преобразование в пространстве наблюдений такое, что диагональные элементы матрицы D равны 1"z_i .

Если зависимость дисперсии от других переменных известна не точно, а только с точностью до некоторых неизвестных параметров, то для проверки гомоскедастичности следует использовать вспомогательные регрессии.

Так называемый метод Глейзера состоит в следующем. Строится регрессия модулей остатков |eⁱ| на константу и те переменные, которые могут быть коррелированными с дисперсией (например, это _{может быть все множество независимых} факторов или какое-то их подмножество). Если регрессия оказывается статистически значимой, то гипотеза гомоскедастичности отвергается.

Построение вспомогательной регрессии от некоторой переменной y_i показано на рисунке 2.3.

Другой метод (критерий Годфрея) использует аналогичную вспомогательную регрессию, в которой в качестве зависимой переменной используются квадраты остатков e²_i .

Если с помощью какого-либо из перечисленных критериев (или других аналогичных критериев) проверены различные варианты возможной зависимости и нулевая гипотеза во всех случаях не была отвергнута, то делается вывод, что ситуация гомоскедастична или гетероскедастична без негативных последствий и что для оценки параметров модели можно использовать обычный МНК. Если же нулевая гипотеза отвергнута и поэтому, возможно, имеет место гетероскедастичность с негативными последствиями, то желательно получить более точные оценки, учитывающие гетероскедастичность.

Это можно сделать, используя для оценивания обобщенный МНК (см. уравнение (2.2)). Соответствующее преобразование в пространстве наблюдений состоит

в том, чтобы каждое наблюдение умножить на d_i, т.е. требуется оценить обычным методом наименьших квадратов преобразованную регрессию с переменными d_iX_i и d_iZ_i. При этом не следует забывать, что если матрица факторов Z содержит свободный член, то его тоже нужно умножить на d_i, поэтому вместо свободного члена в регрессии появится переменная вида (d₁, ..., d_N). Это приводит к тому, что стандартные статистические пакеты выдают неверные значения коэффициента детерминации и F-статистики. Чтобы этого не происходило, требуется пользоваться специализированными процедурами для расчета взвешенной регрессии. Описанный методполучил названиевзвешенногоМНК, посколькуон равнозначен

N минимизации взвешенной суммы квадратов остатков % d²_i e²_i .

i=1

Чтобы это можно было осуществить, необходимо каким-то образом получить оценкуматрицы D,используемойдляпреобразованиявпространственаблюдений. Перечисленные в этом параграфе методы дают возможность не только проверить гипотезу об отсутствии гетероскедастичности, но и получить определенные оценки матрицы D (возможно, не очень хорошие).

Если S² — оценка матрицы σ²Ω , где S² — диагональная матрица, составленная из оценок дисперсий, то S−¹ (матрица, обратная к ее квадратному корню) — оценка матрицы σD.

Так, после проверки гомоскедастичности методом Глейзера в качестве диагональных элементов матрицы| | S−¹ можно взять 1"|_ei|c , где |e_i|^c — расчетные значения e_i . Если используются критерии Бартлетта или Голдфельда—Квандта, то наблюдения разбиваются на группы, для каждой из которых есть оценка дисперсии, s²_l . Тогда для этой группы наблюдений в качестве диагональных элементов матрицы S−¹ можно взять 1"s_l .

В методе Голдфельда—Квандта требуется дополнительно получить оценку дисперсии для пропущенной средней части наблюдений. Эту оценку можно получить непосредственнопоостаткампропущенныхналюденийиликаксреднее (s²₁+s²₂)/2.

Если точный вид гетероскедастичности неизвестен, и, как следствие, взвешенный МНК неприменим, то, по крайней мере, следует скорректировать оценку ковариационной матрицы оценок параметров, оцененных обычным МНК, прежде чем проверять гипотезы о значимости коэффициентов. (Хотя при использовании обычного МНКоценки будутменее точными, нокакужеупоминалось, онибудут несмещенными и состоятельными.) Простейший метод коррекции состоит в замене неизвестной ковариационной матрицы ошибок σ²Ω на ее оценку S², где S² — диагональная матрица стипичнымэлементом e²_i (т.е.квадратыостатковиспользуютсякакоценки дисперсий). Тогда получается следующая скорректированная оценка ковариационной матрицы a (оценкаУайта или устойчиваякгетероскедастичностиоценка):

(Z"Z)−1 Z"S2Z (Z"Z)−1 .

2.3. Автокорреляцияошибок

Если матрица ковариаций ошибок не является диагональной, то говорят об автокорреляции ошибок. Обычно при этом предполагают, что наблюдения однородны по дисперсии, и их последовательность имеет определенный смысл и жестко фиксирована. Как правило, такая ситуация имеет место, если наблюдения проводятся в последовательные моменты времени. В этом случае можно говорить о зависимостях ошибок по наблюдениям, отстоящим друг от друга на 1, 2, 3 и т.д. моментавремени.Обычнорассматриваетсячастныйслучайавтокорреляции,когда коэффициенты ковариации ошибок зависят только от расстояния во времени между наблюдениями; тогда возникает матрица ковариаций, в которой все элементы каждой диагонали (не только главной) одинаковы¹.

Поскольку действие причин, обуславливающих возникновение ошибок, достаточноустойчивововремени,автокорреляцииошибок,какправило,положительны. Это ведет к тому, что значения остаточной дисперсии, полученные по стандартным («штатным») формулам, оказываются ниже их действительных значений. Что, как отмечалось и в предыдущем пункте, чревато ошибочными выводами о качестве получаемых моделей.

Это утверждение иллюстрируется рисунком 2.4 (n = 1).

На этом рисунке:

a — линия истинной регрессии. Если в первый момент времени истинная ошибка отрицательна, то в силу положительной автокорреляции ошибок все облако наблюдений сместится вниз, и линия оцененной регрессии займет положение b. Есливпервыймоментвремениистиннаяошибкаположительна, топотемжепричинам линия оцененной регрессии сместится вверх и займет положение c. Поскольку

¹В теории временных рядов это называется слабой стационарностью.

Рис. 2.4

ошибки случайны и в первый момент времени они примерно с равной вероятностью могут оказаться положительными или отрицательными, то становится ясно, насколько увеличивается разброс оценок регрессии вокруг истинных по сравнению с ситуацией без (положительной) автокорреляции ошибок.

Типичный случай автокорреляции ошибок, рассматриваемый в классической эконометрии, — это линейная авторегрессия ошибок первого порядка AR(1):

ε_i = ρε_i−1 + η_i,

где η — остатки, удовлетворяющие обычным гипотезам; ρ — коэффициент авторегрессии первого порядка.

Коэффициент ρ вляется также коэффициентом автокорреляции (первого порядка).

Действительно, по определению, коэффициент авторегрессии равен (как МНКоценка):

cov(εi,εi−1), ρ =

var(ε_i−1)

но, в силу гомоскедастичности, var(ε_i−1) = Zvar(ε_i)var(ε_i−1) и, следовательно, ρ, также по определению, является коэффициентом автокорреляции.

Если ρ = 0, то ε_i = η_i и получаем «штатную» ситуацию. Таким образом, проверку того, что автокорреляция отсутствует, можно проводить как проверку нулевой гипотезы H₀: ρ = 0 для процесса авторегрессии 1-го порядка в ошибках.

Для проверки этой гипотезы можно использовать критерий Дарбина— Уотсона или DW-критерий. Проверяется нулевая гипотеза о том, что автокорреляция ошибок первого порядка отсутствует. (При автокорреляции второго и более высоких порядков его мощность может быть мала, и применение данного критерия становится ненадежным.)

Пусть была оценена модель регрессии и найдены остатки e_i, i = 1, ..., N. Значение статистики Дарбина—Уотсона (отношения фон Неймана), или DW-статистики, рассчитывается следующим образом:

. (2.3)

Оно лежит в интервале от 0 до 4, в случае отсутствия автокорреляции ошибок приблизительно равно 2, при положительной автокорреляции смещается в мень-

d_L d_U 4&d_U 4&d_L

Рис. 2.5

шую сторону, при отрицательной — в большую сторону. Эти факты подтверждаются тем, что при больших N справедливо следующее соотношение:

d^c ≈ 2(1 − r), (2.4)

где r — оценка коэффициента авторегрессии.

Минимального значения величина d^c достигает, если коэффициент авторегрессии равен +1. В этом случае e_i = e, i = 1, ..., N, и d^c = 0. Если коэффициент авторегрессии равен −1 и e_i = (−1)ⁱe, i = 1, ..., N, то величинаd^c достигает значения (можно достичь и более высокого значения подбором остатков), которое с ростомN стремится к 4. Формула (2.4) следует непосредственно из (2.3) после элементарных преобразований:

,

поскольку первое и третье слагаемые при больших N близки к единице, а второе слагаемое является оценкой коэффициента автокорреляции (умноженной на −2).

Известно распределение величины d, если ρ = 0 (это распределение близко к нормальному), но параметры этого распределения зависят не только от N и n, как для t- и F-статистик при нулевых гипотезах. Положение «колокола» функции плотности распределения этой величины зависит от характера Z. Тем не менее, ДарбиниУотсонпоказали,чтоэтоположениеимеетдвекрайниепозиции(рис.2.5).

Поэтому существует по два значения для каждого (двустороннего) квантиля, соответствующего определенным N и n: его нижняя d_L и верхняя d_U границы. Нулевая гипотеза H₀: ρ = 0 принимается, если d_U ! d^c ! 4−d_U ; она отвергается в пользу гипотезы о положительной автокорреляции, если d^c < d_L, и в пользу гипотезы об отрицательной автокорреляции, если. Если d_L ! d^c < d_U

DWили-4критерия−d_U < d).^c ! 4−d_L,вопросостаетсяоткрытым зонанеопределенности

Пусть нулевая гипотеза отвергнута. Тогда необходимо дать оценку матрицы Ω.

Оценка r параметра авторегрессии ρ может определяться из приближенного равенства, следующего из (2.4):

,

или рассчитываться непосредственно из регрессии e на него самого со сдвигом на одно наблюдение с принятием «круговой» гипотезы, которая заключается в том, что eN+1 = e1.

Оценкой матрицы Ω является

,

а матрица D преобразований в пространстве наблюдений равна

.

Для преобразования в пространстве наблюдений, называемом в данном случае авторегрессионным, используют обычно указанную матрицу без 1-й строки, что ведет к сокращению количества наблюдений на одно. В результате такого преобразования из каждого наблюдения, начиная со 2-го, вычитается предыдущее, умноженное на r, теоретическими остатками становятся η , которые, по предположению, удовлетворяют гипотезе g4.

После этого преобразования снова оцениваются параметры регрессии. Если новое значение DW-статистики неудовлетворительно, то можно провести следующее авторегрессионное преобразование.

Обобщает процедуру последовательных авторегрессионных преобразований метод Кочрена—Оркатта, который заключается в следующем.

Для одновременной оценки r, a и b используется критерий ОМНК (в обозначениях исходной формы уравнения регрессии):

,

где z_i — n-вектор-строка значений независимых факторов в i-м наблюдении (i-строка матрицы Z).

Поскольку производные функционала по искомым величинам нелинейны относительно них, применяется итеративная процедура, на каждом шаге которой сначала оцениваются a и b при фиксированном значении r предыдущего шага (на первом шаге обычно r = 0), а затем — r при полученных значениях a и b. Процесс, как правило, сходится.

Как и в случае гетероскедастичности, можно не использовать модифицированные методы оценивания (тем более, что точный вид автокорреляции может быть неизвестен), а использовать обычный МНК и скорректировать оценку ковариационной матрицы параметров. Наиболее часто используемая оценкаНьюи—Уэста (устойчивая к гетероскедастичности и автокорреляции) имеет следующий вид:

(Z"Z)−¹ Q(Z"Z)−¹ ,

где

,

а λ_k — понижающие коэффициенты, которые Ньюи и Уэст предложили рассчитывать по формуле . Приk > L понижающие коэффициенты становятся равными нулю, т.е. более дальние корреляции не учитываются Обоснование этой оценки достаточно сложно¹. Заметим только, что если заменить попарные произведения остатков соответствующими ковариациями и убрать понижающие коэффициенты, то получится формула ковариационной матрицы оценок МНК.

Приведенная оценка зависит от выбора параметра отсечения L. В настоящее время не существует простых теоретически обоснованных методов для такого выбора. На практике можно ориентироваться на грубое правило L = <4(T"100)^2/9=.

2.4. Ошибкиизмеренияфакторов

Пусть теперь нарушается гипотеза g2, и независимые факторы наблюдаются с ошибками. Предполагается, что изучаемая переменная зависит от истинных значений факторов (далее в этом пункте используется сокращенная форма уравнения регрессии), zˆ⁰, а именно:

xˆ = zˆ⁰α + ε,

но истинные значения неизвестны, а вместо этого имеются наблюдения над некоторыми связанными с zˆ⁰ переменными zˆ:

zˆ = zˆ⁰ + ε_z,

где ε_z — вектор-строка длиной n ошибок наблюдений.

В разрезе наблюдений:

Xˆ = Zˆ⁰α + ε, Zˆ = Zˆ⁰ + ε_z,

где Zˆ₀ и ε^z — соответствующие N × n-матрицы значений этих величин по на, ε_z обозначает вектор или матрицублюдениям _(т.е_., в зависимости от контекста ошибок).

Предполагается, что ошибки факторов по математическому ожиданию равны нулю,истинныезначениярегрессоровиошибкинезависимыдруготдруга(покрайней мере не коррелированы друг с другом) и известны матрицы ковариации:

E(ε_z) = 0, E,

(2.5)

E.

Важно отметить, что эти матрицы и вектора ковариации одинаковы во всех наблюдениях, а ошибки в разных наблюдениях не зависят друг от друга, т.е. речь, фактически,идет о «матричной» гомоскедастичности и отсутствии автокорреляции ошибок.

Через наблюдаемые переменные xˆ и zˆ уравнение регрессии записывается в следующей форме:

xˆ = zˆα + ε − ε_zα. (2.6)

В такой записи видно, что «новые» остатки не могут быть независимыми от факторов-регрессоров zˆ, т.е. гипотезы основной модели регрессии нарушены. В рамках

можно доказать, что приближенно

E(a) ≈ (M⁰ + Ω)−¹(M⁰α + ω) = α + (M⁰ + Ω)−¹(ω − Ωα), (2.7) т.е. МНК-оценки теряют в такой ситуации свойства состоятельности и несмещенности², еслиω =! Ωα (в частности, когда ошибки регрессии и ошибки факторов не коррелированны, т.е. когда ω = 0, а Ω и α отличны от нуля).

Для обоснования (2.7) перейдем к теоретическому аналогу системы нормальных уравнений, для чего обе части соотношения (2.6) умножаются на транспонированную матрицу факторов:

E(zˆ"xˆ) = E(zˆ"zˆ)α + E(zˆ"ε) − E(zˆ"ε_z)α.

Здесь, как несложно показать, пользуясь сделанными предположениями,

E(zˆ"zˆ) = M⁰ + Ω,

E(zˆ"ε) = ω,

E(zˆ"ε_z) = Ω,

Поэтому

E(zˆ"xˆ) = E(zˆ"zˆ)α + ω − Ωα

или

E(zˆ"zˆ)−¹E(zˆ"xˆ) = α + 0M⁰ + Ω1⁻¹ (ω − Ωα).

Левая часть приближенно равна E(a).

Действительно, a = M−¹m, где M ⁼ _N¹ Z^ˆ"Z^ˆ и m ⁼ _N¹ Z^ˆ"xˆ. Выборочные ковариационные матрицы M и m по закону больших чисел с ростом числа наблюдений сходятся по вероятности к своим теоретическим аналогам:

p и m −→E(zˆ"xˆ).

Посвойствамсходимостиповероятностипределфункцииравенфункцииотпредела, если функция непрерывна. Поэтому

.

Существуют разные подходы к оценке параметров регрессии в случае наличия ошибок измерения независимых факторов. Здесь приводятся два из них.

а) Простая регрессия. Если имеется оценка W ковариационной матрицы Ω и w — ковариационного вектора ω , то можно использовать следующий оператор оценивания:

a = (M − W)−¹(m − w),

который обеспечивает состоятельность оценок и делает их менее смещенными.

Это формула следует из

E(zˆ"xˆ) = E(zˆ"zˆ)α + ω − Ωα

заменой теоретических моментов на их оценки.

Обычно предполагается, что W — диагональная матрица, а w = 0.

б) Ортогональная регрессия. Поскольку z теперь такие же случайные переменные,наблюдаемыесошибками,каки x,имеетсмыслвернутьсякобозначениям 6-го раздела, где через x обозначался n-мерный вектор-строка всех переменных. Пусть ε — вектор их ошибок наблюдения, а x⁰ — вектор их истинных значений, то есть

x = x⁰ + ε, X = X⁰ + ε.

Предположения (2.5) записываются следующим образом:

E.

Теперь через M⁰ обозначается матрица, которую в обозначениях, используемых в этом пункте выше, можно записать следующим образом:

,

а через σ²Ω матрица

.

Поскольку речь идет о линейной регрессии, предполагается, что между истинными значениями переменных существует линейная зависимость:

x⁰α = 0.

Это означает, что

M⁰α = 0.

Рассуждаятакже,какпридоказательствесоотношения(2.7),легкоустановить, что

E(M) = M⁰ + σ²Ω,

(M — фактическая матрица ковариации X) т.е.

(E(M) − σ²Ω)α = 0.

Таким образом, если считать, что Ω известна, а σ² — минимизируемый параметр

(в соответствии с логикой МНК), то решение задачи

(M − σ²Ω)a = 0, σ² → min!

даст несмещенную оценку вектора α . А это, как было показано в пункте 6.4, есть задача регрессии в метрике Ω−¹ (см. (6.37)). Преобразованием в пространстве переменных она сводится к «обычной» ортогональной регрессии.

Т.е. если для устранения последствий нарушения гипотезы g4 используется преобразование в пространстве наблюдений, то при нарушении гипотезы g2 надо «работать» с преобразованием в пространстве переменных.

Несмотря на то, что методы ортогональной регрессии и регрессии в метрике Ω−¹ внаибольшейстепенисоответствуютреалиямэкономики(ошибкиестьвовсех переменных, стоящих как в левой, так и в правой частях уравнения регрессии), они мало используются в прикладных исследованиях. Основная причина этого заключается в том, что в большинстве случаев невозможно получить надежные оценки матрицы Ω. Кроме того, ортогональная регрессия гораздо сложнее простой с вычислительной точки зрения,и стеоретической точки зренияона существенно менее изящна и прозрачна.

Вследующемпараграфеизлагаетсяещеодинметод,которыйпозволяетрешить проблему ошибок в переменных (и в целом может использоваться при любых нарушениях гипотезы g2).

2.5. Методинструментальныхпеременных

Предполагаем, что в регрессии x = zα + ε переменные-факторы z являются случайными,инарушенагипотезаg2вобобщеннойформулировке:ошибка ε зависит от факторов z, так что корреляция между z и ошибкой ε не равна нулю. Такую регрессию можно оценить, имея набор вспомогательных переменных y, называемых инструментальными переменными. Часто инструментальные переменные называют просто инструментами.

Для того, чтобы переменные y можно было использовать в качестве инструментальных, нужно, чтобы они удовлетворяли следующим требованиям:

Инструменты y некоррелированы с ошибкой ε. (В противном случае метод даст несостоятельные оценки, как и МНК.) Если это условие не выполнено, то такие переменные называют негодными инструментами⁴.

Инструменты y достаточно сильно коррелированы с факторами z. Если данное условие не выполнено, то это так называемые «слабые» инструменты. Если инструменты слабые, то оценки по методу будут неточными и при малом количестве наблюдений сильно смещенными.

Обычно z и y содержатобщиепеременные,т.е.частьфакторовиспользуетсяв качествеинструментов.Например,типичнаситуация,когда z содержитконстанту; тогда в y тоже следует включить константу.

Пусть имеются N наблюдений, и X, Z и Y — соответствующие данные в матричном виде. Оценки по методу инструментальных переменных (сокращенно IV от англ. instrumental variables) вычисляются по следующей формуле:

a_IV = (Z!Y 0Y !Y 1−¹ Y !Z)−¹ Z!Y 0Y !Y 1−¹ Y !X. (2.8)

В случае, если количество инструментальных переменных в точности равно количеству факторов, (rankY = n + 1) получаем собственно классический метод инструментальных переменных. При этом матрица Y !Z квадратная и оценки вычисляются как

a_IV = 0Y !Z1−¹ Y !Y 0Z!Y 1−¹ Z!Y 0Y !Y 1−¹ Y !X.

Средняя часть формулы сокращается, поэтому

a_IV = 0Y !Z1−¹ Y !X. (2.9)

Рассмотрим вывод классического метода инструментальных переменных,

т.е. случай точной идентификации (ср. с (6.15) в главе 6):

Умножим уравнение регрессии x = zα + ε слева на инструменты y (с транспонированием). Получим следующее уравнение:

y!x = y!zα + y!ε.

исходном уравнении⁴В модели ошибок в переменных ошибка регрессии имеет вид, а εz — ошибка измерения факторов z. Чтобы переменныеε−ε_zα, где εy —можно былоошибка в использовать в качестве инструментов, достаточно, чтобы y были некоррелированы с ε и ε_z.

Если взять от обеих частей математическое ожидание, то получится

E(y!x) = E(y!zα),

где мы учли, что инструменты некоррелированы с ошибкой, E(y!ε) = 0.

Заменяятеоретическиемоментынавыборочные,получимследующиенормальные уравнения, задающие оценки a:

Myx = Myza,

где M_yx ⁼ _N¹ Y !X и M_yz ⁼ _N¹ Y !Z. Очевидно, что эти оценки совпадут с (2.9). Фактически, мы применяем здесь метод моментов.

Метод инструментальных переменных можно рассматривать как так называемый двухшаговый метод наименьших квадратов. (О нем речь еще пойдет ниже в пункте 10.3.)

1-й шаг. Строим регрессию каждого фактора Z_j на Y . Получим в этой регрессии расчетный значения Z_j^c. По формуле расчетных значений в регрессии Z_j^c = Y (Y !Y )−¹ Y !Z. Заметим, что если Z_j входит в число инструментов, то по этой формуле получим . эта переменная останется без изменений. Поэтому данную процедуру достаточно применять только к тем факторам, которые не являются инструментами (т.е. могут быть коррелированы с ошибкой). В целом для всей матрицы факторов можем записатьZ^c = Y (Y !Y )−¹ Y !Z.

2-й шаг. В исходной регрессии используются Z^c вместо Z. Смысл состоит в том, чтобы использовать факторы «очищенные от ошибок».

Получаем следующие оценки: a_2M = 0Z^c!Z^c1−¹ Z^c!x =

= (Z!Y 0Y !Y 1−¹ Y !Y 0Y !Y 1−¹ Y !Z)−¹ Z!Y 0Y !Y 1−¹ Y !x =

= (Z!Y 0Y !Y 1−¹ Y !Z)−¹ Z!Y 0Y !Y 1−¹ Y !x = a_IV .

Видим, что оценки совпадают.

Если записать оценки в виде a_IV = (Z^c!Z)−¹ Z^c!x, то видно, что обобщенный метод инструментальных переменных можно рассматривать как простой метод инструментальных переменных с матрицей инструментов Z^c.

Такая запись позволяет обосновать обобщенный метод инструментальных переменных. Если исходных инструментов Y больше, чем факторов Z, и мы хотим построить на их основе меньшее количество инструментов, то имеет смысл сопоставить каждому фактору Z_j вкачестве инструмента такуюлинейную комбинацию исходных инструментов, которая была бы наиболее сильно коррелирована с Z_j. Этому требованию как раз и удовлетворяют расчетные значения Z_j^c.

Другое обоснование обобщенного метода инструментальных переменных состоит, как и выше для классического метода, в использовании уравнений E(y!x) = = E(y!zα). Заменой теоретических моментов выборочными получим уравнения M_yx = M_yza, число которыхбольшечисла неизвестных. Идея состоит втом, чтобы невязки M^yx − M^yza были как можно меньшими. Это достигается минимизацией следующей квадратичной формы от невязок:

(Myx − Myza)!Myy−1(Myx − Myza),

где M_yy ⁼ _N¹ Y !Y . Минимум достигается при

a = (MzyMyy−1Myz)−1 MzyMyy−1Myx.

Видим, что эта формула совпадает с (2.8). Эти рассуждения представляют собой применение так называемого обобщенного метода моментов, в котором количество условий на моменты может превышать количество неизвестных параметров.

Чтобы можно было использовать метод инструментальных переменных на практике, нужна оценка ковариационной матрицы, с помощью которой можно было бы вычислить стандартные ошибки коэффициентов и t-статистики. Такая оценка имеет вид

MaIV = s20Zc!Zc1−1 .

Здесь s² — оценка дисперсии ошибок σ², например s² = e!e/N или s² =

= e!e/(N − 1). Остатки рассчитываются по обычной формуле, что остатки, получаемые на втором шаге тут не годятe = x − ZaIV-.

(Здесь следует помнить

ся, поскольку они равны x − Z^ca^IV . Если использовать их для расчета оценкиу дисперсии и ковариационной матрицы. дисперсии, то получим заниженную оценк

Отсюда следует, что из регрессии второго шага можно использовать только оценки коэффициентов. Стандартные ошибки и t-статистики требуется пересчитывать.) Обсудим теперь более подробно проблему идентификации³.

Чтобы можно было вычислить оценки (2.8), нужно, чтобы выполнялись следующие условия:

Матрица инструментов должна иметь полный ранг по столбцам, иначе (Y !Y )−¹ не существует.

Z!Y (Y !Y )−¹ Y !Z должна быть невырожденной.