
- •Введение
- •Глава 1 Основная модель линейной регрессии
- •1.4. Прогнозирование
- •Рекомендуемаялитература
- •Глава 2 Нарушениегипотезосновной линейноймодели
- •2.1. Обобщенныйметоднаименьшихквадратов (взвешеннаярегрессия)
- •2.2. Гетероскедастичностьошибок
- •2.3. Автокорреляцияошибок
- •2.4. Ошибкиизмеренияфакторов
- •2.5. Методинструментальныхпеременных
- •1.2 Оценка Надарии-Уотсон
Глава 1 Основная модель линейной регрессии
1.1. Различные формы уравнения регрессии
Основная модель линейной регрессии относится к классу простых регрессий, в левой части уравнения которых находится одна переменная: объясняемая, моделируемая, эндогенная, а в правой — несколько переменных: объясняющих, факторных, независимых, экзогенных. Объясняющие переменные называют также факторами, регрессорами.
Для объясняемой переменной сохраняется прежнее обозначение — x. А вектор-строка размерности n объясняющих переменных будет теперь обозначаться через z, поскольку свойства этих переменных в основной модели регрессии существенно отличаются от свойств объясняемой переменной. Через X и Z обозначаются, соответственно, вектор-столбец размерности N наблюдений за объясняемой переменной и матрица размерности N х n наблюдений за объясняющими переменными. Обозначения параметров регрессии и остатков по наблюдениям сохраняются прежними (отличие в том, что теперь вектор-столбцы а и а имеют размерность n).
Уравнения регрессии в исходной форме имеют следующий вид:
X
= Za
+ 1N
 +
+ (1.1)
(1.1)
или в оценках
X = Za + 1N b + e. (1.2)
В сокращенной форме:
 =
=
 a
+
a
+ , (1.3)
, (1.3)
или
 =
=
 a
+ e. (1.4)
a
+ e. (1.4)
Оператор МНК-оценивания принимает вид:
 b=
b= (1.5)
(1.5)
где
M = ковариационная матрица переменных z
между собой,
m
=
ковариационная матрица переменных z
между собой,
m
= —
вектор ковариаций переменных z с
переменной x. Первую часть оператора
(1.5)
часто записывают в форме:
—
вектор ковариаций переменных z с
переменной x. Первую часть оператора
(1.5)
часто записывают в форме:
а
=
 (1.6)
(1.6)
МНК-оценки e обладают следующими свойствами :
 ,
cov(Z,e) =
,
cov(Z,e) =
 =
0. (1.7)
Коэффициент детерминации рассчитывается
следующим образом :
=
0. (1.7)
Коэффициент детерминации рассчитывается
следующим образом :
 (1.8)
(1.8)
где
 —
дисперсия объясняемой переменной,
—
дисперсия объясняемой переменной,
 —
остаточная дисперсия,
—
остаточная дисперсия,
 (1.9)
объясненная дисперсия.
(1.9)
объясненная дисперсия.
Уравнение регрессии часто записывают в форме со скрытым свободным членом:
X
= ,
(1.10)
,
(1.10)
X
=
 +e,
(1.11)
+e,
(1.11)
где

При таком представлении уравнения регрессии оператор МНК-оценивания записывается следующим, более компактным, чем (1.5), образом:
 (1.12)
(1.12)
где  ,
или
,
или
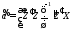 (1.13)
(1.13)
 и
и
 также,
как M и m, являются матрицей и вектором
вторых моментов, но не центральных, а
начальных. Кроме того, их размерность
на единицу больше.
также,
как M и m, являются матрицей и вектором
вторых моментов, но не центральных, а
начальных. Кроме того, их размерность
на единицу больше.
Оператор (1.12) дает, естественно, такой же результат, что и оператор (1.5).
В общем случае этот факт доказывается следующим образом. Учитывая, что
 (1.14)
(1.14)
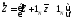 (1.15)
(1.15)
можно установить, что
 (1.16)
(1.16)

и записать систему нормальных уравнений, решением которой является (1.12) в следующей форме:

Вторая
(нижняя) часть этой матричной системы
уравнений эквивалентна второй части
оператора (1.5). После подстановки b,
выраженного через
 ,
в первую (верхнюю) часть данной матричной
системы уравнений она приобретает
следующий вид:
,
в первую (верхнюю) часть данной матричной
системы уравнений она приобретает
следующий вид:

и после приведения подобных становится очевидной ее эквивалентность первой части оператора (1.5).
Что и требовалось доказать. Кроме того, можно доказать, что
 (1.17)
(1.17)
Этот факт потребуется ниже. (Правило обращения блочных матриц см. в Приложении A.1.2.)
Справедливость
этого утверждения проверяется умножением
 из
(1.17) на
из
(1.17) на из (1.16). В результате получается единичная
матрица.
из (1.16). В результате получается единичная
матрица.
МНК-оценки
вектора e ортогональны столбцам матрицы
 :
:
 '
' = 0. (1.18)
= 0. (1.18)
Доказательство наличия этого свойства получается как побочный результат при вы -воде оператора оценивания (1.12) путем приравнивания нулю производных оста¬точной дисперсии по параметрам регрессии.
Поскольку
последним столбцом матрицы
 является
является ,
из (1.18) следует,что
,
из (1.18) следует,что
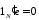 ,
(1.19)
,
(1.19)
т.е.
 = 0. Из остальной части (1.18):
= 0. Из остальной части (1.18):
Z'e
= 0, (1.20)
что в данном случае означает, что cov(Z,
 )
= 0. Действительно, раскрывая (1.20):
)
= 0. Действительно, раскрывая (1.20):
Z'e

Таким образом, (1.18) эквивалентно (1.7).
Однако
уравнения (1.10)
допускают и иную интерпретацию. Если
последним в
 является
не
является
не
 ,
а столбец «обычной» переменной, то это
— регрессия без свободного члена. В
таком случае из (1.18)
не следует (1.19),
и свойства (1.7)
не выполняются. Кроме того, для такой
регрессии, очевидно, не возможна
сокращенная запись уравнения. Этот
случай в дальнейшем не рассматривается.
,
а столбец «обычной» переменной, то это
— регрессия без свободного члена. В
таком случае из (1.18)
не следует (1.19),
и свойства (1.7)
не выполняются. Кроме того, для такой
регрессии, очевидно, не возможна
сокращенная запись уравнения. Этот
случай в дальнейшем не рассматривается.
В дальнейшем будет применяться в основном форма записи уравнения со скры -тым свободным членом, но чтобы не загромождать изложение материала, символ «~» будет опускаться, т.е. соотношения (1.10,1.11,1.12,1.13,1.18) будут исполь¬зоваться в форме
X
= Z + е, (1.21)
+ е, (1.21)
X
= Z +
e, (1.22)
+
e, (1.22)
 =
= m,
(1.23)
m,
(1.23)
 =
(Z'Z)
=
(Z'Z) Z'X, (1.24)
Z'X, (1.24)
Z' =0. (1.25)
=0. (1.25)
Случаи,
когда
 ,
Z, m, M означают не
,
Z, m, M означают не
 ,
,
 ,
, ,
, ,
а собственно
,
а собственно ,
Z, m, M, будут оговариваться специально.
,
Z, m, M, будут оговариваться специально.
1.2. Основные гипотезы, свойства оценок
Применение основной модели линейной регрессии корректно, если выполняются следующие гипотезы:
gl. Между переменными x и z существует линейная зависимость, и (1.10) является истинной моделью, т.е., в частности, правильно определен набор факторов z — модель верно специфицирована.
g2. Переменные z детерминированы, наблюдаются без ошибок и линейно независимы.
g3. Е(е) = 0.
g4. E (ее') = a2IN.
Гипотеза
g2 является слишком жесткой и в экономике
чаще всего нарушается. Возможности
ослабления этого требования рассматриваются
в следующей главе. Здесь можно заметить
следующее: в тех разделах математической
статистики, в которых рассматривается
более общий случай, и z также случайны,
предполагается, что
 не
зависит от этих переменных- регрессоров.
не
зависит от этих переменных- регрессоров.
В
этих предположениях
 относится
к классу
линейных
оценок, поскольку
относится
к классу
линейных
оценок, поскольку
 =
LX, (1.26)
=
LX, (1.26)
где
L (Z'Z)
(Z'Z) Z'
— детерминированная матрица размерности
(n + 1)
Z'
— детерминированная матрица размерности
(n + 1) N, и доказывается ряд утверждений о
свойствах этих
МНК-оценок.
N, и доказывается ряд утверждений о
свойствах этих
МНК-оценок.
1)
 — несмещенная оценка
— несмещенная оценка
 .
.
Действительно:
 (1.27)
(1.27)
и

2)
Ее матрица ковариации
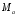 удовлетворяет
следующему соотношению:
удовлетворяет
следующему соотношению:
 =
= (1.28)
(1.28)
в частности,
 1,…,n+1
1,…,n+1

где
m —
j-й диагональный элемент матрицы
—
j-й диагональный элемент матрицы
 .
Действительно:
.
Действительно:

Этот
результат при n = 1 означает, что
 и его можно получить, используя формулу
распространения ошибок первичных
измерений.
и его можно получить, используя формулу
распространения ошибок первичных
измерений.
Действительно,
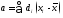 ,
где
,
где .
Тогда
.
Тогда

и в соответствии с указанной формулой:

Здесь важно отметить следующее.
Данная
формула верна и в случае использования
исходной или сокращенной записи уравнения
регрессии, когда M — матрица ковариации
регрессоров. Это следует из (1.17). Но в
такой ситуации она (эта формула) определяет
матрицу ковариации только оценок
коэффициентов регрессии при объясняющих
переменных, а дисперсию оценки свободного
члена можно определить по формуле
 ,
как это следует также из (1.17).
,
как это следует также из (1.17).
Следует также обратить внимание на то, что несмещенность оценок при учете только что полученной зависимости их дисперсий от N свидетельствует о состоятельности этих оценок.
Иногда формулу (1.28) используют в другой форме:
 (1.29)
(1.29)
3)
Несмещенной оценкой остаточной дисперсии
 является
является
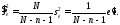 (1.30)
(1.30)
Для
доказательства этого факта сначала
устанавливается зависимость МНК-оценок
ошибок от их истинных значений: (1.31)
(1.31)
и устанавливаются свойства матрицы B
B
= .
(1.32)
.
(1.32)
Эта матрица:
а)вещественна и симметрична: B' = B,
б)вырождена
и имеет ранг N - n - 1, т.к. при любом
 =
0 выполняется BZ
=
0 выполняется BZ = 0
= 0
(поскольку
BZ 0),
а в множестве Z
0),
а в множестве Z в соответствии с g2 имеется точно n +1
линейно независимых векторов,
в соответствии с g2 имеется точно n +1
линейно независимых векторов,
в) идемпотентна:
B = B,
= B,
г) положительно полуопределена в силу симметричности и идемпотентности:
 'B
'B =
= 'B
'B
 =
=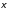 'B'B
'B'B >
0.
>
0.
Теперь
исследуется зависимость остаточной
дисперсии от :
:


где
tr( )
— операция следа матрицы, результатом
которой является сумма ее диагональных
элементов.
)
— операция следа матрицы, результатом
которой является сумма ее диагональных
элементов.
Далее, в силу коммутативности операции следа матрицы
tr
(B) = tr (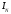 )
- tr (ZL)= N –
)
- tr (ZL)= N – = N - n - 1.
= N - n - 1.
(См. Приложение A. 1.2.)
Таким
образом, E ( )
=
)
= ,
и Е
,
и Е
Что и требовалось доказать.
Тогда
оценкой матрицы ковариации
 является
(в разных вариантах расчета)
является
(в разных вариантах расчета)
 ,
(1.34)
,
(1.34)
и, соответственно, несмещенными оценкамидисперсий (квадратов ошибок) оценок параметров регрессии:

 (1.35)
(1.35)
4)
Дисперсии
 являются наименьшими в классе линейных
несмещенных оценок, т.е. оценки
являются наименьшими в классе линейных
несмещенных оценок, т.е. оценки относятся к классунаилучшей
(с минимальной дисперсией) оценки в
классе несмещенных линейных оценок.
Это утверждение называется теоремой
Гаусса—Маркова.
относятся к классунаилучшей
(с минимальной дисперсией) оценки в
классе несмещенных линейных оценок.
Это утверждение называется теоремой
Гаусса—Маркова.
Доказательство
этого факта будет проведено для оценки
величины
 '
' ,
где
,
где — любой детерминированный вектор-столбец
размерности n +1. Если в качестве
— любой детерминированный вектор-столбец
размерности n +1. Если в качестве выбирать орты, данный факт будет
относиться к отдельным параметрам
регрессии.
выбирать орты, данный факт будет
относиться к отдельным параметрам
регрессии.
МНК-оценка
этой величины есть
 '
'
 c'LX, она линейна, не смещена, т.к. E(
c'LX, она линейна, не смещена, т.к. E( '
' )
=
)
= '
' ,
и ее дисперсия определяется следующим
образом:
,
и ее дисперсия определяется следующим
образом:
var
( '
' )
) .
(1.36)
.
(1.36)
Пусть
d'X — любая линейная оценка
 '
' ,
где d — некоторый детерминированный
вектор- столбец размерности N.
,
где d — некоторый детерминированный
вектор- столбец размерности N.
E
(d'X)
 E
(d'Z
E
(d'Z + d'
+ d' )
) d'Za,
(1.37) и для того, чтобы эта оценка была
несмещенной, т.е. чтобы d'Z
d'Za,
(1.37) и для того, чтобы эта оценка была
несмещенной, т.е. чтобы d'Z = c'
= c' ,
необходимо
,
необходимо
d'Z = c'. (1.38)
Из
(1.37) следует, что d'X = E (d'X) + d' ,
и тогда
,
и тогда
var
(d'X) = E
 =
E (d'
=
E (d'
 'd)
'd) d'd. (1.39)
d'd. (1.39)
И, наконец, в силу положительной полуопределенности матрицы B (из (1.32)):
var
(d'X) - var ( )
) ,
,
т.е. дисперсия МНК-оценки меньше либо равна дисперсии любой другой оценки в классе линейных несмещенных.
Что и требовалось доказать. Теперь вводится еще одна гипотеза:
g5.
Ошибки
 имеют многомерное нормальное распределение:
имеют многомерное нормальное распределение:

 .
.
(Поскольку по предположению g4 они некоррелированы, то по свойству многомерного нормального распределения они независимы).
Тогда
оценки
 будут также иметь нормальное распределение:
будут также иметь нормальное распределение:
 (1.40)
(1.40)
в частности,
![]()
они совпадут с оценками максимального правдоподобия, что гарантирует их состоятельность и эффективность (а не только эффективность в классе линейных несмещенных оценок).
Поскольку
 (1.41)
(1.41)
для
 можно
построить (1 —
можно
построить (1 —
 )100-процентный
доверительный интервал:
)100-процентный
доверительный интервал:
![]() (1.42)
(1.42)
Чтобы
воспользоваться этой формулой, необходимо
знать истинное значение остаточной
дисперсии
 ,
но известна только ее оценка. Для
получения соответcтвующей
формулы в операциональной форме.Сначала
доказывается, что
,
но известна только ее оценка. Для
получения соответcтвующей
формулы в операциональной форме.Сначала
доказывается, что


Теперь матрица B, связывающая в (1.31) оценки ошибок с их истинными значениями, имеет ранг N — n — 1 (см. свойства матрицы B, следующие из (1.32)).
Обращается
внимание на то, что
 и
и не коррелированы, а значит, не коррелированы
случайные величины в (1.41, 1.43).
не коррелированы, а значит, не коррелированы
случайные величины в (1.41, 1.43).
Действительно:
![]()
и
![]()
Что и требовалось доказать.
Поэтому
по определению случайной величины,
имеющей t-распределение:
 (1.44)
(1.44)
Таким
образом, для получения операциональной
формы доверительного интервала в (1.42)
необходимо заменить
 на
на и
и на
на :
:
![]() (1.45)
(1.45)
Приведенные
здесь формулы при n =0 можно считать, что
 =
0 (нулевая гипотеза).
=
0 (нулевая гипотеза).
Рассчитывается t-статистика
![]() (1.46)
(1.46)
которая в рамках нулевой гипотезы, как это следует из (1.44), имеет t-распреде-ление.
Если
уровень значимости t-статистики
 не превышает
не превышает (обычно 0.05), то нулевая гипотеза отвергается
с ошибкой
(обычно 0.05), то нулевая гипотеза отвергается
с ошибкой и принимается, что
и принимается, что .
В противном случае, если нулевую гипотезу
не удалось отвергнуть, считается, что
j-й фактор не значим, и его не следует
вводить в модель.
.
В противном случае, если нулевую гипотезу
не удалось отвергнуть, считается, что
j-й фактор не значим, и его не следует
вводить в модель.
Операции построения доверительного интервала и проверки нулевой гипотезы в данном случае в определенном смысле эквивалентны. Так, если построенный доверительный интервал содержит нуль, то нулевая гипотеза не отвергается, и наоборот.
Гипотеза
о нормальности ошибок позволяет проверить
еще один тип нулевой гипотезы: =
0, j = 1, ..., n, т.е. гипотезы о том, что модель
некорректна и все факторы введены в нее
ошибочно.
=
0, j = 1, ..., n, т.е. гипотезы о том, что модель
некорректна и все факторы введены в нее
ошибочно.
При построении критерия проверки данной гипотезы уравнение регрессии используется в сокращенной форме, и условие (1.40) записывается в следующей форме:

где
 и
и —
вектора коэффициентов при факторных
переменных размерности n, M — матрица
ковариации факторных переменных. Тогда
—
вектора коэффициентов при факторных
переменных размерности n, M — матрица
ковариации факторных переменных. Тогда
![]()
Действительно:
Матрица
 вслед за M является вещественной,
симметричной и положительно
полуопределенной, поэтому ее всегда
можно представить в виде:
вслед за M является вещественной,
симметричной и положительно
полуопределенной, поэтому ее всегда
можно представить в виде:
![]()
где C — квадратная неособенная матрица.
Чтобы
убедиться в этом, достаточно записать
соотношения:
![]() ,
,
где
Y — матрица, столбцы которой есть
собственные вектора
 ,
, —
диагональная матрица соответствующих
собственных чисел. Тогда
—
диагональная матрица соответствующих
собственных чисел. Тогда

(см. Приложение A. 1.2).
Вектор
случайных величин
![]() обладает
следующими свойствами:
обладает
следующими свойствами:
по построению E(u) = 0, ив силу того, что
![]()
![]() Следовательно,
по определению
Следовательно,
по определению
![]() случайная величина
случайная величина

имеет указанное распределение (см. Приложение A.3.2).
Как
было показано выше,
![]() не
коррелированы, поэтому не коррелированы
случайные величины, определенные в
(1.43,1.48), и в соответствии с определением
случайной величины, имеющей F-распределение:
не
коррелированы, поэтому не коррелированы
случайные величины, определенные в
(1.43,1.48), и в соответствии с определением
случайной величины, имеющей F-распределение:
![]()
Отсюда
следует, что при нулевой гипотезе
![]()

или
![]()
Сама
проверка нулевой гипотезы проводится
по обычной схеме. Так, если значение
вероятности
![]() статистики
статистики![]() (величина, аналогичная
(величина, аналогичная![]() для t-статистики) не превышает
для t-статистики) не превышает![]() (например, 0.05), нулевая гипотеза отвергается
с вероятностью ошибки
(например, 0.05), нулевая гипотеза отвергается
с вероятностью ошибки![]() ,
и модель считается корректной. В противном
случае нулевая гипотеза не отвергается,
и модель следует пересмотреть.
,
и модель считается корректной. В противном
случае нулевая гипотеза не отвергается,
и модель следует пересмотреть.
1.3. Независимые факторы: спецификация модели
В этом пункте используется модель линейной регрессии в сокращенной форме, поэтому переменные берутся в центрированной форме, a m и М — вектор и матрица соответствующих коэффициентов ковариации переменных.
Под спецификацией модели в данном случае понимается процесс и результат определения набора независимых факторов. При построении эконометрической модели этот набор должен обосновываться экономической теорией. Но это удается не во всех случаях. Во-первых, не все факторы, важные с теоретической точки зрения, удается количественно выразить. Во-вторых, эмпирический анализ часто предшествует попыткам построения теоретической модели, и этот набор просто неизвестен. Потому важную роль играют и методы формального отбора факторов, также рассматриваемые в этом пункте.
В
соответствии с гипотезой g2 факторные
переменные не должны быть ли¬нейно
зависимыми. Иначе матрица М в операторе
МНК-оценивания будет необратима. Тогда
оценки МНКпо формуле
![]() невозможно будет рассчитать, но их можно
найти, решая систему нормальных уравнений
:
невозможно будет рассчитать, но их можно
найти, решая систему нормальных уравнений
:
![]()
Решений такой системы нормальных уравнений (в случае необратимости матрицы М) будет бесконечно много. Следовательно, оценки нельзя найти однозначно, т.е. уравнение регрессии невозможно идентифицировать. Дйствительноо, уутьь оценено уравнение
![]() (1.51)
(1.51)
где
![]() — вектор-строка факторных переменных
размерности
— вектор-строка факторных переменных
размерности![]() — вектор-столбец соответствующих
коэффициентов регрессии, и пусть в это
уравнение вводится дополнительный
фактор
— вектор-столбец соответствующих
коэффициентов регрессии, и пусть в это
уравнение вводится дополнительный
фактор
![]() ,
линейно зависимый от
,
линейно зависимый от![]() ,
т.е.
,
т.е.![]() Тогда оценка нового уравнения
Тогда оценка нового уравнения
![]() (1.52)
(1.52)
(«звездочкой»
помечены новые оценки «старых» величин)
эквивалентна оценке уравнения
![]() Очевидно,
что
Очевидно,
что![]() и,
произвольно задавая
и,
произвольно задавая![]() ,
можно получать множество новых оценок
,
можно получать множество новых оценок![]() Логичнее всего положить
Логичнее всего положить
![]() ,
т.е. не вводить фактор
,
т.е. не вводить фактор
![]() .
Хотя, если из со-держательных соображений
этот фактор следует все-таки ввести, то
тогда надо исключить из уравнения
какой-либо ранее введенный фактор,
входящий в
.
Хотя, если из со-держательных соображений
этот фактор следует все-таки ввести, то
тогда надо исключить из уравнения
какой-либо ранее введенный фактор,
входящий в![]() .
Таким образом, вводить в модель факторы,
линейно зависимые от уже введенных,
бессмысленно.
.
Таким образом, вводить в модель факторы,
линейно зависимые от уже введенных,
бессмысленно.
 Случаи,
когда на факторных переменных существуют
точные линейные зависимости, встречаются
редко. Гораздо более распространена
ситуация, в которой зависимости между
факторными переменными приближаются
к линейным. Такая ситуация называется
мультиколлинеарностью. Она чревата
высокими ошибками получаемых оценок и
высокой чувствительностью результатов
оценивания к ошибкам в факторных
переменных, которые, несмотря на гипотезу
g2, обычно присутствуют в эмпирическом
анализе.
Случаи,
когда на факторных переменных существуют
точные линейные зависимости, встречаются
редко. Гораздо более распространена
ситуация, в которой зависимости между
факторными переменными приближаются
к линейным. Такая ситуация называется
мультиколлинеарностью. Она чревата
высокими ошибками получаемых оценок и
высокой чувствительностью результатов
оценивания к ошибкам в факторных
переменных, которые, несмотря на гипотезу
g2, обычно присутствуют в эмпирическом
анализе.
Действительно,
в такой ситуации матрица М плохо
обусловлена и диагональные элементы
![]() ,
определяющие дисперсии оценок, могут
принимать очень большие значения. Кроме
того, даже небольшие изменения в М,
связанные с ошибками в факторных
переменных, могут повлечь существенные
изменения в
,
определяющие дисперсии оценок, могут
принимать очень большие значения. Кроме
того, даже небольшие изменения в М,
связанные с ошибками в факторных
переменных, могут повлечь существенные
изменения в![]() и,
как следствие, — в оценках
a.
и,
как следствие, — в оценках
a.
Последнеенаглядноиллюстрируетсярисунком (рис.1.1)впространственаблюдений при n = 2.
На
этом рисунке:
![]()
Видно, чтофакторные переменные сильно коррелированы(угол между соответствующими векторами мал).
Поэтому даже небольшие колебания этих векторов, связанные с ошибками, значительно меняют положение плоскости, которую они определяют, и, соответственно, — нормали на эту плоскость.
Изрисункавидно,что оценки параметров регрессии «слегкостью» меняют не только свою величину, но и знак.
По этим причинам стараются избегать ситуации мультиколлинеарности. Для этого в уравнение регрессии не включают факторы, сильно коррелированные с другими.
Можно попытаться определить такие факторы, анализируя матрицу коэффициентов корреляции факторных переменных S−1MS−1, где S — диагональная матрица среднеквадратических отклонений. Если коэффициент sjj’ этой матрицы достаточно большой, например, выше 0.75, то один из пары факторов j и j’ не следует вводить в уравнение. Однако такого элементарного «парного» анализа может оказаться не достаточно. Надежнее построить все регрессии на множестве факторных переменных, последовательно оставляя в левой части уравнения эти переменные по отдельности. И не вводить в уравнение специфицируемой модели (с x в левой части) те факторы, уравнения регрессии для которых достаточно значимы по F-критерию (например, значение pv не превышает 0.05).
Однако в эмпирических исследованиях могут возникать ситуации, когда только введение сильно коррелированных факторов может привести к построению значимой модели.
Это утверждение можно проиллюстрировать рисунком (рис.1.2) в
пространственаблюдений при n = 2.

Рис. 1.2
На
этом рисунке:
![]()
![]() ,
AD
—
нормаль на
,
AD
—
нормаль на
плоскость, определяемую векторами OB и OC, OD — проекция OA на эту плоскость.
Из
рисунка видно, что
![]() и
и![]() по
отдельности не объясняют
по
отдельности не объясняют![]()
(углы между соответствующими векторами близки к 90◦), но вместе
они определяют плоскость, угол между которой и вектором OA очень
мал,
т.е. коэффициент детерминации в регрессии
![]() на
на
![]() ,
,![]() близок к
близок к
единице.
Рисунок также показывает, что такая ситуация возможна только если
факторы сильно коррелированы.
В таких случаях особое внимание должно уделяться точности измерения факторов.
Далее
определяются последствия введения в
уравнение дополнительного фактора. Для
этого сравниваются оценки уравнений
(1.51, 1.52) в предположении, что
![]() линейно
независим от
линейно
независим от![]() .
.
В этом анализе доказываются два утверждения.
1) Введение дополнительного фактора не может привести к сокращению коэффициента детерминации, в большинстве случаев он растет (растет объясненная дисперсия). Коэффициент детерминации остается неизменным тогда и только тогда, когда вводимый фактор ортогонален остаткам в исходной регрессии (линейно независим от остатков), т.е. когда
![]() (1.53)
(1.53)
(понятно,
что коэффициент детерминации не меняется
и в случае линейной зависимости
![]() от
от![]() ,
но такой случай исключен сделанным
предположением о линейной независимости
этих факторов; в дальнейшем это напоминание
не делается).
,
но такой случай исключен сделанным
предположением о линейной независимости
этих факторов; в дальнейшем это напоминание
не делается).
Для доказательства этого факта проводятся следующие действия.
Записываются системы нормальных уравнений для оценки регрессий (1.51, 1.52):
m1 = M11a1, (1.54)
 Далее,
с помощью умножения обеих частей
уравнения (1.51), расписанного по
наблюдениям, слева на
Далее,
с помощью умножения обеих частей
уравнения (1.51), расписанного по
наблюдениям, слева на
![]() ,
устанавливается, что
,
устанавливается, что
![]() (1.56)
(1.56)
а
из регрессии
![]() ,
в которой по предположению
,
в которой по предположению![]() ,
находится остаточная дисперсия:
,
находится остаточная дисперсия:
![]() . (1.57)
. (1.57)
Из первой (верхней) части системы уравнений (1.55) определяется:
![]() ,
,
и далее
![]() . (1.58)
. (1.58)
Из
второй (нижней) части системы уравнений
(1.55) определяется: ![]() .
.
Откуда
![]() и,
учитывая (1.56, 1.57),
и,
учитывая (1.56, 1.57),
![]() (1.59)
(1.59)
Наконец, определяется объясненная дисперсия после введения дополнительного фактора:
 ,
,
(1.60)
т.е.
![]() .
.
Что и требовалось доказать.
Это утверждение легко проиллюстрировать рисунком 1.3 в пространстве наблюдений при n1 = 1.
На
этом рисунке: OA
—
![]() ,OB
—
,OB
—
![]() ,OC
—
,OC
—
![]() ,AD
—
нормаль xˆ
на
,AD
—
нормаль xˆ
на
![]() (DA
—
вектор e).
(DA
—
вектор e).
Рисунок
показывает, что если
![]() ортогоналенe,
то нормаль
ортогоналенe,
то нормаль
![]() на плоскость, определяемую
на плоскость, определяемую![]() и
и![]() ,
совпадает сAD,
т.е. угол между этой плоскостью и
,
совпадает сAD,
т.е. угол между этой плоскостью и
![]() совпадает
с углом между
совпадает
с углом между![]() и
и![]() ,
введение в уравнение нового фактора
,
введение в уравнение нового фактора![]() не
меняет коэффициент детерминации.
Понятно также и то, что во всех остальных
случаях (когда
не
меняет коэффициент детерминации.
Понятно также и то, что во всех остальных
случаях (когда![]() не
ортогоналенe)
этот угол уменьшается и коэффициент
детерминации растет.
не
ортогоналенe)
этот угол уменьшается и коэффициент
детерминации растет.
После
введения дополнительного фактора
![]()
в
уравнение максимально коэффициент
детерминации может увеличиться до
единицы. Это произойдет, если
![]() является
линейной комбинацией
является
линейной комбинацией![]() и
и![]() .
.
 Рис.
1.3
Рис.
1.3
Рост коэффициента детерминации с увеличе нием количества факторов — свойство коэффициента детерминации, существенно снижающее его содержательное (статистическое) значение.
Введение дополнительных факторов, даже если
они по существу не влияют на моделируемую переменную, приводит к росту этого коэффициента. И, если таких факторов введено достаточно много, то он начнет приближатьсяк единице. Он обязательно достигнет единицы при n = N − 1. Более приемлем в роли критерия качества коэффициент детерминации, скорректированный на число степеней свободы:
![]()
( 1 − R2 — отношение остаточной дисперсии к объясненной, которые имеют, соответственно, N − n − 1 и N − 1 степеней свободы), этот коэффициент может снизиться после введения дополнительного фактора. Однако наиболее правильно при оценке качества уравнения ориентироваться на показатель pv статистики Fc.
Скорректированный коэффициент детерминации построен так, что он, так
сказать, штрафует за то, что в модели используется слишком большой набор факторов. На этом же принципе построено и большинство других критериев, используемых для выбора модели: на них положительно отражается уменьшение остаточной дис персии s2e(z1) (здесь имеется в виду смещенная оценка дисперсии из регрессии по z1) и отрицательно — количество включенных факторов n1 (без константы). Укажемтолькотринаиболееизвестныхкритерия(изогромногочислапредложенных в литературе):
Критерий Маллоуза:
![]() ,
,
где sˆ2e(z) — несмещенная оценка дисперсии в регрессии с полным набором факторов.
Информационный критерий Акаике:
![]() .
.
Байесовский информационный критерий (критерий Шварца):
![]() .
.
В тех же обозначениях скорректированный коэффициент детерминации имеет вид
![]() ,
,
где s2e(∅) — остаточная дисперсия из регрессии с одной константой.
Регрессиятемлучше,чемнижепоказатель
Cp
(
AIC,
BIC
).Для
![]() используется
противоположное правило — его следует
максимизировать. Вместо
используется
противоположное правило — его следует
максимизировать. Вместо![]() при
неизменном количестве наблюденийN
можно
использовать несмещенную остаточную
дисперсию
при
неизменном количестве наблюденийN
можно
использовать несмещенную остаточную
дисперсию
![]() ,которую
уже следует минимизировать.
,которую
уже следует минимизировать.
В
идеале выбор модели должен происходить
при помощи полного перебора возможных
регрессий. А именно, берутся все возможные
подмножества факторов
![]() ,
для каждого из них оценивается регрессия
и вычисляется критерий, а затем выбирается
наборz1,
дающий наилучшее значение используемого
критерия.
,
для каждого из них оценивается регрессия
и вычисляется критерий, а затем выбирается
наборz1,
дающий наилучшее значение используемого
критерия.
Чем
отличается поведение критериев
![]() ,AIC
,
BIC
при
выборе модели? Прежде всего, они
отличаютсяпо степени жесткости,то
естьпо тому, насколько велик штраф за
большое количество факторов и насколько
более «экономную» модель они имеют
тенденцию предлагать.
,AIC
,
BIC
при
выборе модели? Прежде всего, они
отличаютсяпо степени жесткости,то
естьпо тому, насколько велик штраф за
большое количество факторов и насколько
более «экономную» модель они имеют
тенденцию предлагать.
![]() является
наиболее мягким критерием. КритерииCp
и
AIC
занимаютпромежуточноеположение;
при больших N
они
ведутсебя очень похоже, но Cp
несколько
жестче AIC,
особенно прималых N.
BIC
является
наиболее жестким критерием, причем,
как можно увидеть из приведенной
формулы, в отличие от остальных критериев
его жесткость возрастает с ростом N.
является
наиболее мягким критерием. КритерииCp
и
AIC
занимаютпромежуточноеположение;
при больших N
они
ведутсебя очень похоже, но Cp
несколько
жестче AIC,
особенно прималых N.
BIC
является
наиболее жестким критерием, причем,
как можно увидеть из приведенной
формулы, в отличие от остальных критериев
его жесткость возрастает с ростом N.
Различие в жесткости проистекает из различия в целях. Критерии Cp и AIC направлены на достижение высокой точности прогноза: Cp направлен на минимизацию дисперсии ошибки прогноза (о ней речь пойдет в следующем параграфе), а AIC — на минимизацию расхождения между плотностью распределения по ис тинной модели и по выбранной модели. В основе BIC лежит цель максимизации вероятности выбора истинной модели.
2)
Оценки коэффициентов регрессии при
факторах, ранее введенных в уравнение,
как правило, меняются после введения
дополнительного фактора. Они остаются
прежними в двух и только двух случаях:
а) если неизменным остается коэффициент
детерминации и выполняется условие
(1.53) (в этом случае уравнение в целом
остается прежним, т.к. a2
=
0);
б) если новый фактор ортогонален старым
![]() линейно не зависят друг от друга), т.е.
линейно не зависят друг от друга), т.е.
![]() (1.61)
(1.61)

Рис.1.4
(в
этом случае объясненная дисперсия
равна сумме дисперсий, объясненных
факторами
![]() по
от
дельности).
по
от
дельности).
Действительно,
в соотношении (1.58) M11−1m12
не
может равняться нулю при
![]() ,
т.к.
,
т.к.![]() невырожденная
матрица. Поэтому из данного соотношения
следует, что оценки a1
не
меняются,если a2
=
0 (случай
«а») или/и m12
=
0 (случай«б»).
невырожденная
матрица. Поэтому из данного соотношения
следует, что оценки a1
не
меняются,если a2
=
0 (случай
«а») или/и m12
=
0 (случай«б»).
Случай «а», как это следует из (1.59), возникает, когда выполняется (1.53).
В случае «б» соотношение (1.60) переписывается следующим образом:
![]() ,
,
т.к.
вторая (нижняя) часть системы (1.55)
означает в этом случае, что m22a2
=
m2,т.е.
a2
—
оценка параметра в регрессии
![]() :
:
![]() (1.62)
(1.62)
где
s2q2
—
дисперсия
![]() ,
объясненная только
,
объясненная только![]() .
.
Что и требовалось доказать.
Иллюстрацияслучая
«а» при n1
=
1 достаточно
очевидна и дана выше. Рисунок 1.4
иллюстрирует случай «б». На этом
рисунке: OA
—
![]() ,OB
—
,OB
—
![]() ,OC
—
,OC
—
![]() ,EA
—
e,
нормаль
,EA
—
e,
нормаль
![]() на
на![]() ,FA
—
e2,
нормаль
,FA
—
e2,
нормаль
![]() на
на![]() ,DA
—
e∗,
нормаль xˆ
на
плоскость, определенную
,DA
—
e∗,
нормаль xˆ
на
плоскость, определенную
![]() и
и![]() ,ED
—
нормаль к
,ED
—
нормаль к
![]() ,FD
—
нормаль к
,FD
—
нормаль к
![]() .
.
Понятно (геометрически), что такая ситуация, когда точка E является одновременно началом нормалей EA и ED, а точка F — началом нормалей FA и FD, возможна только в случае, если угол COB равен 90◦.
Но
именно этот случай означает (как это
следует из рисунка) одновременное
выполнение соотношений регрессий
(1.51)(ОЕ+ЕА=ОА)(при
![]() ) ( OE+OF
+DA
=
OA)
и(1.62)( OF
+FA
=
OA),
т.е.что введение новогофактора не меняет
оценку при «старом» факторе, а «новая»
объясненная дисперсия равна сумме
дисперсий, объясненных «старым» и
«новым» факторами по отдельности (сумма
квадратов длин векторов OE
и
OF
равна
квадрату длины вектора OD).
) ( OE+OF
+DA
=
OA)
и(1.62)( OF
+FA
=
OA),
т.е.что введение новогофактора не меняет
оценку при «старом» факторе, а «новая»
объясненная дисперсия равна сумме
дисперсий, объясненных «старым» и
«новым» факторами по отдельности (сумма
квадратов длин векторов OE
и
OF
равна
квадрату длины вектора OD).
На основании сделанных утверждений можно сформулировать такое правило введения новых факторов в уравнение регрессии: вводить в регрессию следует такие факторы, которые имеют высокую корреляцию с остатками по уже введенным факторам и низкую корреляцию с этими уже O введенными факторами. В этом процессе следует пользоваться F-критерием: вводить новые факторы до тех пор, пока уменьшается показатель pv
F-статистики.

Рис. 1.5
В таком процессе добавления новых факторов в регрессионную модель некоторые из ранее введенных факторов могут перестать быть значимыми, и их следует выводить из уравнения.
Эту возможность иллюстрирует рисунок 1.5 в пространстве наблюдений
при n1 = 1.
На
этом рисунке: OA
—
![]() ,OB—
,OB—
![]() ,OC
—
,OC
—
![]() ,AD
—
нормаль
,AD
—
нормаль
![]() на
плоскость, определенную
на
плоскость, определенную![]() и
и![]() .
.
Рисунокпоказывает, чтонормаль AD «легла» на вектор вновь введенного фактора. Следовательно, «старый» фактор входит в «новую» регрессию с нулевым коэффициентом.
Это — крайний случай, когда «старый» фактор автоматически выводится из уравнения. Чаще встречается ситуация, в которой коэффициенты при некоторых «старых» факторах оказываются слишком низкими и статистически незначимыми.
Процесс, в котором оценивается целесообразность введения новых факторов и выведения ранее введенных факторов, называется шаговой регрессией. В развитой форме этот процесс можно организовать следующим образом.
Пусть z — полный набор факторов, потенциально влияющих на x. Рассматривается процесс обращения матрицы ковариации переменных x, z, в начале которого рядом с этой матрицей записывается единичная матрица. С этой парой матриц производятся одновременные линейные преобразования. Известно, что если первую матрицу привести таким образом к единичной, то на месте второй будет получена матрица, обратная к матрице ковариации. Пусть этот процесс не завершен, и только n1 строк первой матрицы, начиная с ее второй строки (т.е. со строки первого фактора), преобразованы в орты; z1 — множество факторов, строки которых преобразованы в орты, z2 — остальные факторы. Это — ситуация на текущем шаге процесса.
В начале процесса пара преобразуемых матриц имеет вид (над матрицами показаны переменные, которые соответствуют их столбцам):
 и
и  ,
,
где

На текущем шаге эти матрицы преобразуются к виду:

Информация, используемая в шаговой регрессии, расположена в 1-й строке первой матрицы: остаточная дисперсия в текущей регрессии (в столбце x), коэффициенты a1 текущей регрессии при переменных z1 (в столбцах z1), коэффициенты ce2 ковариации текущих остатков e с переменными z2, не включенными в текущую регрессию (в столбцах z2).
Для введения очередного фактора в регрессию (шаг вперед) следует его строку в первой матрице преобразовать в орт, для исключения фактора из регрессии (шаг назад) следует преобразовать в орт его строку во второй матрице. Шаг вперед увеличиваетколичествоэлементовввекторе z1 наединицуисокращаетнаединицу количество элементов в векторе z2. Шаг назад приводит к обратным изменениям. Последствия любого из этих шагов можно оценить по F-критерию, рассчитав показатель pv Fc-статистики (информацию для такого расчета дает остаточная дисперсия — первый элемент первой строки первой матрицы ).
На текущем шаге процесса проверяются последствия введения всех ранее не введенных факторов z2 и исключения всех введенных факторов z1. Выбирается тот вариант, который дает минимальное значение показателя pv. Процесс заканчивается, как только этот показатель перестает падать. В результате определяетсянаилучшаярегрессия. Такой процессне приводит,как правило,к включению в регрессию сильно коррелированных факторов, т.е. позволяет решить проблему мультиколлинеарности.
Если бы расчеты проводились в стандартизированной шкале (по коэффициентам корреляции, а не ковариации), «кандидатом» на введение был бы фактор с максимальным значением показателя в множестве ce2 (как было показано выше), а на исключение — фактор с минимальным значением показателя в множестве a1. Но даже в этом случае для окончательного выбора (вводить-исключать) и решения вопроса о завершении процесса требуется использование F-критерия. При «работе» с коэффициентами ковариации использование F-критерия необходимо.
На последних шагах процесса, при приближении к минимуму критериального показателя pv,его величина меняется,как правило, весьма незначительно. Поэтому один из возможных подходов к использованию шаговой регрессии заключается в определении некоторого множества регрессий, получаемых на последних шагах процесса, которые практически одинаковы по своему качеству. И на этом множестве следует делать окончательный выбор, пользуясь содержательными критериями.
Иногда процесс шаговой регрессии предлагают строить на основе t-критерия: фактор вводится в уравнение, если его t-статистика больше некоторой заданной величины t1, выводится из уравнения, если эта статистика меньше заданной величины t2; как правило, t1 > t2. Такой процесс не гарантирует получение наилучшей регрессии, его использовали в то время, когда вычислительные возможности были еще слабо развиты, и, в частности, точные значения показателя pv было трудно определить.
