Время прохождения луча и дисперсия материала
•Для описания уширения импульса необходимо знать время прохождения луча t по разным траекториям. Скорость света вдоль лучевой траектории
• vg = c / nco |
, |
(Ф. - 17) |
•где с – скорость света в вакууме. При этом время прохождения луча из (Ф. – 7-16) определяется, как
• t = |
z |
|
Lp |
|
z |
|
L |
|
z |
|
n2 |
|
z |
|
n |
co |
|
|
||
|
|
|
= |
|
|
o |
= |
|
|
|
co |
= |
|
|
|
, |
(Ф. - 18) |
|||
z p |
|
vg |
z p |
|
c |
c |
|
|
|
|
c |
|
cosθz |
|||||||
|
|
|
β |
|
|
|
||||||||||||||
• следовательно, чем больше θz, тем больше время прохождения луча.
• Показатель преломления зависит от длины волны, т.е. .
nco = nco (λ)
Время прохождения луча и дисперсия материала
•При наличии дисперсии групповая скорость дается выражением
|
|
|
dn |
co |
(λ) −1 |
||
• |
vg |
= c nco (λ)−λ |
|
|
|
||
dλ |
|||||||
|
|
|
|
||||
•Определим групповой показатель преломления, как
•ng = nco (λ)−λ dλ ) ,dnco (λ
(Ф. - 19)
(Ф. - 20)
•Для времени прохождения луча окончательно получим:
• |
t = |
z |
|
ng |
= |
z |
|
ng nco |
(Ф. - 21) |
||
c cosθz |
c |
|
|
|
|
||||||
|
β |
||||||||||
|
|
|
|
|
|||||||
и является функцией θz и λ.
Планарные волноводы с градиентным профилем
•Обобщим результаты предыдущего раздела на распространение лучей в ОВ с градиентной сердцевиной.
Траектории лучей
•Траектория луча в общем случае определяется уравнением эйконала:
|
d |
dr |
|
|
|
||
• |
|
n(r) |
|
|
= n(r) |
, |
(Ф. - 22) |
|
|
||||||
ds |
ds |
|
|||||
• В случае планарного волновода n(x) зависит только от
одной координаты. Из (Ф. - 21) для этого случая имеем:
d |
dx |
|
dn(x) |
|
d |
|
dz |
|
|
||||
|
n(x) |
|
|
= |
|
|
, |
|
n(x) |
|
|
= 0 |
(Ф. - 23) |
|
|
dx |
|
|
|||||||||
ds |
ds |
|
|
ds |
ds |
|
|||||||
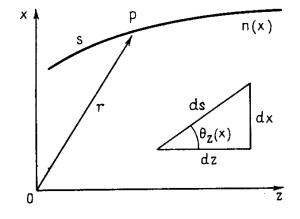
Рис. 6. - Параметры, описывающие расстояние вдоль траектории луча.
Если ввести угол θz, между касательной к траектории луча и осью волновода (см.Рис. 6), то можно записать:
dx |
= sinθz (x); |
dz |
= cosθz (x) |
. (Ф. - 24) |
|
ds |
ds |
||||
|
|
|
Траектории лучей
•Проинтегрировав второе уравнение (Ф. - 23) получим:
• n(x)cosθz (x)= n(0)cosθz (0) |
, |
(Ф. - 25) |
•справедливое при всех x. Оно является обобщением закона
Снелля. Для градиентных сред. При этом n(x)cosθz (x)
постоянно вдоль траектории луча. Для конкретного профиля траектория луча однозначно определяется начальным углом
θz(0).