§ 27. Линия в пространстве и ее уравнения. Линия в пространстве может быть задана двумя уравнениями

F(х,у,z)=0, Ф(х,у,z)=0 (1)

поверхностей, пересекающихся по этой линии. Линию в простран­стве иногда задают параметрически:

x=x(t), y=y(t), z=z(t), (2)

причем параметрические уравнения линии в пространстве опреде­ляются так же, как и параметрические уравнения линии на пло­скости.

Если поверхность S задана параметрически:

x=x(u,), y=y(u,), z=z(u,), (3)

то линию С, лежащую на этой поверхности, часто определяют одним уравнением f(u,)=0 (в частности и=и() или =(u)) между криволинейными координатами и и . Уравнение f(u,)=0, (4) называется уравнением линии С, если любая пара значений и, ,удовлетворяющая уравнению (4), не выходит из общей области определения D функций х(и,), у(и,) и z(и,), а точка М с коор­динатами х(и,), у(и,), z(и,) лежит на линии С. Обратно, для любой точки М линии С найдется "пара чисел и, , входящая в область D и такая, что f (и,)=0, а х(и,), у(и,), z(и,)- координаты точки М.

В частности, линии, выражаемые уравнениями u=C₁, =C₂ , где C₁ и C₂ — постоянные, называются координатными линиями поверхности S, заданной параметрическими уравнениями (3). Вместо одного уравнения (4) линию С на поверхности S задают и пара­метрически (в криволинейных координатах и,):

u=u(t), = (t). (5)

Эти два уравнения называются внутренними уравнениями линии, лежащей на поверхности S, заданной уравнениями (3), если функции u(t) и (t) имеют общую область определения D₁, любому числу t из области D₁ соответствует пара чисел u(t), (t), не выходящих из области D и таких, что точка M[x(u(t), (t)), y(u(t), (t)), z(u(t), (t))] лежит на линии С. Обратно, для любой точки М линии С существует число t, обладающее указанным свойством.

§ 28. Примеры уравнений линий в пространстве.

Пример 1. Уравнения относительно декартовой прямоугольной системы координат выражают окруж­ность С радиуса а с центром в начале координат, лежащую в плоскости хОу, так как первое уравнение, т. е. есть уравнение круглого цилиндра радиуса а, осью которого является Оz, a z=0 есть уравнение плоскости хОу. Эти две поверхности пересекаются по окружности С.

Пример 2. Пусть точка М движется равномерно по окружности радиуса a так, что радиус ОМ этой окружности вращается с постоянной угловой ско­ростью , а плоскость окружности движется равномерно и поступательно в пространстве так, что ее центр перемещается по прямой, перпендикулярной плоскости окружности, с постоянной скоростью . Тогда точка М описывает линию, называемую обыкновенной винтовой линией.

Примем центр окружности в начальном ее положении за начало коорди­нат, плоскость, в которой она расположена - за плоскость хОу, а прямую, проходящую через центр окружности перпендикулярно ее плоскости - за ось Оz (рис. 68) (оси Ох и Оу взаимно перпендикулярны).

Рис. 68 Рис. 69

Пусть М₀(а,0,0) - начальное положение движущейся точки. За время t точка М₀ пройдет по окружности дугу, равную , а в направлении осиОz пройдет путь t,

Следовательно, ее координаты в момент t будут: x=acost, y=asint, z=t.

Произведем замену параметра, полагая где ,

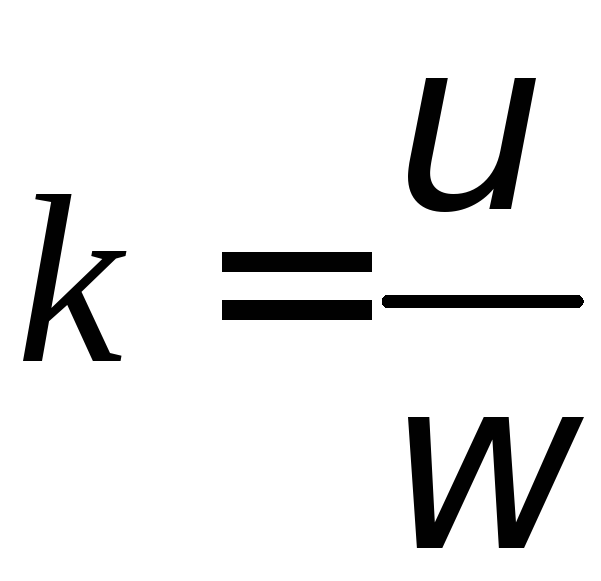получим

x = acos u, y = asin u, z = ku. (1)

Эти уравнения и являются параметрическими уравнениями винтовой линии. Они выражают закон движения точки по этой винтовой линии. Параметр и принимает все, действительные значения. Если заменить на противо­положное направление вращения радиуса (или перемещение плоскости окружности), то получим винтовую линию противоположной нарезки.

Различают правую и левую винтовые ли­нии (рис. 69).

Математически имеет смысл говорить лишь о винтовых линиях противоположных или одинаковых ориентации; понятие о пра­вой и левой винтовых линиях имеет лишь физический смысл.

Пример 3. Рассмотрим параметрические уравнения сферы с центром в начале координат и

радиусом а (система координат декар­това прямоугольная):

,

Координатными линиями u=С, где С - число из полуинтервала [0,2), являются се­чения этой сферы полуплоскостями, проходя­щими через осьОz; это - полумеридианы сферы (если за полюсы принять точ­ки (0,0,±)). Координатными линиями =С, где С—число из интервала , являются сечения сферы плоскостями, перпендикулярными осиОz; это - параллели. Уравнения выполняются соот-ветст­венно только для полюсов , .

П

ример 4. Рассмотрим прямой кру­говой цилиндр радиуса а, ось которого совпадает с осью Oz. Уравнение этого цилиндра можно записать в виде , но можно записать и в параметриче­ской форме:

где

где(D)

где и-угол от оси Ох до луча ОМ', а М'- проекция произвольной точки М(х,у,z), лежащей на поверхности цилиндра, в плоскость хОу.

Линейное однородное уравнение

=ku, где

есть внутреннее уравнение винтовой линии, лежащей на рассматриваемом цилиндре. Параметрические уравнения этой винтовой линии;

x=acosu, y=asinu, z=ku

(см. уравнения (1) примера 2 этого параграфа).

В заключение отметим координатные линии цилиндра, заданного параме­трическими уравнениями (1). Линии и=С-это прямолинейные образующие цилиндра, так как если и имеет постоянное значение из полуинтервала [0,2), то точкаМ(х,у,z) поверхности цилиндра проектируется в фик­сированную точку М'(acosС,asinС,0), и при изменении от - до + точка М(acosС,аsinС,) описывает прямолинейную образующую, проходя­щую через точку М'. Линии =C (где С-любое число) являются окружно­стями, по которым плоскость, перпендикулярная к оси цилиндра, пересекает этот цилиндр.