
Аналитическая геометрия.
Глава 9. Поверхности второго порядка, заданные каноническими уравнениями Лекция 5. § 128. Эллипсоид
Определение.
Эллипсоидом называется поверхность,
уравнение которой в некоторой специально
выбранной прямоугольной системе
координат, имеет вид:
 (1)
(1)
Будем считать,
что
![]() .
Если на эллипсоиде лежит точка
.
Если на эллипсоиде лежит точка![]() ,
то на нём лежат и точки
,
то на нём лежат и точки![]() (с любым набором знаков плюс или минус).
Отсюда следует, что для эллипсоида (1)
начало координат
(с любым набором знаков плюс или минус).
Отсюда следует, что для эллипсоида (1)
начало координат![]() является его центром симметрии и
называется центром эллипсоида; оси
координат являются осями симметрии и
называются главными осями; плоскости
координат являются плоскостями симметрии
и называются главными плоскостями.
является его центром симметрии и
называется центром эллипсоида; оси
координат являются осями симметрии и
называются главными осями; плоскости
координат являются плоскостями симметрии
и называются главными плоскостями.
Если
![]() ,
то эллипсоид называется трёхосным.
,
то эллипсоид называется трёхосным.
Если
![]() ,
то эллипсоид называется вытянутым
эллипсоидом вращения; он получается
вращением эллипса:
,
то эллипсоид называется вытянутым
эллипсоидом вращения; он получается
вращением эллипса: вокруг его большей оси (См. рис. 197)
вокруг его большей оси (См. рис. 197)
Если
![]() ,
то эллипсоид называется сжатым эллипсоидом
вращения; он получается вращением
эллипса:
,
то эллипсоид называется сжатым эллипсоидом
вращения; он получается вращением
эллипса: вокруг его малой оси (См. рис. 198)
вокруг его малой оси (См. рис. 198)

Рис. 198.
Если
![]() ,
тоэллипсоид является сферой радиуса
,
тоэллипсоид является сферой радиуса![]() с центром в начале координат.
с центром в начале координат.
Вершинами
трёхосного эллипсоида являются точки
пересечения эллипсоида с его главными
осями. Трёхосный эллипсоид имеет 6 вершин
![]() ,
,![]() ,
,![]() .
.
Из уравнения (1)
следует, что
![]() ,
,![]() ,
,![]() .
Это означает, что эллипсоид (1) лежит
внутри прямоугольного параллелепипеда
с вершинами
.
Это означает, что эллипсоид (1) лежит
внутри прямоугольного параллелепипеда
с вершинами![]() .
Каждая грань этого параллелепипеда
имеет с эллипсоидом только одну общую
точку - его вершину.
.
Каждая грань этого параллелепипеда
имеет с эллипсоидом только одну общую
точку - его вершину.
Плоскость
![]() пересекает эллипсоид (1) по линии,
выраженной уравнениями:
пересекает эллипсоид (1) по линии,
выраженной уравнениями: ,
,![]() или эквивалентной системой:
или эквивалентной системой: (2)
(2)
Аналогично
плоскость
![]() пересекает эллипсоид (1) по линии,
уравнения которой:
пересекает эллипсоид (1) по линии,
уравнения которой: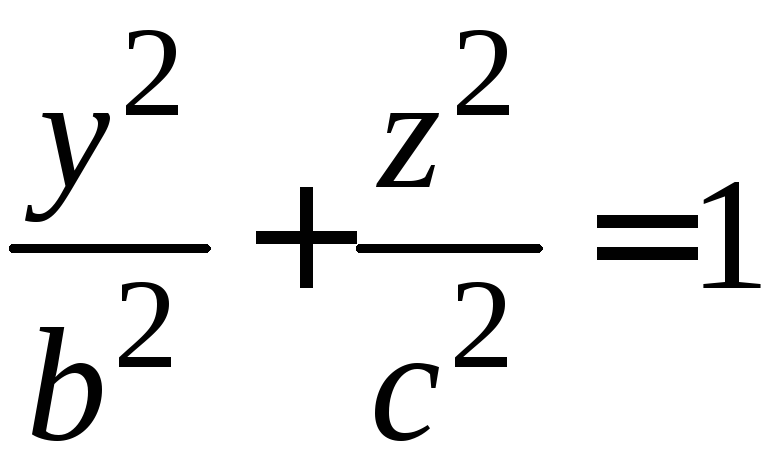 ,
,![]() ,
(3) а плоскость
,
(3) а плоскость![]() по линии:
по линии: ,
,![]() .
(4)
.
(4)
Линии (2), (3), (4) суть эллипсы. Эти эллипсы, т.е. сечения эллипсоида (1) его главными плоскостями, называются главными сечениями.
Рассмотрим сечения
эллипсоида какими-нибудь координатными
плоскостями, например плоскостями,
параллельными плоскости
![]() ,
т.е. плоскостями, выраженными уравнением
,
т.е. плоскостями, выраженными уравнением![]() ,
где
,
где![]() - произвольное действительное число. В
таком случае, уравнения линии сечения
имеют вид:
- произвольное действительное число. В
таком случае, уравнения линии сечения
имеют вид: ,
,![]() ,
или
,
или ,
,![]() ,
или:
,
или: (5) Если
(5) Если![]() ,
то первому уравнению системы (5) не
удовлетворяет ни одна пара действительных
чисел
,
то первому уравнению системы (5) не
удовлетворяет ни одна пара действительных
чисел![]() т.е. система (5) не имеет действительных
решений
т.е. система (5) не имеет действительных
решений![]() .
это означает, что плоскость
.
это означает, что плоскость![]() при
при![]() не пересекает эллипсоид (1).
не пересекает эллипсоид (1).
При
![]() первое уравнение системы (5) имеет вид:
первое уравнение системы (5) имеет вид: ,
откуда
,
откуда![]() .
Таким образом, плоскости
.
Таким образом, плоскости![]() встречают эллипсоид (1) в его вершинах
встречают эллипсоид (1) в его вершинах![]() .
Наконец, если
.
Наконец, если![]() ,
то систему уравнений (5), выражающих
линию сечения, можно переписать так:
,
то систему уравнений (5), выражающих
линию сечения, можно переписать так: ,
,![]() .
.
Или:
 ,
,![]() .
.
Эти уравнения
являются уравнения эллипса, лежащего
в плоскости сечения
![]() ;
центр этого эллипса - точка
;
центр этого эллипса - точка![]() ,
оси симметрии параллельны осям
,
оси симметрии параллельны осям![]() и
и![]() ,
а полуоси равны:
,
а полуоси равны: ,
, .
Таким образом, любое сечение эллипсоида
плоскостями, параллельными координатным,
дают в сечении эллипс.
.
Таким образом, любое сечение эллипсоида
плоскостями, параллельными координатным,
дают в сечении эллипс.
Отметим, что
эллипсоид (1) может быть получен из сферы
![]() ,
если провести 3 равномерных сжатия:
,
если провести 3 равномерных сжатия:![]() ;
;![]() ;
;![]() к трём попарно перпендикулярным
плоскостям.
к трём попарно перпендикулярным
плоскостям.
§ 129. Однополостный гиперболоид
Определение.
Однополостным гиперболоидом на-зывается
поверхность, уравнение которой в
некоторой специально выбранной
прямоугольной системе коор-динат, имеет
вид:
 (6)
(6)
Будем считать,
что
![]() .
Также как и в преды-дущем параграфе
доказывается, что для однополостного
гиперболоида (6) начало координат является
центром симметрии (центр однополостного
гиперболоида). Оси координат являются
осями симметрии (главные оси), а
координатные плоскости - плоскостями
симметрии (главные плоскости) (См. рис.
200).
.
Также как и в преды-дущем параграфе
доказывается, что для однополостного
гиперболоида (6) начало координат является
центром симметрии (центр однополостного
гиперболоида). Оси координат являются
осями симметрии (главные оси), а
координатные плоскости - плоскостями
симметрии (главные плоскости) (См. рис.
200).

Рис. 200.
Если в уравнении
(6)
![]() ,
то однополостный гиперболоид (6) называется
однополостным гиперболоидом вращения,
так как может быть получен вращением
гиперболы
,
то однополостный гиперболоид (6) называется
однополостным гиперболоидом вращения,
так как может быть получен вращением
гиперболы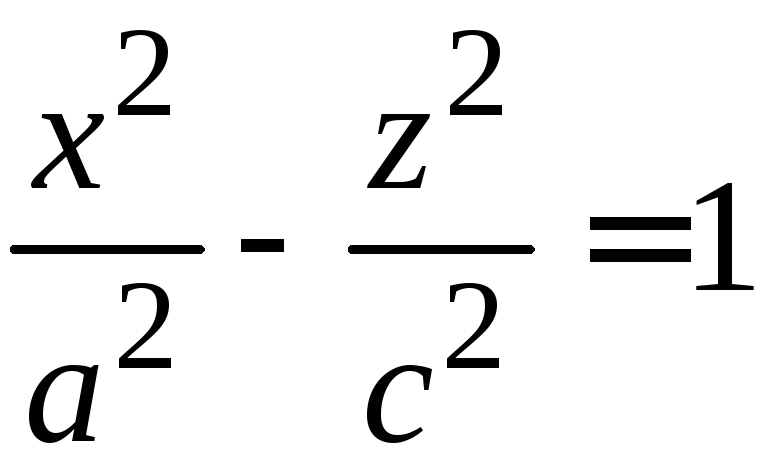 вокруг мнимой оси (См. рис. 200).
вокруг мнимой оси (См. рис. 200).
Вершинами
однополостного гиперболоида называ-ются
точки пересечения гиперболоида с его
главными осями. Гиперболоид (6) в случае
![]() имеет 4 вершины
имеет 4 вершины![]() ;
;![]() .
.
Плоскость
![]() пересекает однополостный гипер-болоид
(6) по эллипсу, выраженному уравнениями:
пересекает однополостный гипер-болоид
(6) по эллипсу, выраженному уравнениями:
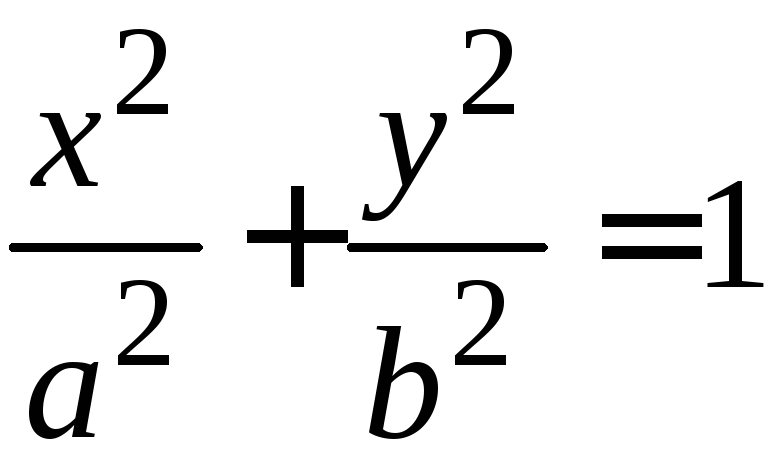 ,
,
![]() ,
называемому горловым эллипсом
однополостного гиперболоида (6). Плоскость
,
называемому горловым эллипсом
однополостного гиперболоида (6). Плоскость![]() пересекает однополостный гиперболоид
(6) по гипер-боле, выраженной уравнениями:
пересекает однополостный гиперболоид
(6) по гипер-боле, выраженной уравнениями: ,
,![]() .
.
А плоскость
![]() пересекает однополостный гиперболоид
(6) по гиперболе, выраженной уравнениями:
пересекает однополостный гиперболоид
(6) по гиперболе, выраженной уравнениями: ,
,![]() .
.
Рассмотрим сечения
однополостного гиперболоида (6)
плоскостями, параллельными координатной
плоскости
![]() ,
т.е. плоскостями
,
т.е. плоскостями![]() .
Уравнения линии сечения будут:
.
Уравнения линии сечения будут: ;
;![]() .
Эта система уравнений эквивалентна
следующей системе:
.
Эта система уравнений эквивалентна
следующей системе: ;
;![]() или
или
 ;
;
![]() .
.
Этими уравнениям
выражается эллипс с полуосями
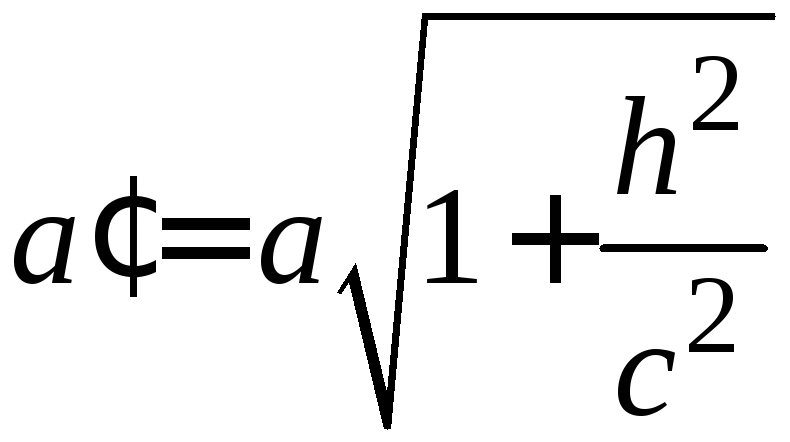 ,
, с центром на оси
с центром на оси![]() в точке
в точке![]() и осями, параллельными соответственно
осям
и осями, параллельными соответственно
осям![]() и
и![]() .
из выражений
.
из выражений ,
, следует, что
следует, что![]() ,
,![]() ,
т.е. горловой эллипс является наименьшим
из всех эллипсов, по которым однополостный
гиперболоид (6) рассекается плоскостями,
параллельными плоскости
,
т.е. горловой эллипс является наименьшим
из всех эллипсов, по которым однополостный
гиперболоид (6) рассекается плоскостями,
параллельными плоскости![]() .
.
Плоскость
![]() ,
параллельная плоскости
,
параллельная плоскости![]() ,
пересекает однополостный гиперболоид
(6) по линии, выражаемой уравнениями:
,
пересекает однополостный гиперболоид
(6) по линии, выражаемой уравнениями: ;
;![]() .
Или
.
Или ;
;![]() .
.
Если
![]() ,
то этими уравнениями определяется
гипербола с центром в точке
,
то этими уравнениями определяется
гипербола с центром в точке![]() ,
лежащая в плоскости
,
лежащая в плоскости![]() ,
действительная ось которой параллельна
оси
,
действительная ось которой параллельна
оси![]() ,
а мнимая - оси
,
а мнимая - оси![]() .
Полуоси этой гиперболы:
.
Полуоси этой гиперболы: (действительная полуось),
(действительная полуось), - (мнимая полуось).
- (мнимая полуось).
Если
![]() ,
то уравнения линии сечения имеет
,
то уравнения линии сечения имеет
вид:
 ;
;![]() .
Уравнения
.
Уравнения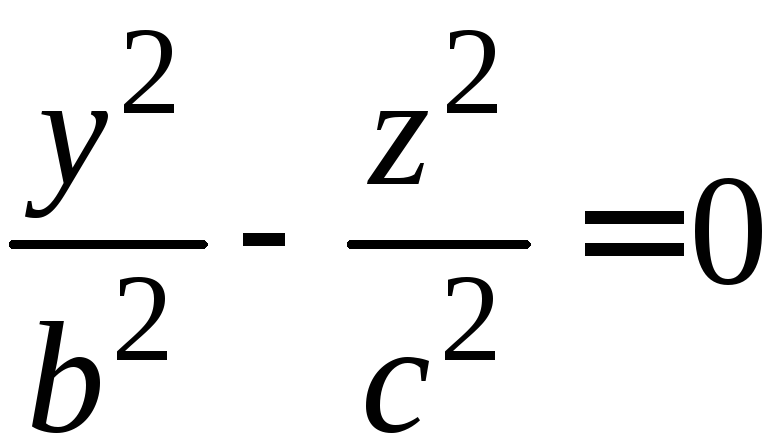 ;
;![]() являются уравнениями двух пересекающихся
прямых
являются уравнениями двух пересекающихся
прямых![]() и
и![]() :
: ,
,![]() - прямая
- прямая![]() ;
; ,
,![]() - прямая
- прямая![]() .
.
Аналогично
уравнения
 ;
;![]() являются уравнениями двух пересекающихся
прямых:
являются уравнениями двух пересекающихся
прямых: ,
,![]() и
и ,
,![]() .
.
Если
![]() ,
то в сечении получается гипербола,
уравнения которой:
,
то в сечении получается гипербола,
уравнения которой: ;
;![]() .
.
Действительная
ось этой гиперболы параллельна оси
![]() ,
мнимая - оси
,
мнимая - оси![]() ,
центр лежит в точке
,
центр лежит в точке![]() .
.
Асимптоты всех
гипербол, получающихся при пересечении
однополостного гиперболоида (6) плоскостями
![]() ,
,![]() параллельны прямым, получающимся при
пересечении гиперболоида плоскостями
параллельны прямым, получающимся при
пересечении гиперболоида плоскостями![]() .
.
Сечения плоскостями
![]() ,
параллельными плоскости
,
параллельными плоскости![]() аналогичны рассматриваемым. Все эти
сечения дают представление о форме
поверхности однополостного гиперболоида
(См. рис. 201).
аналогичны рассматриваемым. Все эти
сечения дают представление о форме
поверхности однополостного гиперболоида
(См. рис. 201).

Рис. 201.
Всякий однополостный
гиперболоид можно получить из
однополостного гиперболоида вращения:
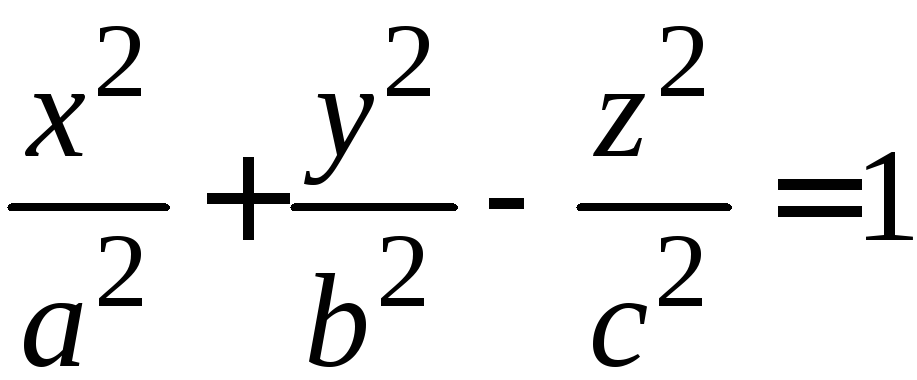 ,
,![]() производя равномерное сжатие
производя равномерное сжатие .
.![]() ,
,![]() к плоскости
к плоскости![]() . Однополостный
гиперболоид (6) можно получить из
равностороннего гиперболоида вращения:
. Однополостный
гиперболоид (6) можно получить из
равностороннего гиперболоида вращения:
![]() ,
производя равномерные сжатия
,
производя равномерные сжатия
![]() ,
,![]() ,
,![]() соответственно к плоскостям
соответственно к плоскостям![]() ,
,![]() и
и![]() с коэффициентами сжатия
с коэффициентами сжатия![]() .
.
