Аналитическая геометрия.

Глава 11. Линии второго порядка, заданные общими уравнениями

Лекция 9. § 144. Центр линии второго порядка

Определение. Центром линии второго порядка называется центр симметрии этой линии, т.е. точка , обладающая следующим свойством: если на линии лежит точка (действительная или мнимая), то на этой же линии лежит точка, симметричная точкеотносительно.

Теорема 1. Пусть относительно ОДСК задана линия второго порядка общим уравнением:

Для того, чтобы начало координат являлось её центром, необходимо и достаточно, чтобы в уравне-нии (1) отсутствовали члены с ив первой степени, т.е., чтобы. Иначе, чтобы уравнение линии имело вид: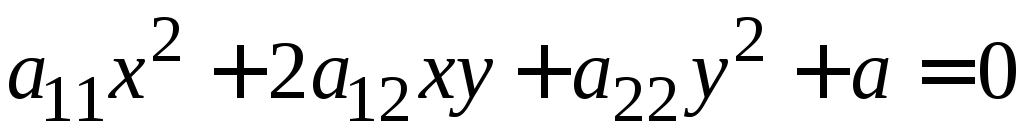. (2)

Доказательство достаточности. Если , то уравнение линии имеет вид (2), и, если ему удовлет-воряют координатыиточки, то ему удовлетво-ряют и координатыиточки, симметричнойотносительно начала координат.

Доказательство необходимости. Пусть начало ко-ординат является центром линии (1). Предположим вопреки утверждению теоремы, что по крайней мере одно из чисел илиотлично от нуля. Возьмём на линии (1) произвольную точку. Её координа-ты удовлетворяют уравнению (1), а так как начало координат является центром симметрии линии (1), то уравнению (1) удовлетворяют и координаты точкисимметричной точкеотноситель-но начала координат, то есть

Из этого соотношения и из соотношения (1) находим:

, то есть . ЧТД.

Теорема 2. Если относительно ОДСК линия второ-го порядка задана общим уравнением (1), то координаты ,её центра определяются из системы уравнений:(2)

причём в случае несовместности этой системы, линия не имеет центра (т.е. является параболой).

Доказательство. Произведём перенос Декартовой системы так, чтобы новым началом координат стала точка . Обозначая координаты про-извольной точкив новой системечерез,, будем иметь:;, и уравнение (1) примет вид

На основании предыдущей теоремы 1 точка является центром данной линии тогда и только тогда, когда, когда: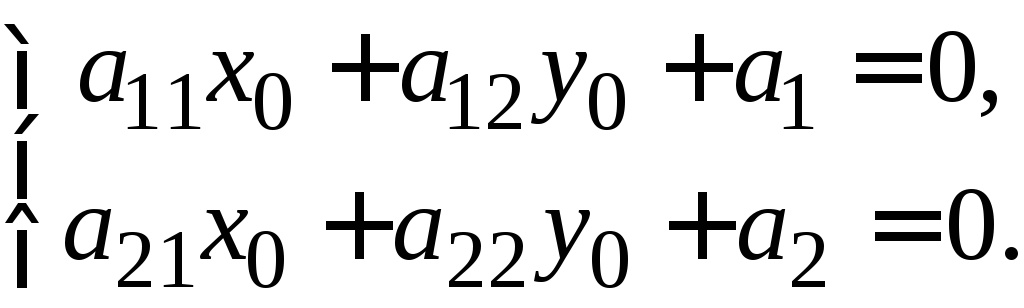

Теперь, если , то система (2) имеет единственное решение, т.е. линия (1) имеет единственный центр. Если система (2) несовместна, то линия не имеет центра, т.е. является параболой. Если система (2) неопределённая, т.е. имеет бесчисленное множество решений, то линия (1) имеет бесконечное множество центров - прямую центров, так как в случае неопределённости системы множество всех её реше-ний есть множество всех решений уравнения первой степени относительнои.

Данная ранее классификация линий второго порядка по группам I, II, III, является классификацией этих линий по характеру их места центров: линии группы I имеют единственный центр (начало координат в их простейшем уравнении); линии группы II не имеют центра (парабола); линии группы III имеют прямую центров (ось в простейшем уравнении). В этом можно убедиться, составляя систему уравнений (3) для определения центра для каждого из уравнений:

I. 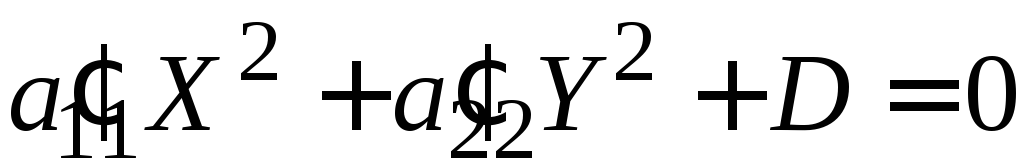,,. Здесь, система (3) равна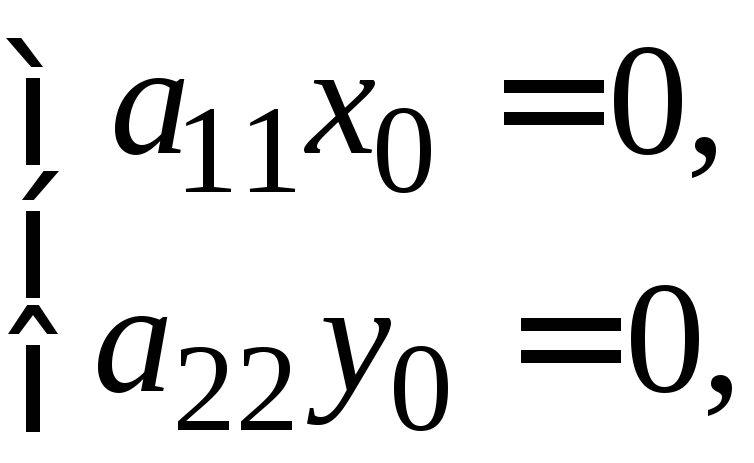то есть центром является начало координат.

II. 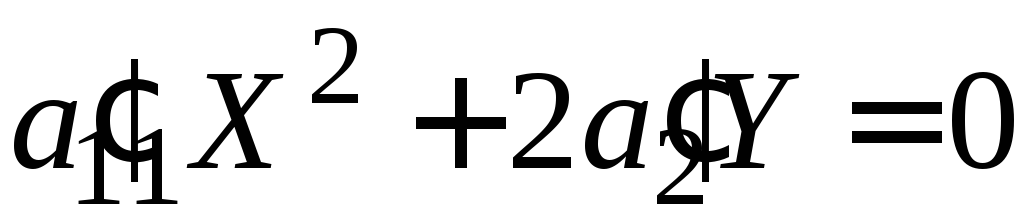,,. Здесь, система (3) равнато есть решения нет и, значит, линия не имеет центра.

III. ,. Здесь, система (3) равнато есть, а это ось , значит, здесь целая прямая центров.