
Лекции по геометрии - Лекция 6 для М-А
.docАналитическая геометрия.
Глава 9. Поверхности второго порядка, заданные каноническими уравнениями
Лекция 6. § 133. Эллиптический параболоид
Определение.
Эллиптическим параболоидом назы-вается
поверхность, уравнение которой в
некоторой специально выбранной
прямоугольной системе коор-динат, имеет
вид:
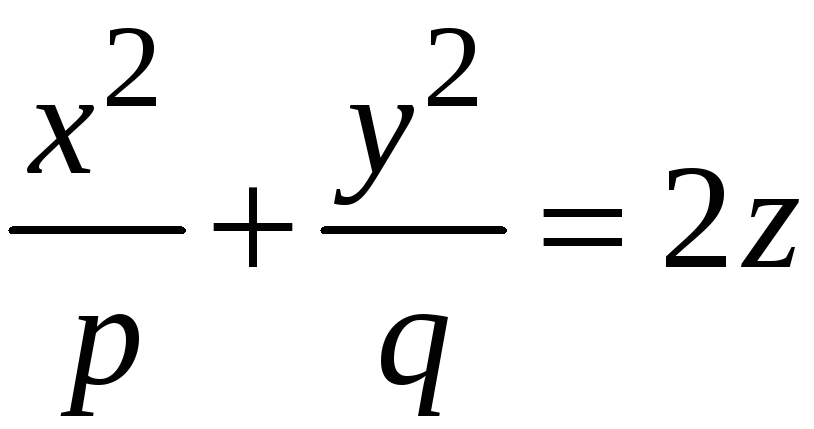 ,
(1)
,
(1)
где
![]() ,
,
![]() .
Будем считать, что
.
Будем считать, что
![]() .
Если
.
Если
![]() ,
то эллиптический параболоид (1) является
параболоидом вращения, т.к. получается
вращением параболы:
,
то эллиптический параболоид (1) является
параболоидом вращения, т.к. получается
вращением параболы:
![]() вокруг оси
вокруг оси
![]() ,
являющейся осью параболы.
,
являющейся осью параболы.
Ось
![]() является осью симметрии эллиптического
параболоида (1) (она называется осью
параболида), а плоскости
является осью симметрии эллиптического
параболоида (1) (она называется осью
параболида), а плоскости
![]() и
и
![]() - плоскостями симметрии (главные
плоскости). Начало координат для
эллиптического параболоида (1) является
точкой пересечения этой поверхности с
её осью и называется вершиной.
- плоскостями симметрии (главные
плоскости). Начало координат для
эллиптического параболоида (1) является
точкой пересечения этой поверхности с
её осью и называется вершиной.
Плоскость
![]() пересекает эллиптический парабо-лоид
(1) по линии:
пересекает эллиптический парабо-лоид
(1) по линии:
 ,
,
![]() ;
или
;
или
 ,
,
![]() ;
(2)
;
(2)
Если
![]() ,
то первое уравнение не имеет действительных
решений, т.к.
,
то первое уравнение не имеет действительных
решений, т.к.
![]() ,
,
![]() ,
это означает, что плоскость
,
это означает, что плоскость
![]() при
при
![]() не пересекает эллиптический параболоид
(1),
не пересекает эллиптический параболоид
(1),
Если
![]() ,
то
,
то
![]() ,
т.е. плоскость
,
т.е. плоскость
![]() имеет с эллиптическим параболоидом
только одну общую точку - вершину
имеет с эллиптическим параболоидом
только одну общую точку - вершину
![]() .
.
Если
![]() ,
то переписав уравнение (2) в виде:
,
то переписав уравнение (2) в виде:
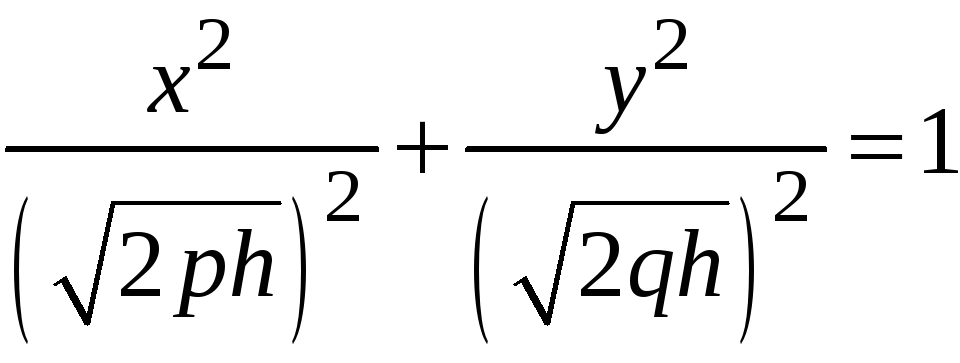 ,
,
![]() ,
видим, что сечением является эллипс с
центром в точке
,
видим, что сечением является эллипс с
центром в точке
![]() и полуосями:
и полуосями:
![]() и
и
![]() .
.
Плоскость
![]() пересекает эллиптический параболоид
(1) по параболе
пересекает эллиптический параболоид
(1) по параболе
![]() ,
,
![]() ,
а плоскость
,
а плоскость
![]() по параболе
по параболе
![]() ,
,
![]() .
.
Таким образом,
числа
![]() и
и
![]() - параметры парабол, получающихся в
сечении параболоида плоскостями
симметрии (См. рис. 207).
- параметры парабол, получающихся в
сечении параболоида плоскостями
симметрии (См. рис. 207).

Рис. 207. Рис. 208.
Рассмотрим сечения
эллиптического параболоида плоскостями,
параллельными плоскостям
![]() ,
т.е. плоскостями, выражаемыми уравнением
,
т.е. плоскостями, выражаемыми уравнением
![]() .
.
Уравнение линии сечения будет следующим:
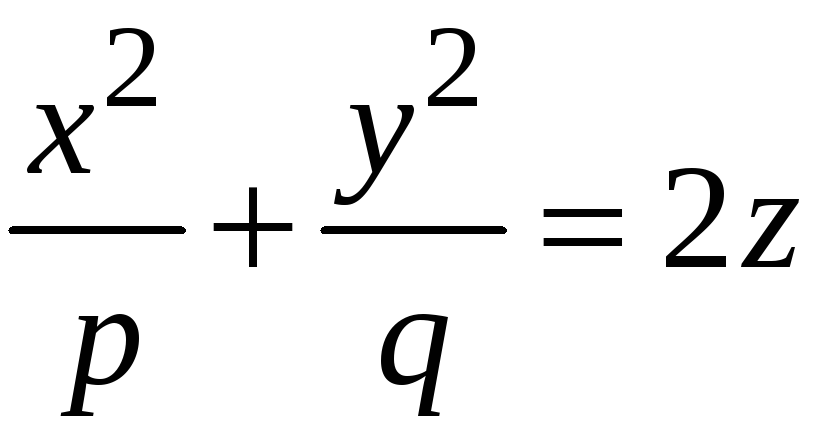 ,
,
![]() ,
или
,
или
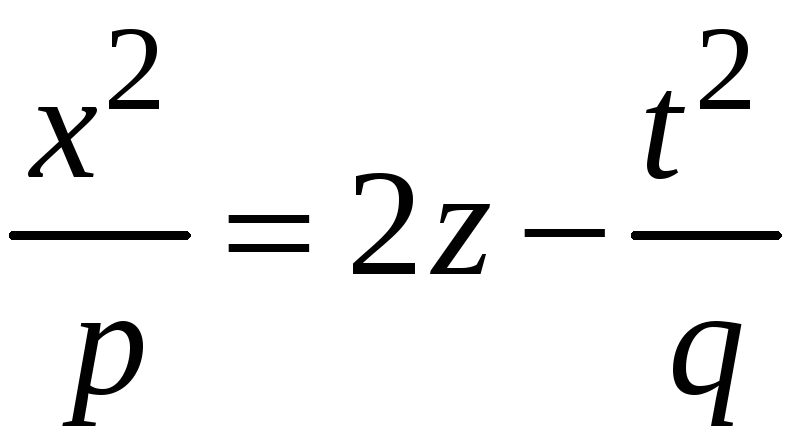 ,
,
![]() ,
или:
,
или:
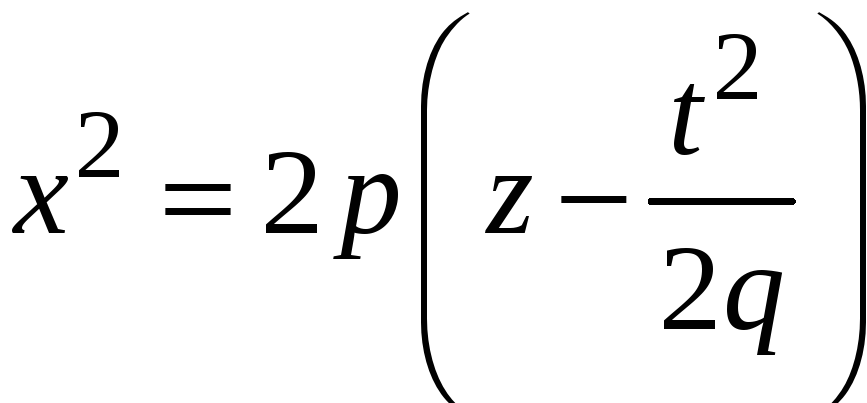 ,
,
![]() .
.
Эти уравнения
выражают параболу с вершиной
 ,
ось которой выражается уравнением:
,
ось которой выражается уравнением:
![]() ,
,
![]() и одинаково направлена с осью
и одинаково направлена с осью
![]() .
Параметр параболы
.
Параметр параболы
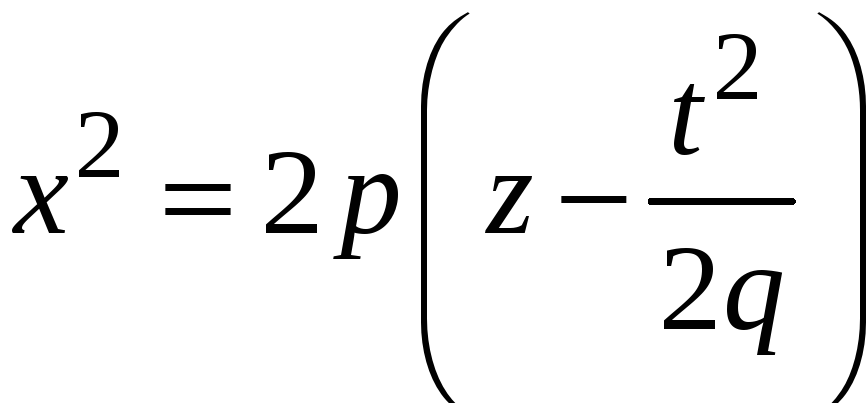 ,
,
![]() равен
равен
![]() ,
т.е. параметру главного сечения
эллиптического параболоида плоскостью
,
т.е. параметру главного сечения
эллиптического параболоида плоскостью
![]() .
.
Аналогичная
картина получается и для сечений
эллиптического параболоида (1) плоскостями,
параллельными плоскости
![]() .
.
Таким образом,
эллиптический параболоид может быть
образован параллельным переносом
параболы
![]() по параболе
по параболе
![]() ,
а оси этих парабол параллельны и одинаково
направлены (См. рис. 208).
,
а оси этих парабол параллельны и одинаково
направлены (См. рис. 208).
Эллиптический
параболоид является образом параболоида
вращения
![]() при равномерном сжатии пространства:
при равномерном сжатии пространства:
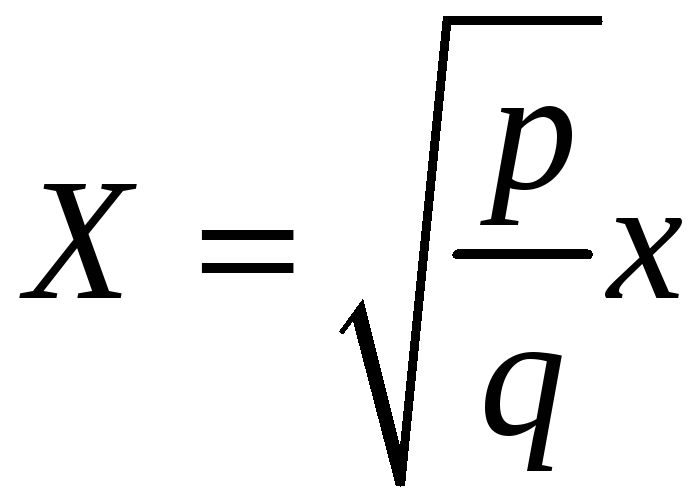 ,
,
![]() ,
,
![]() к плоскости
к плоскости
![]() (коэффициент сжатия
(коэффициент сжатия
![]() ).
).
§ 134. Гиперболический параболоид.
Определение. Гиперболическим параболоидом называется поверхность, уравнение которой в неко-торой специально выбранной прямоугольной системе
координат, имеет
вид:
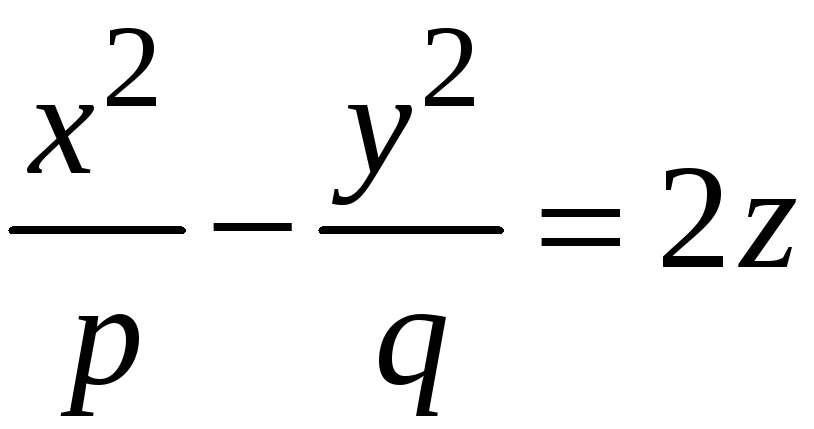 ,
(3)
,
(3)
где
![]() ,
,
![]() .
Для гиперболического параболоида (3)
плоскости
.
Для гиперболического параболоида (3)
плоскости
![]() и
и
![]() являются плоскостями симметрии, а ось
являются плоскостями симметрии, а ось
![]() осью симметрии.
осью симметрии.
Ось симметрии для гиперболического параболоида называется просто его осью. Точка в которой ось гиперболического параболоида пересекает эту поверхность, называется вершиной. Гиперболический параболоид имеет вершину в начале координат.
Плоскости
![]() и
и
![]() ,
являющиеся для гиперболического
параболоида плоскостями симметрии,
называются главными плоскостями
гиперболического параболоида.
,
являющиеся для гиперболического
параболоида плоскостями симметрии,
называются главными плоскостями
гиперболического параболоида.
Плоскость
![]() пересекает гиперболический пара-болоид
(3) по прямым:
пересекает гиперболический пара-болоид
(3) по прямым:
 ;
или
;
или
 ,
,
![]() ;
и
;
и
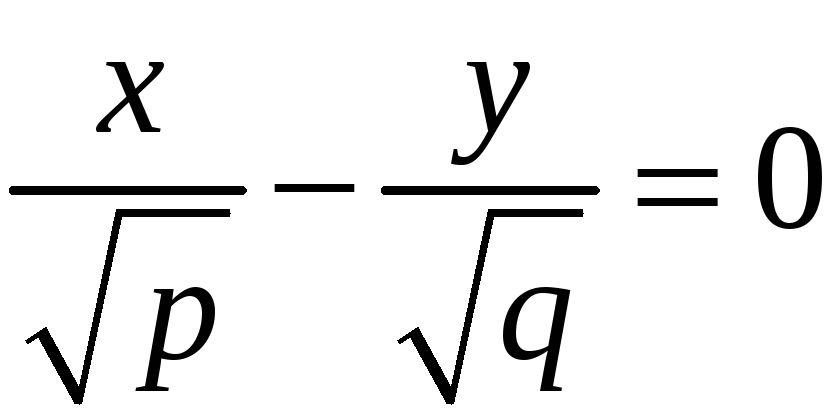 ,
,
![]() .
.
Плоскость
![]() ,
параллельная плоскости
,
параллельная плоскости
![]() ,
пересекает гиперболический параболоид
по гиперболе
,
пересекает гиперболический параболоид
по гиперболе
![]() :
:
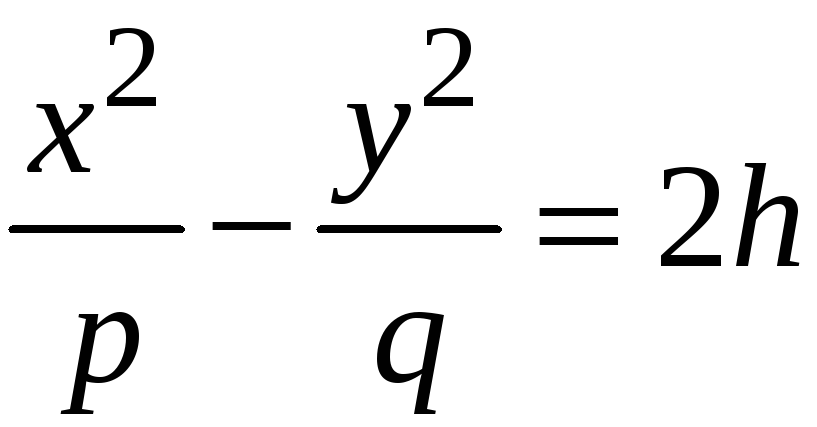 ,
,
![]() .
(4)
.
(4)
Если
![]() ,
то эти уравнения можно параписать в
виде:
,
то эти уравнения можно параписать в
виде:
 ,
,
![]() .
Это гипербола, расположенная в плоскости
.
Это гипербола, расположенная в плоскости
![]() с центром в точке
с центром в точке
![]() ,
действительная ось которой параллельна
оси
,
действительная ось которой параллельна
оси
![]() ,
а мнимая - параллельна оси
,
а мнимая - параллельна оси
![]() .
.
Если
![]() ,
то уравнения линии сечения можно
представить в виде:
,
то уравнения линии сечения можно
представить в виде:
 ,
,
![]() .
Это гипербола, расположенная в плоскости
.
Это гипербола, расположенная в плоскости
![]() с центром в точке
с центром в точке
![]() ,
действительная ось которой параллельна
оси
,
действительная ось которой параллельна
оси
![]() ,
а мнимая - параллельна оси
,
а мнимая - параллельна оси
![]() .
.
Асимптоты всех
гипербол, получающихся при пересечении
гиперболического параболоида (3)
плос-костями
![]() ,
,
![]() параллельны прямым, по которым этот
параболоид пересекается с плоскостью
параллельны прямым, по которым этот
параболоид пересекается с плоскостью
![]() .
.
Плоскость
![]() пересекает гиперболический параболоид
(3) по параболе
пересекает гиперболический параболоид
(3) по параболе
![]() :
:
![]() ,
,
![]() ,
а плоскость
,
а плоскость
![]() по параболе
по параболе
![]() :
:
![]() ,
,
![]() .
.
Мы видим, что
числа
![]() и
и
![]() являются параметрами парабол, получающихся
в сечении гиперболического параболоида
(3) его главными плоскостями.
являются параметрами парабол, получающихся
в сечении гиперболического параболоида
(3) его главными плоскостями.
Рассмотрим сечения
гиперболического параболоида (3)
плоскостями, параллельными плоскостям
![]() ,
т.е. плоскостями, выражаемыми уравнением
,
т.е. плоскостями, выражаемыми уравнением
![]() .
.
Уравнение линии сечения будет следующим:
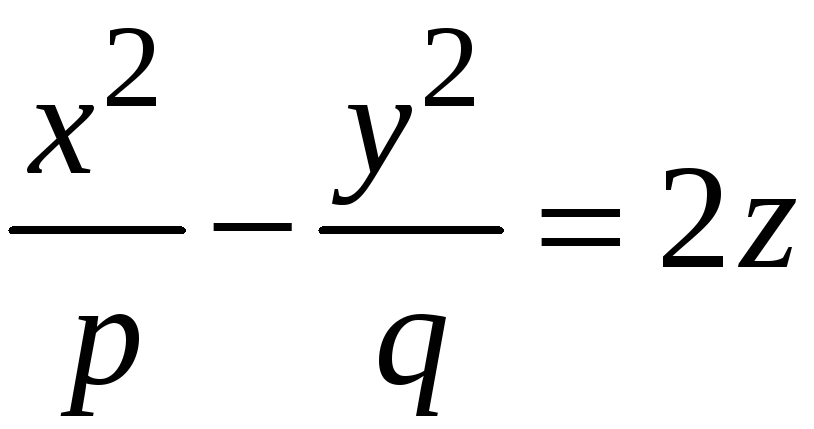 ,
,
![]() ,
или
,
или
 ,
,
![]() ,
или:
,
или:
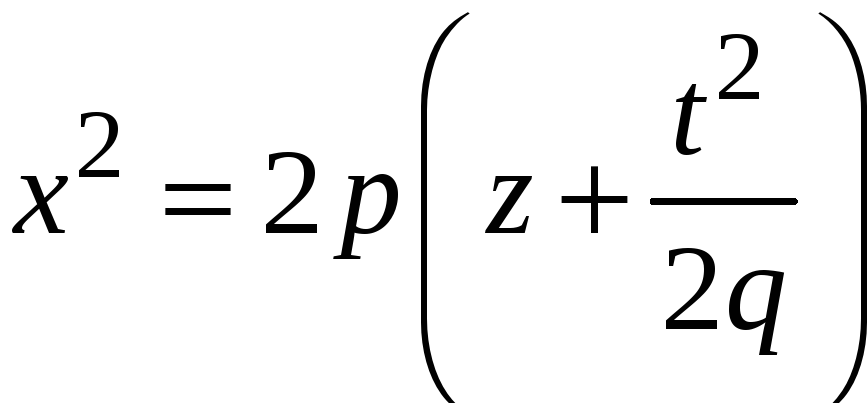 ,
,
![]() .
.
Эти уравнения
выражают параболу
![]() с вершиной в точке
с вершиной в точке
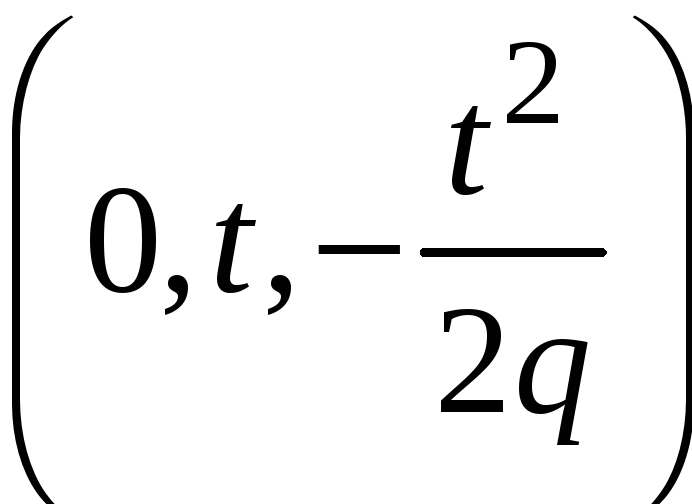 ,
ось которой выражается уравнением:
,
ось которой выражается уравнением:
![]() ,
,
![]() а направление совпадает с положительным
направлением оси
а направление совпадает с положительным
направлением оси
![]() .
Параметр параболы
.
Параметр параболы
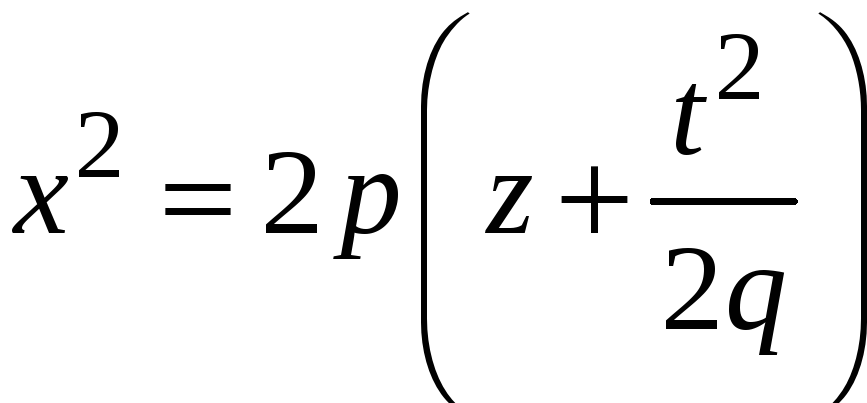 ,
,
![]() равен
равен
![]() ,
т.е. параметру главного сечения
гиперболического параболоида плоскостью
,
т.е. параметру главного сечения
гиперболического параболоида плоскостью
![]() .
.
Аналогичная
картина получается и для сечений
гиперболического параболоида (3)
плоскостями, параллельными плоскости
![]() (См. рисю209)
(См. рисю209)
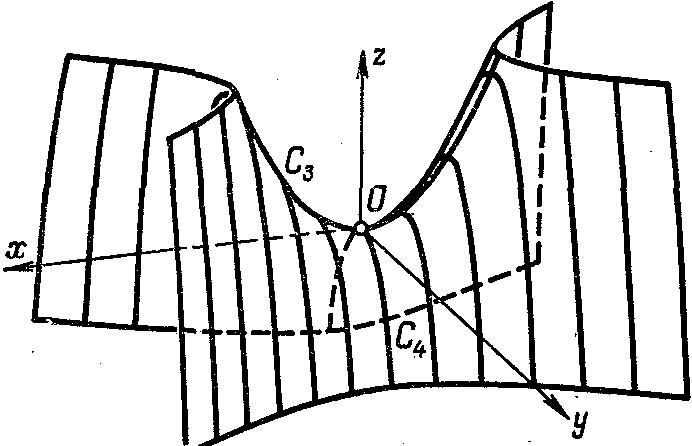
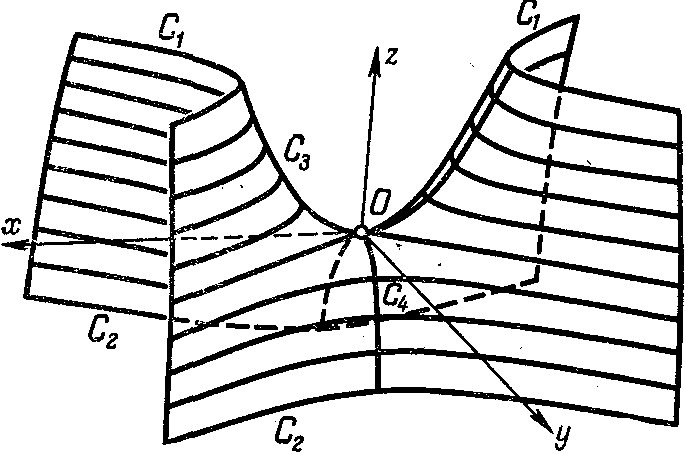
Рис. 209. Рис. 210.
Таким образом,
гиперболический параболоид может быть
образован параллельным переносом
параболы
![]() при котором вершина параболы
при котором вершина параболы
![]() перемещается по параболе
перемещается по параболе
![]() .
Плоскость параболы
.
Плоскость параболы
![]() перпендикулярна плоскости параболы
перпендикулярна плоскости параболы
![]() ,
а оси этих парабол параллельны и
противоположно направлены (См. рис.
208).
,
а оси этих парабол параллельны и
противоположно направлены (См. рис.
208).
§ 135. Цилиндры второго порядка.
Существуют три типа цилиндров второго порядка:
1. Эллиптический:
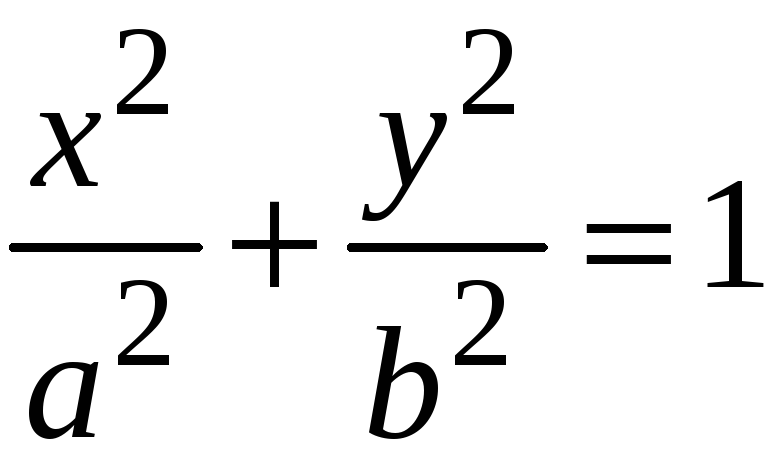 ;
(Рис. 211.) (5)
;
(Рис. 211.) (5)
2. Гиперболический:
 ;
(Рис. 212.) (6)
;
(Рис. 212.) (6)
3. Параболический:
![]() .
(Рис. 213.) (7)
.
(Рис. 213.) (7)

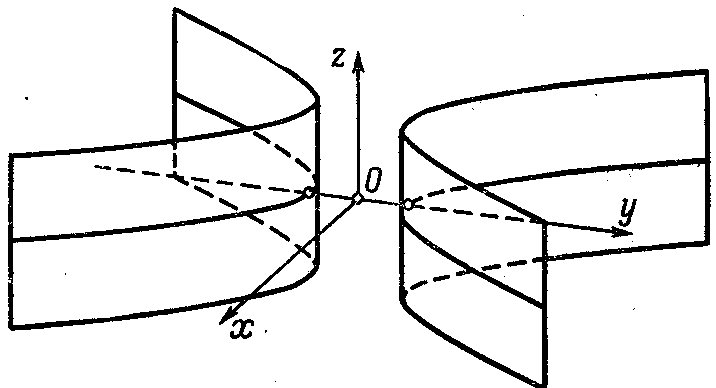
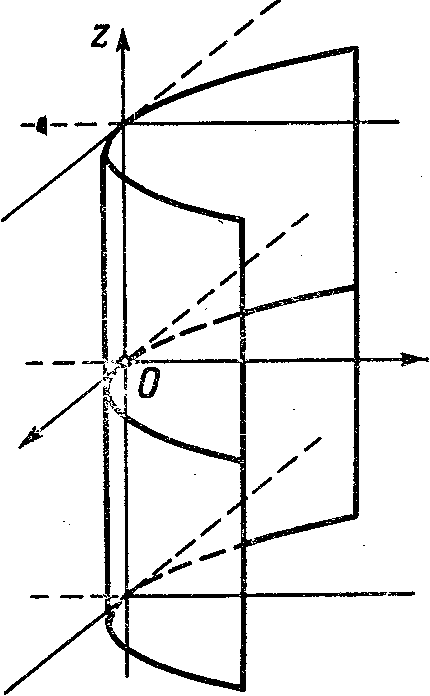
Рис. 211. Рис. 212. Рис. 213.
Эллиптический, гиперболический и параболический цилиндры суть поверхности, образованные прямыми линиями, проходящими через точки эллипса, гиперболы и параболы перпендикулярно плоскости каждой из этих линий. Эти линии - эллипс, гипербола и парабола называются направляющими, а прямые - лежащие на поверхности цилиндра, - его образующими. Для цилиндров, заданных уравнениями (5), (6), (7), направляющими являются соответственно:
Эллипс
 ,
,
![]() .
.
Гипербола
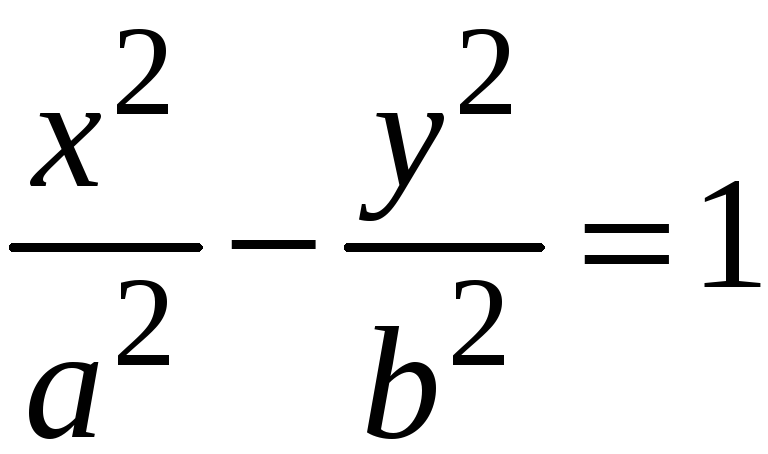 ,
,
![]() .
.
Парабола
![]() ,
,
![]() .
.
И образующие
параллельны оси
![]() .
.
§ 136. Прямолинейные образующие однополостного гиперболоида и гиперболического параболоида.
Мы видели, что конические и цилиндрические поверхности образуются при движении прямой линии. Конические поверхности - это поверхности, образованные движением прямой линии через фиксированную точку - вершину конической поверхности.
Цилиндрические поверхности - это поверхности, образованные движением прямой, параллельной одному и тому направлению.
Но поверхности могут быть образованы и движением прямой линии в пространстве совершенно произвольно. такие поверхности, образованные движущейся прямой называются линейчатыми поверхностями.
Так вот однополостный гиперболоид и гиперболический параболоид являются линейчатыми поверхностями. То есть образуются движением прямой линии в пространстве.
Чтобы убедиться
в этом, рассмотрим однополостный
гиперболоид, заданный свим каноническим
уравнением:
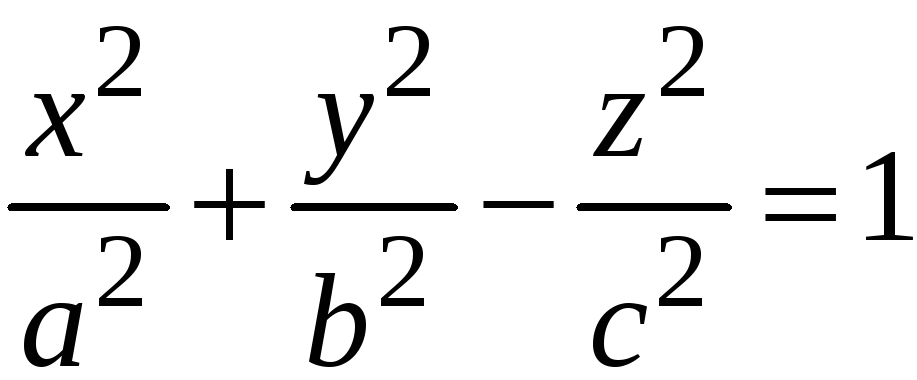 .
(8)
.
(8)
Перенесём
![]() в правую часть:
в правую часть:
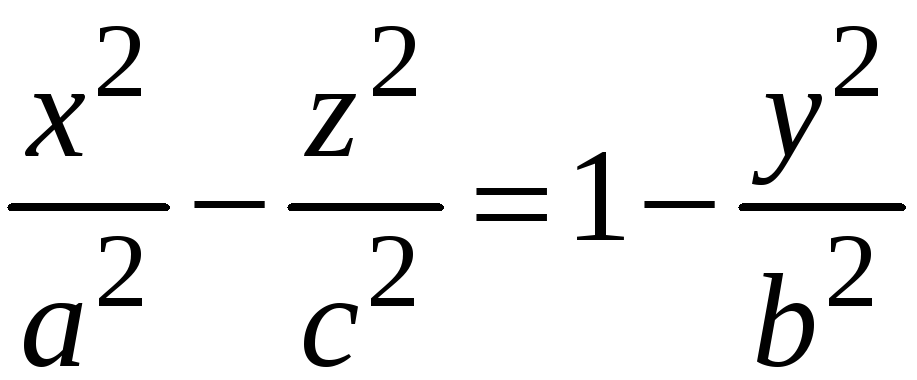 .
Справа и слева получились разности
квадратов. Преобразуем:
.
Справа и слева получились разности
квадратов. Преобразуем:
 .
(9) При любом значении
параметра
.
(9) При любом значении
параметра
![]() система уравнений:
система уравнений:
 (10)
(10)
представляет собой
общие уравнения прямой. эта прямая при
любом
![]() принадлежит однополостному гиперболоиду,
поскольку при
принадлежит однополостному гиперболоиду,
поскольку при
![]() уравнение (9) гиперболоида получается
перемножением системы (10) и сокращением
на
уравнение (9) гиперболоида получается
перемножением системы (10) и сокращением
на
![]() .
.
Таким образом
однополостному гиперболоиду принадлежит
бесконечно много прямых, описываемых
общими уравнениями (10). Если к этим прямым
добавить ещё одну прямую:
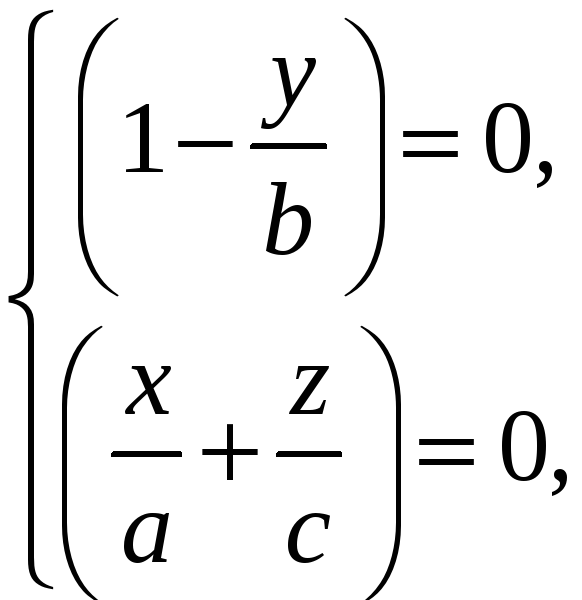 которая соответствует значению
которая соответствует значению
![]() (эти точки лежат на горловом эллипсе),
то через каждую точку однополостного
гиперболоида будет проходить одна
прямая, лежащая на гиперболоиде.
(эти точки лежат на горловом эллипсе),
то через каждую точку однополостного
гиперболоида будет проходить одна
прямая, лежащая на гиперболоиде.
Итак, гиперболоид представляет собой множество прямых, описываемых уравнениями (10). (Здесь в (10) прямая задаётся пересечением двух плоскостей). Эти прямые называются прямолинейными образующими однополостного гиперболоида.
Однополостный
гиперболоид имеет также второе семейство
прямолинейных образующих, которое
описывается системой уравнений: 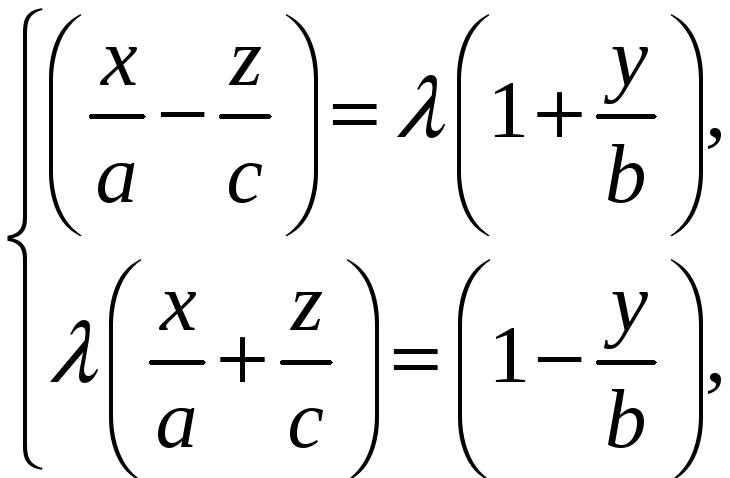 аналогичной (10) с тем соглашением о
значениях параметра
аналогичной (10) с тем соглашением о
значениях параметра
![]() (Рис. 214).
(Рис. 214).

Рис. 214.
Гиперболический
параболоид также может быть образован
движением прямой линии в
пространстве. Уравнение гиперболического
параболоида
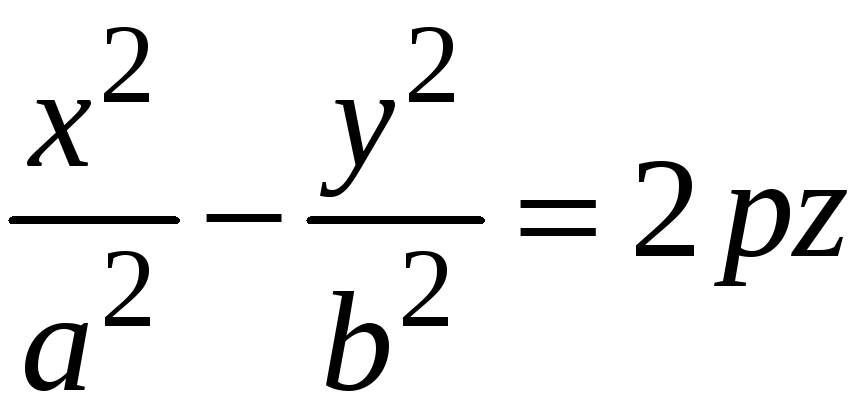 преобразуем к виду
преобразуем к виду
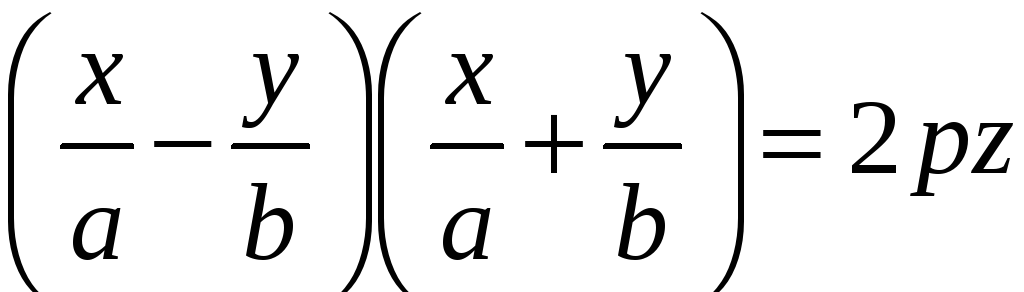 ,
Также как и в случае однополостного
гиперболоида, это уравнение можно
"расщепить" в систему двух линейных
уравнений:
,
Также как и в случае однополостного
гиперболоида, это уравнение можно
"расщепить" в систему двух линейных
уравнений:
 или
или
 Каждая из этих систем задаёт
семейство прямолинейных образующих
гиперболического параболоида.
Каждая из этих систем задаёт
семейство прямолинейных образующих
гиперболического параболоида. 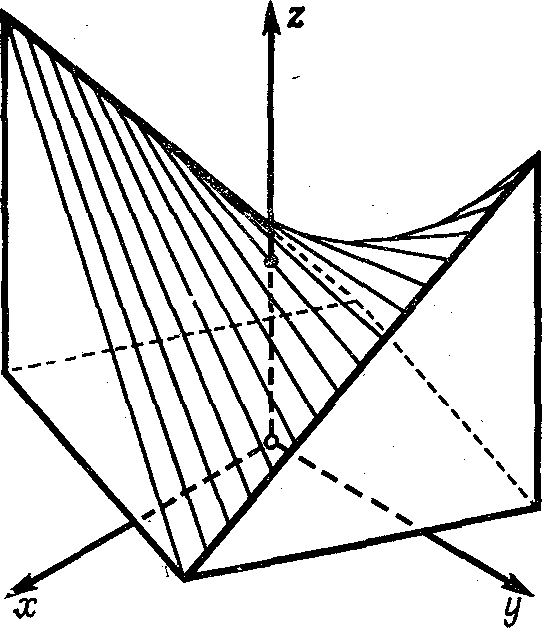 (
(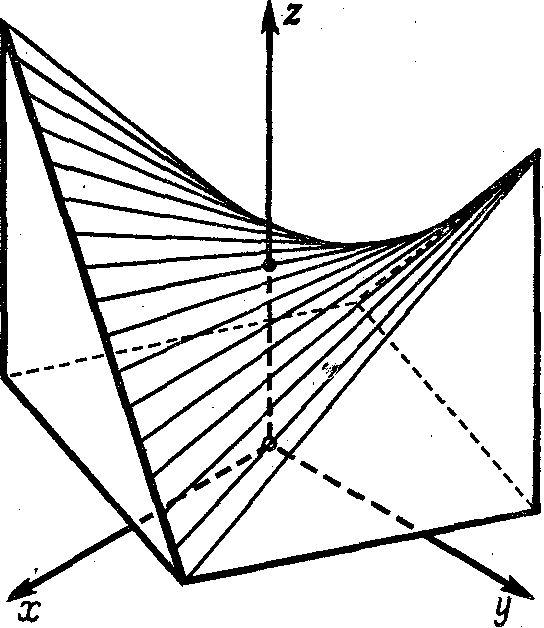 См.
рис.215)
См.
рис.215)
Рис. 215.
