Аналитическая геометрия.

Глава 11. Линии второго порядка, заданные общими уравнениями Лекция 10.

На прошлой лекции мы установили, что если линия второго порядка, задана относительно ОДСК общим уравнением

то уравнение диаметра, сопряжённого хордам неасимптотического направления имеет вид:

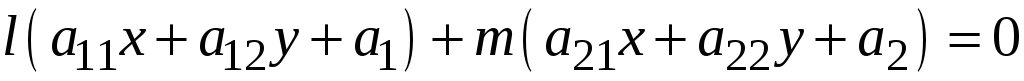, а его направляющий вектор имеет координаты: , .

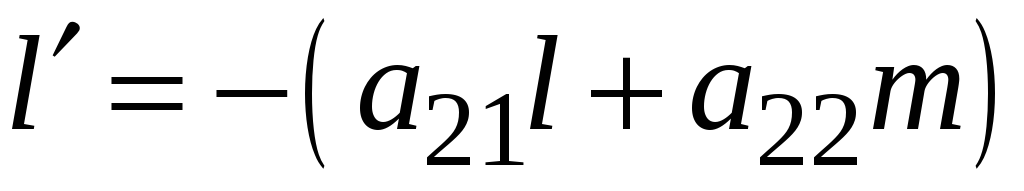§ 147. Касательная к линии второго порядка

Пусть относительно ОДСК на плоскости задана линия второго порядка общим уравнением (1). Будем называть точку 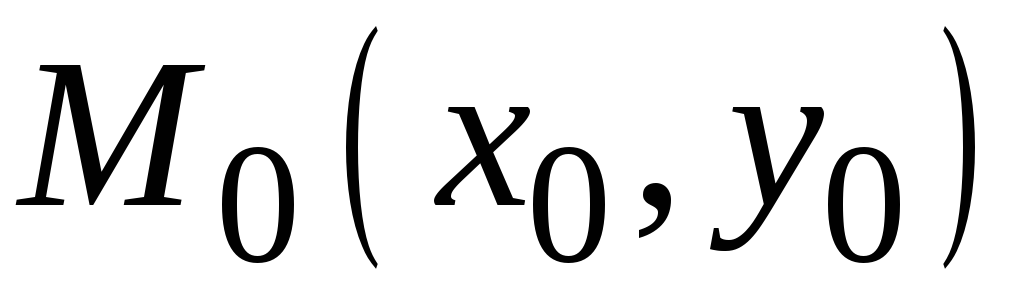, лежащую на этой линии

неособой, если среди чисел и есть хотя бы одно, не равное нулю. Ясно, что точка , лежащая на линии (1), является особой тогда и только тогда, она является центром линии (1).

Таким образом, среди линий эллиптического типа только линия, распадающаяся на две мнимые пересекающиеся прямые имеет особую точку (это точка их пересечения); среди линий гиперболического типа особую точку имеет пара пересекающихся прямых (это также точка их пересечения) и, наконец, среди линий параболического типа особые точки имеет пара совпадающих прямых (особыми точками являются все точки прямой, с которой совпадают рассматриваемые прямые).

Определение. Касательной к линии второго порядка в неособой точке, лежащей на этой линии, называется прямая, проходящая через эту точку, пересекающая данную линию в двукратной точке, или совпадающая с прямой, входящей в состав данной линии.

Теорема 1. Пусть 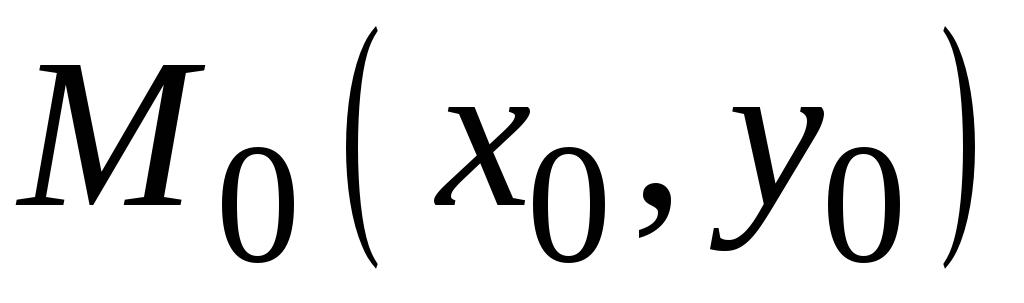- неособая точка линии второго порядка, заданной относительно ОДСК общим уравнением (1). Тогда уравнение касательной к этой линии в точке имеет вид:

Доказательство. Рассмотрим уравнение прямой

, ,

проходящей через данную неособую точку М₀ линии (1). Подставляя в уравнение (1) , вместо и , получим:

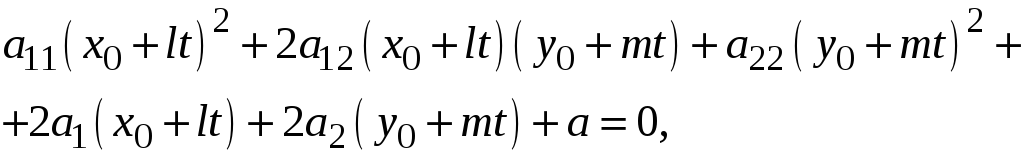
или, раскрывая скобки:

Но по предположению точка 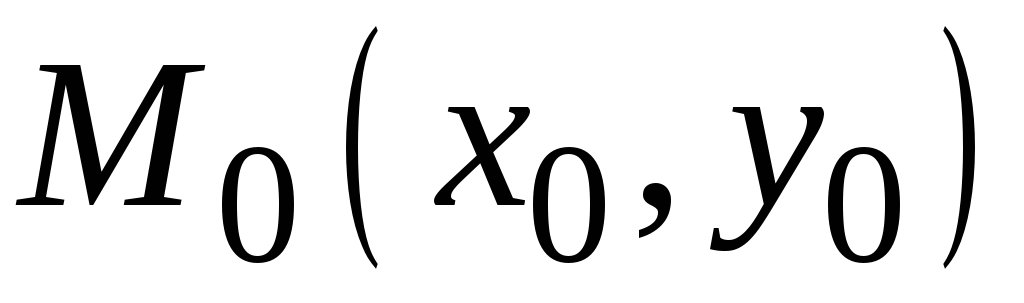лежит на данной линии, поэтому:

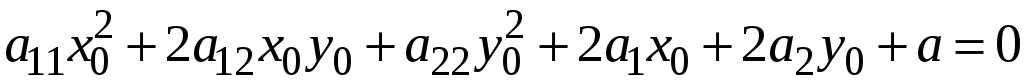и уравнение (3) принимает вид:

Одним из корней этого уравнения является ; при этом из соотношений , находим: , , т.е. координаты точки М₀.

Для того, чтобы прямая (3) являлась касательной к линии (1), необходимо и достаточно, чтобы уравнение (4) имело и второй корень, равный нулю, а для этого необходимо и достаточно, чтобы было выполнено условие:

Таким образом, координаты направляющего вектора касательной будут такими:

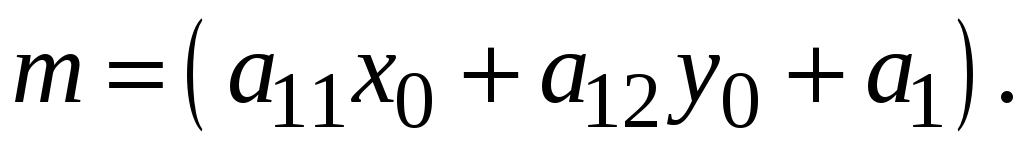, (5)

(Этот вектор ненулевой, т.к. точка по предположению неособая (а по определению неособой точки, числа и 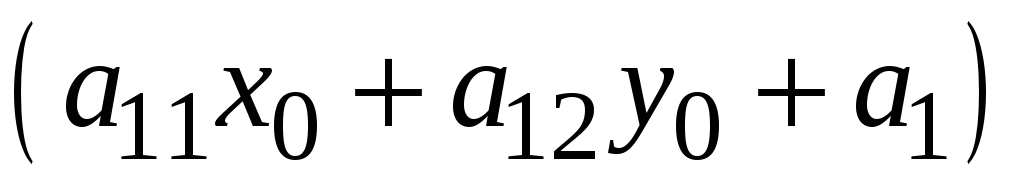не должны одновременно обращаться в нуль).

Если вектор , координаты которого определяются соотношениями (5), неасимптотического направления, т.е. 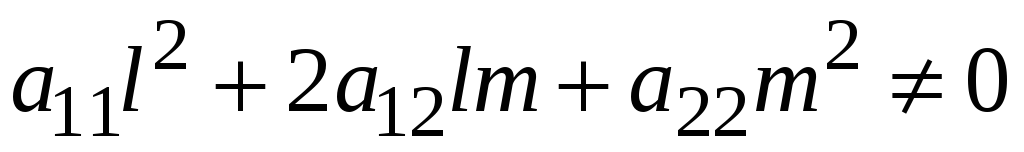, то уравнение (4) имеет двукратный корень ; а если вектор имеет асимптотическое направление, то есть , то уравнение (4) обращается в тождество, в этом случае прямая , входит в состав данной линии (1) и, значит, согласно принятому определению, является касательной к линии (1) в точке .

Итак, уравнения касательной к линии (1) в её неособой точке имеют вид: , ,

или

или

и, так как

то окончательно

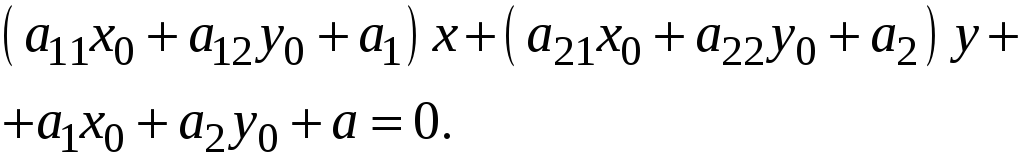ЧТД.

Теорема 2. Пусть относительно ОДСК линия второго порядка задана общим уравнением (1). Пусть диаметр (6) этой линии, сопряженный хордам, имеющим неасимптотическое направление , пересекает рассматриваемую линию в неособой точке . Тогда касательная к этой линии в точке М₀ параллельна хордам, которым сопряжён диаметр (6).

Доказательство. Так как диаметр (6) проходит через точку , то:

и так как неособая точка рассматриваемой линии, то можно считать, что:

, ,

а это координаты направляющего вектора касательной к рассматриваемой линии второго порядка в неособой точке (смотрите выше формулы (5)). ЧТД.

Замечание. Данное в этом параграфе определение касательной к линии второго порядка в её неособой точке совпадает с определением касательной линии, которое даётся в курсе математического анализа. Здесь линия задана уравнением вида . Функция при , обращается в нуль, а частные производные от неё по и , т.е. и , согласно условию теоремы 1 одновременно в нуль не обращаются. Функция двух переменных от и , значит уравнение касательной к линии можно записать в виде (как известно из курса матанализа):

. В нашем случае:

что совпадает с выведенным выше уравнением.