§ 117. Уравнение гиперболы, отнесённой к асимптотам.

Перепишем уравнения асимптот гиперболы в виде . Введём новую систему координат, принимая за начало координат по-прежнему центр гиперболы, а за масштабные векторы осей и - единичные направляющие векторы асимптот: 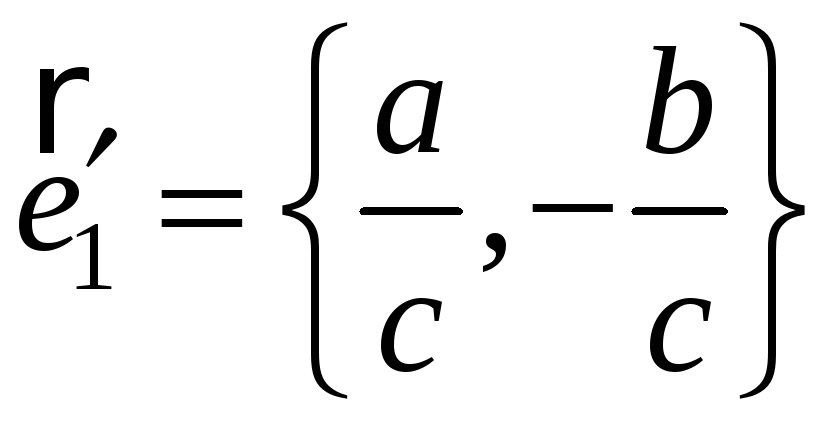, 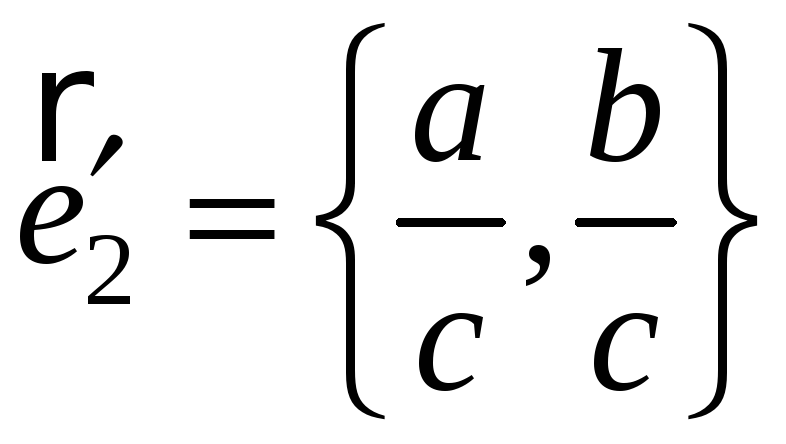. Тогда формулы преобразования координат будут иметь вид: , .

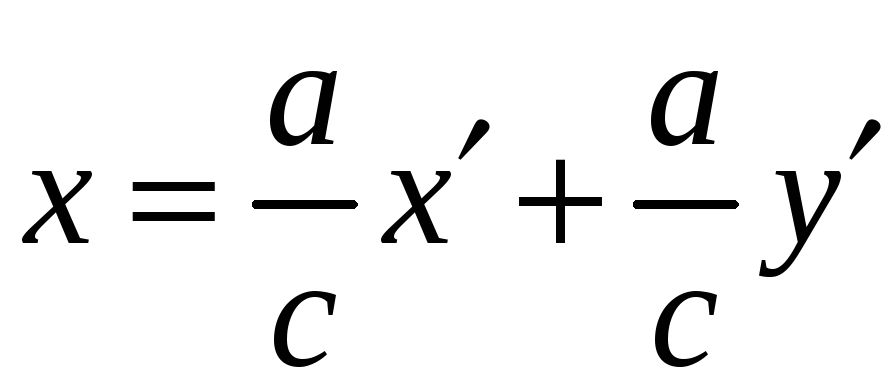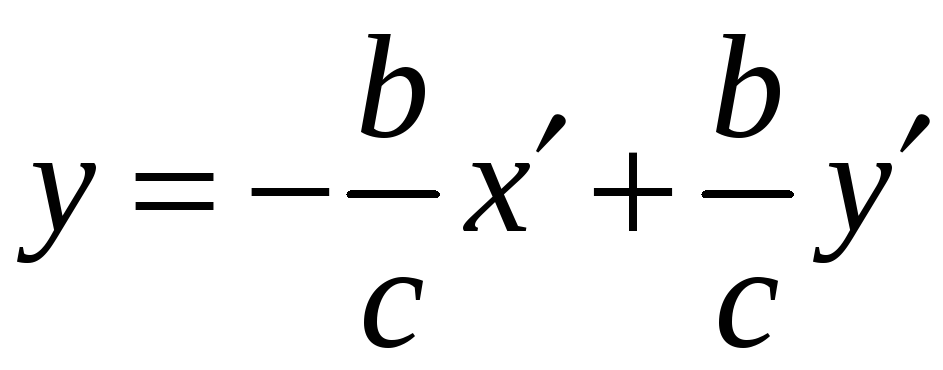Следовательно 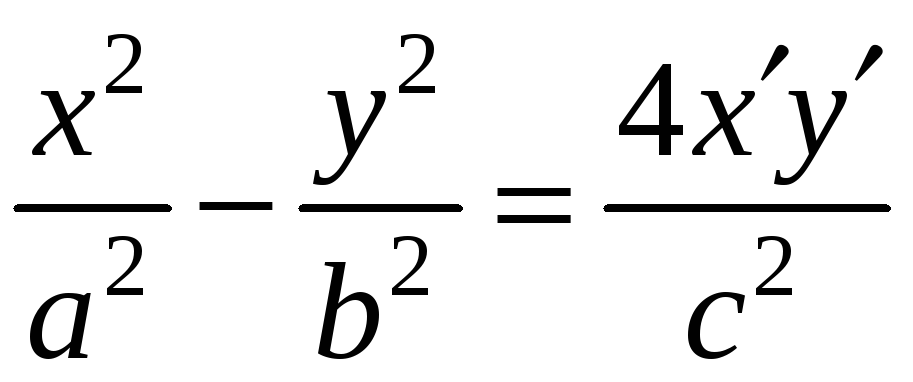. И, значит, уравнение гиперболы, отнесённой к асимптотам, имеет вид: .

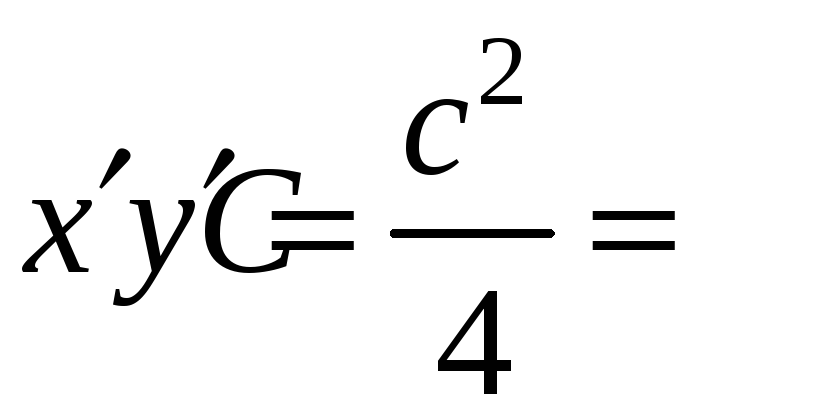Обратно, при любом уравнение определяет гиперболу; осями координат служат её асимптоты и если ввести новую Декартовую прямоугольную систему координат, принимая за новые оси ориентированные прямые, являющиеся биссектрисами углов между асимптотами и , то получим каноническое уравнение гиперболы.

Сопряжённые гиперболы определяются уравнениями: , .

§ 118. Касательная к гиперболе.

Уравнение касательной к гиперболе, заданной каноническим уравнением 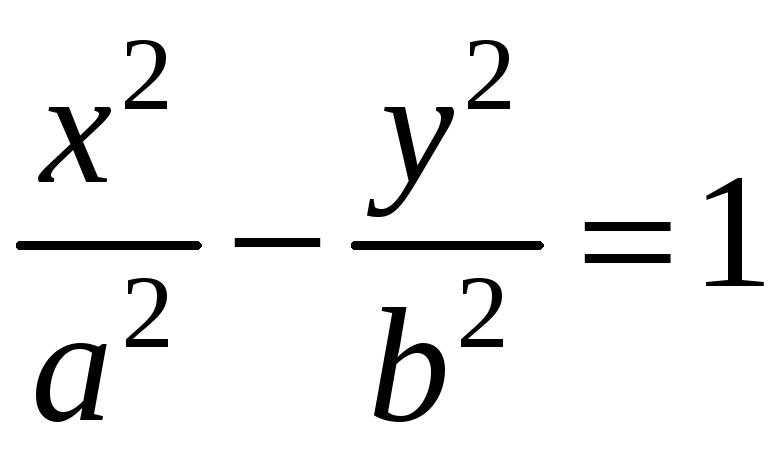в точке , лежащей на этой гиперболе, можно записать в виде (мы знаем, что уравнение касательной - это уравнение следующего вида ).

Для гиперболы это:

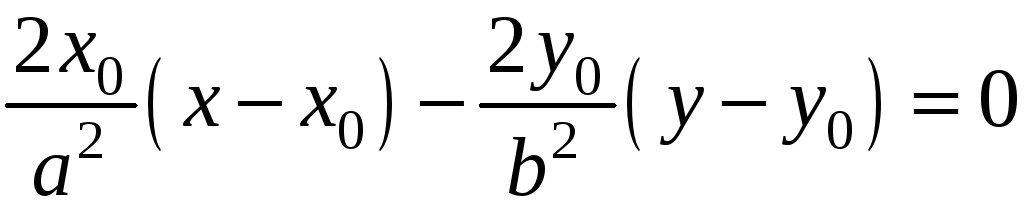или .

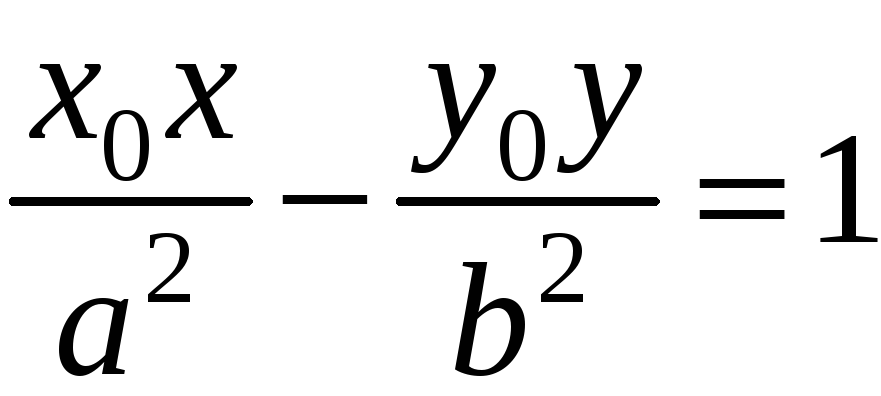§ 119. Оптическое свойство гиперболы.

Теорема. Касательная к гиперболе в произвольной её точке является биссектрисой внутреннего угла треугольника , имеющего своими вершинами фокусы гиперболы и данную точку .(См. рис. 173)

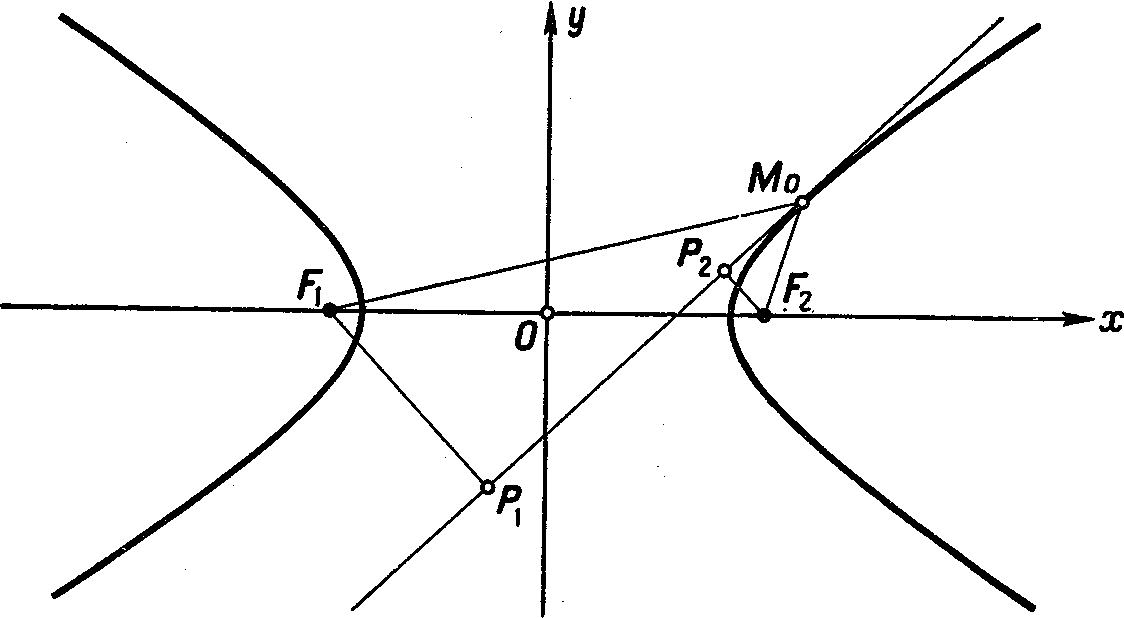Рис. 173.

Доказательство. Опустим из фокусов и перпендикуляры и на касательную. Также как и для эллипса доказывается, что 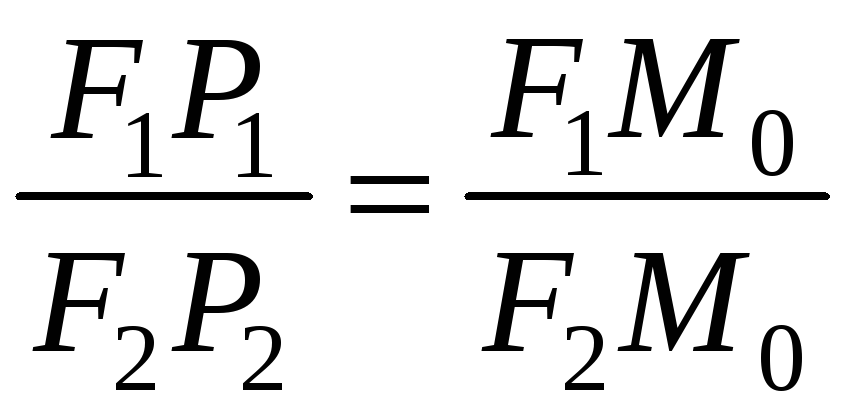. Поэтому и, следовательно, .

Результаты подстановок координат фокусов и в выражение 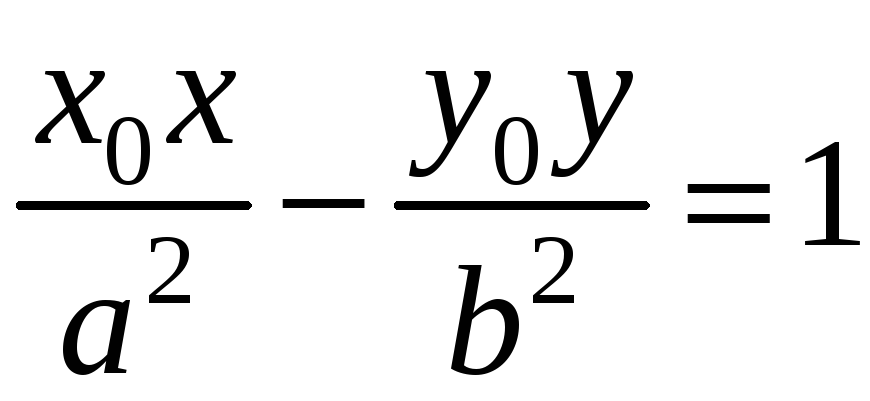- числа разных знаков, откуда следует, что фокусы гиперболы лежат по разные стороны от любой касательной к ней.

Указанное геометрическое свойство позволяет построить касательную к гиперболе в произвольной точке : точку соединяем с фокусами и гиперболы и угол делим пополам; биссектриса этого угла и является касательной к гиперболе в точке .

Доказанной теореме можно придать оптическое истолкование, аналогичное как для эллипса. Луч света, пущенный из фокуса , отразившись от зеркальной поверхности гиперболы, будет направлен по прямой (См. рис.)

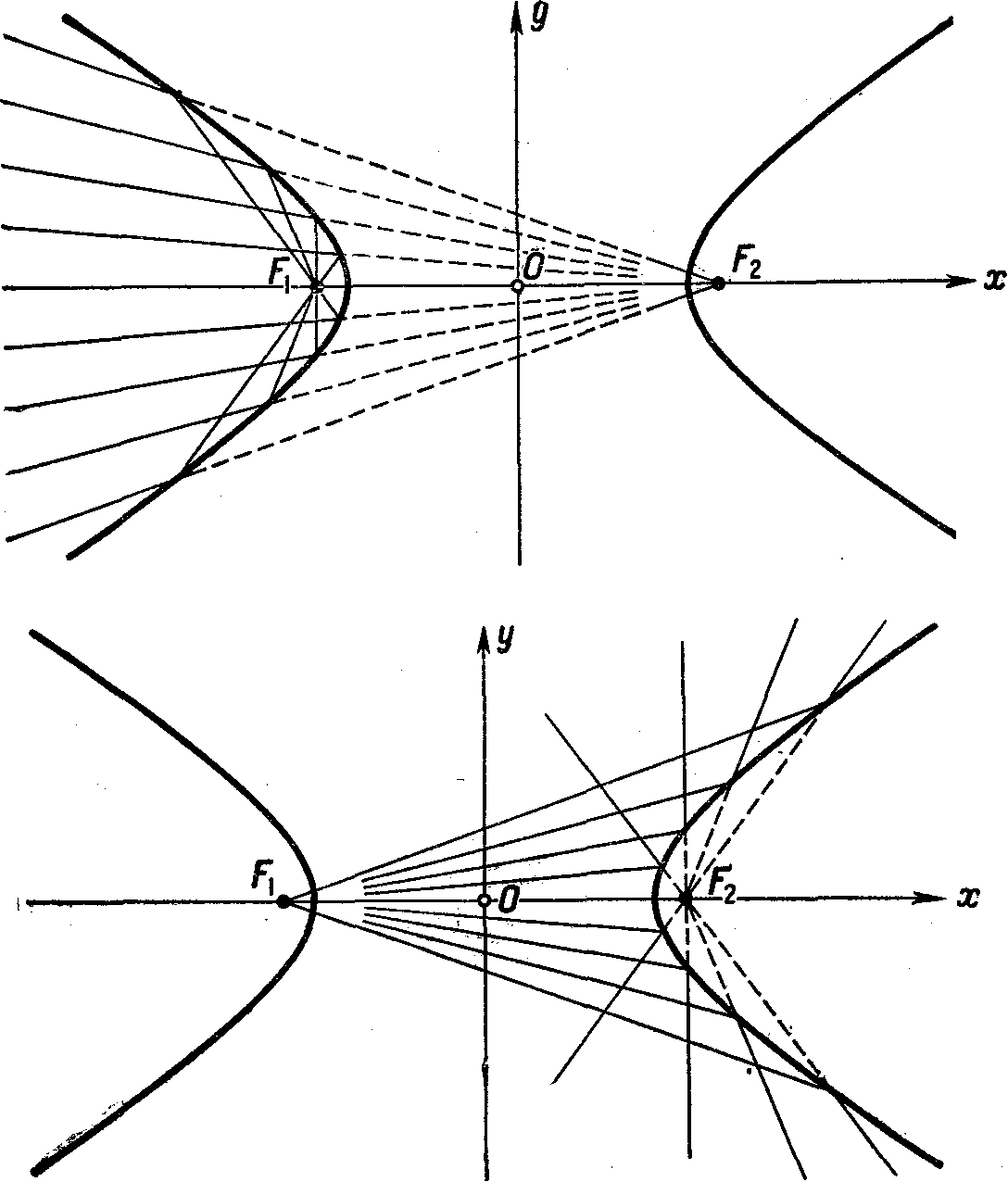Рис. 174