§ 162. Эллиптические, гиперболические или параболические точки поверхности второго порядка.
1. Пусть касательная
плоскость к поверхности второго порядка
в точке
пересекает её по двум мни-мым пересекающимся
прямым. В этом случае точка
называется эллиптической точкой
поверхности.
2. Пусть касательная
плоскость к поверхности второго порядка
в точке
пересекает её по двум действительным
прямым, пересекающимся в точке касания.
В этом случае точка
называется гиперболической точкой
поверхности.
3. Пусть касательная
плоскость к поверхности второго порядка
в точке
пересекает её по двум совпадающим
прямым. В этом случае точка
называется параболической точкой
поверхности.
Теорема
4. Пусть
поверхность второго порядка относительно
ОДСК задана уравнением (1) и данное
уравнение (1) является уравнением
действительной нераспадающейся
поверхностью второго порядка. Тогда,
если
;
то все точки поверхности эллиптические.
Доказательство.
Введём новую систему координат
,
выбирая за начало координат любую
неособую точку
данной поверхности и располагая оси
и
в плоскости, касательной к поверхности
в точке
.
Уравнение (1) в новой системе координат
преобразуется к виду:
где
.
Вычислим инвариант
для этого уравнения
.
Так как при
переходе от одной ОДСК к другой ОДСК
знак
не меняется, то знаки
и
противоположны, поэтому, если
,
то
;
и, как следует из классификации (см.§
161) касательная плоскость к поверхности
в точке
пересекает поверхность по двум мнимым
пересекающимся прямым, т.е.
-
эллиптическая точка.
Если
,
то
,
касательная плоскость к по-верхности
в точке
пересекает её по двум прямым, пересекающимся
в точке
;
точка
-
гиперболическая.
Если, наконец,
,
то и
,
касательная плоскость к поверхности в
точке
пересекает её по паре совпадающих
прямых; точка
-
параболическая.
Ограничиваясь
действительными нераспадающимися
поверхностями второго порядка и вычисляя
,
например, по каноническим уравнениям
этих поверхностей, убедимся в том, что:
1) Эллипсоид, двуполостный гиперболоид и эллиптический параболоид состоят из эллиптических точек.
2) Однополостный гиперболоид и гиперболический параболоид состоят из гиперболических точек.
3) Действительный конус второго порядка (вершина исключается), эллиптический (действительный), гиперболический и параболический цилиндры состоят из параболических точек.
Параболический цилиндр.
Чтобы определить расположение параболического цилиндра, достаточно знать:
плоскость симметрии, параллельную образующим цилиндра;
касательную плоскость к цилиндру, перпендикулярную к этой плоскости симметрии;
вектор, перпендикулярный к этой касательной плоскости и направленный в сторону вогнутости цилиндра.
В случае, если общее уравнение определяет параболический цилиндр, оно может быть переписано в виде:
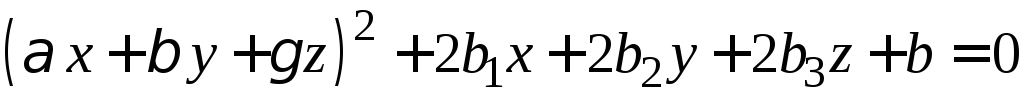
или
Подберем m так, чтобы плоскости
были бы взаимно перпендикулярными:
откуда
При этом значении m плоскость
будет плоскостью симметрии, параллельной образующим цилиндра.
Плоскость
будет касательной плоскостью к цилиндру, перпендикулярной к указанной плоскости симметрии, а вектор
будет перпендикулярен к найденной касательной плоскости и направлен в сторону вогнутости цилиндра.