§ 160. Касательная плоскость к поверхности второго порядка

Определение. Точка , лежащая на поверхности второго порядка, заданной относительно ОДСК общим уравнением (1) называется неособой, если среди трёх чисел:есть хотя бы одно, не равное нулю.

Таким образом, точка , лежащая на поверхности второго порядка, является не особой тогда и только тогда, когда она является её центром, иначе, когда поверхность коническая, а точка- вершина этой поверхности.

Определение. Касательной прямой к поверхности второго порядка в данной на ней не особой точке называется прямая, проходящая через эту точку, пересекающая поверхность второго порядка в дву-кратной точке или являющаяся прямолинейной образующей поверхности.

Теорема 3. Касательные прямые к поверхности второго порядка в данной на ней не особой точке лежат в одной плоскости, называемой касательной плоскостью к поверхности в рассматриваемой точке. Уравнение касательной плоскости имеет

вид:

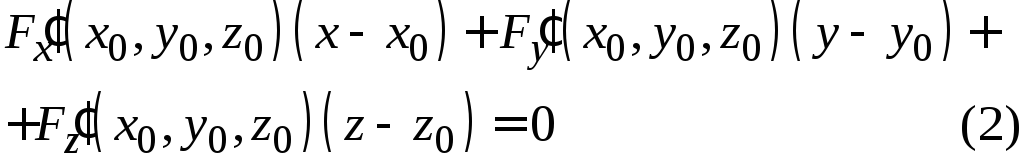
Доказательство. Пусть ,,параметрические уравнения прямой, проходящей через неособую точкупо-верхности второго порядка, заданной уравнением (1). Подставляя в уравнение (1),,вместо,,, получим:

Так как точка лежит на поверхности (1), тои из уравнения (3) находим(это значениесоответствует точке). Для того, чтобы точка пересечения прямой с поверхностью (1) была двойной, или чтобы прямая целиком лежала на поверхности, необходимо и достаточно, чтобы выполнялось равенство:

Если при этом:

, то точка пересечения прямой линии с поверхностью (1) двойная. А если:

, то прямая целиком лежит на поверхности (1).

Из соотношений (4) и ,,следует, что координаты,,любой точки, лежащей на любой касательной к поверхности (1) удовлетворяют уравнению:

Обратно, если координаты какой-нибудь точки , отличной от, удовлетворяют этому уравнению, то координаты,,вектора, удовлетворяют соотношению (4), а это значит, что прямая- касательная к рассматриваемой поверхности.

Так как точка - неособая точка поверхности (1), то среди чисел,,есть по крайней мере одно, не равное нулю; значит уравнение (5) есть уравнение первой степени относительно. Это и есть уравнение плоскости, касательной к поверхности (1) в данной на ней не особой точке.

Исходя из канонических уравнений поверхностей второго порядка легко составить уравнения касательных плоскостей к эллипсоиду, гиперболоиду и т.д. в данной на них точке .

1). Касательная плоскость к эллипсоиду:

.

2 ). Касательная плоскость к одно и двуполостному гиперболоидам:

.

3 ). Касательная плоскость к эллиптическому и гиперболическому параболоидам:

.

§ 161. Пересечение касательной плоскости с поверхностью второго порядка.

Примем неособую точку поверхности второго порядка за начало координат ОДСК, осиирасположим в плоскости касательной к поверхности в точке. Тогда в общем уравнении поверхности (1) свободный член равен нулю:, а уравнение плос-кости, касающейся поверхности в начале координат, должно иметь вид:.

Но уравнение плоскости, проходящей через начало координат имеет вид: .

И, так как это уравнение должно быть эквивалентно уравнению , то,,.

Итак, в выбранной системе координат уравнение поверхности (1) должно иметь вид:

Обратно, если , то уравнение (6) является уравнением поверхности, проходящей через начало координат, а плоскость- касательная плоскость к этой поверхности в точке. Уравнение линии, по которой касательная плоскость к поверхности в точкепересекает поверхность (6) имеет вид:

; .

Если . Это инвариантв теории инвариантов для линий второго порядка. Уравнение(7)

- это же линия второго порядка. По виду этой линии инвариант , поэтому:

При здесь две мнимые пересекающиеся прямые.

При - две действительные пересекающиеся прямые.

Если , но хотя бы один из коэффициентов,,не равен нулю, то линия пересечения (7) - две совпадающие прямые.

Наконец, если , то плоскость

входит в состав данной поверхности, а сама поверхность распадается, следовательно, на пару плоскостей