Классическая парадоксальность туннельного эффекта.

Знаем, что полная энергия складывается из кинетической и потенциальной энергий:

Если , , но , то, согласно квантовой механике, обнаружить частицу за пределами потенциального барьера возможно. Но при этом, если посчитать из закона сохранения энергии кинетическую энергию, то

,

что, казалось бы, нарушает классический закон сохранения энергии.

Однако квантовая механика снимает этот парадокс.

Действительно, согласно соотношению неопределенности Гейзенберга: - одновременно точно определить координату и импульс, или функции от них зависящие, нельзя.

Хотя полная энергия является определенной величиной, но кинетическая энергия зависит только от импульса, а потенциальная энергия только от координат. Следовательно, невозможно внутри барьера определить одновременно точно кинетическую и потенциальную энергии. Этим положением и снимается парадоксальность туннельного эффекта.

Классическим гармоническим осциллятором называется материальная точка, находящаяся в поле действия квазиупругих сил.

Под действием таких сил частица попадает в потенциальное поле

Под действием таких сил частица начинает колебаться с частотой , следовательно

Мы будем рассматривать квантовый линейный осциллятор.

Квантовым гармоническим линейным осциллятором называется частица, колеблющаяся в поле действия квазиупругих сил. Полная энергия такой частицы определяется суммой кинетической и потенциальной энергий:

Чтобы решить задачу квантовой механики необходимо решить уравнение Шредингера: . Мы будем рассматривать одномерный случай, поэтому возьмем проекцию импульса на ось х.

;

(8.1) уравнение Шредингера для одномерного гармонического линейного осциллятора.

При этом волновая функция должна быть непрерывна, однозначно определятся из этого уравнения, и должна быть ограничена, т.е. на бесконечности не должна обращаться в 0. Для решения данного уравнения введем безразмерную переменную (8.2)

(8.3)

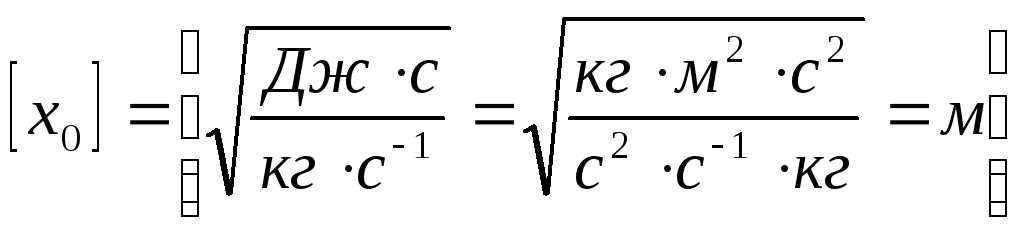
(8.2^’)

(8.4)

Подставим x₀ в явном виде

(8.4’)

(8.5) (8.6)

Для решения уравнения (8.6) введем подстановку: (8.7)

(8.8)

(8.8^’)

(8.8^’)

Решение данного уравнения будем искать в виде бесконечного ряда:

(8.9)

(8.10)

В первом слагаемом сдвинем сумму ряда на 2 единицы, т.е. вместо .

Во втором слагаемом внесем под знак суммы и суммирование распространим на k=0. В третьем слагаемом внесем под знак суммы.

(8.11)

Получили, что бесконечный ряд равен нулю. Для того, чтобы данный ряд был равен 0 для любых , необходимо, чтобы все коэффициенты этого ряда равнялись 0, т.е.

(8.12)

Мы получили рекуррентное соотношение между коэффициентами ряда и .

(8.12^’)

Т.е. мы можем определить либо все четные, либо все нечетные коэффициенты ряда.

Данное соотношение дает такие коэффициенты, что функция , следовательно , , ,что является физически

бессмысленно. Чтобы данное решение имело физический смысл, необходимо оборвать ряд, т.е. сделать функцию - полиномом.

Предположим, что для k=n коэффициенты , а коэффициенты , тогда

(8.13)

(8.14)

Т.е. из условия обрывания ряда мы получили полную энергию осциллятора

(8.15)

- полином (8.16)

Из выражения (8.15) видно, что пропорциональна n, n=0,1,2,3…; поэтому полная энергия осциллятора принимает дискретный ряд значений или квантуется. При этом n обозначает номер энергетического уровня и называется главным квантовым числом.

n=0 ; n=1 ; n=2

Мы видим, что полная энергия осциллятора в зависимости от главного квантового числа меняется с шагом . При n=0 энергия осциллятора не равна 0 и равна этот уровень является основным или низшим. Данный результат согласуется с соотношением неопределенности. Полная энергия:

Это говорит о том, что одновременно координата и импульс не могут обращаться в 0. Следовательно, одновременно и кинетическая и потенциальная энергия не может обращаться в 0,поэтому полная энергия осциллятора не может быть равной 0.

- полином Эрмита - Чебышева (8.16^’)

(8.17)

n=0

n=1

n=2

(8.7’)

(8.18)

Из (18) видим, что каждому энергетическому уровню соответствует своя волновая функция. Данная волновая функция записана с точностью до нормировочного множителя. Для каждой волновой функции с разными n нормировочный множитель оказывается одним и тем же: (8.19)

Он получается из условия нормировки:

n=0

n=1

n=2

n=0 - максимальное значение

n=1

n=2

n	Число узлов
0	0 (основное)
1	1
2	2

Для осциллятора число узлов волновой функции равно номеру энергетического уровня. Характерное расстояние, на которое волновая функция спадает в раз, называется область локализации функции.

Из рисунка видно, что все волновые функции локализованы вблизи начала координат, при этом самой узкой является волновая функция основного состояния. Она спадает раз при x=x₀. Область от - x₀ до x₀ называется областью локализации. Построим график плотности вероятности при n=0, и на него наложим полную и потенциальную энергии.

При плотность вероятности стремится к нулю. На границе локализации U(x)=E.

Границы области локализации, т.е. точки , это те точки, в которых полная энергия равна потенциальной энергии. В классической механики эти точки называются точками поворота. Согласно классической механике, частица за точками поворота не могла оказаться, т.е. частица колеблется внутри потенциальной ямы от - x₀ до x₀. Согласно квантовой механике вероятность обнаружить частицу за точкой поворота хоть и мала, но отлична от нулю.