ГОС / 42

42. Опыты Штерна-Герлаха, спин электрона. Описание состояния электрона в атоме водорода с помощью квантовых чисел. Спектры излучения атомарного водорода.

Ряд экспериментальных данных указывает на то, что электрон кроме трех степеней свободы поступательного движения (трех координат) обладает еще одной новой степенью свободы, которая может принимать дискретные значения.

Опыт Штерна – Герлаха.

Пучок атомов водорода, находясь в основном состоянии, пропуская через неоднородное магнитное поле. При этом на экране наблюдалось отклонение пучка от первоначального направления в виду расщепления на две симметричные полосы. Так как атомы водорода попадают в магнитное поле в основном состоянии (n=1, l=0).

L будут называть орбитальным моментом импульса, потому что он возникает при придвижении электрона по орбите. С этим орбитальным моментом импульса связан магнитный момент m, следовательно, магнитный момент электрона обусловленным движением электрона, тоже равен нолю. ~

При попадании пучков атома водорода в основном состоянии в магнитное поле, то есть, находясь в - состоянии, расщепление пучка не должно быть. Можно предположить, что эксперимент указывает, что наряду с известным движением электрона (орбитальным), приводящему к отсутствию магнитного момента, имеется «новое движение», которое и обусловливает появление собственного магнитного момента у электрона, находящегося в s- состоянии. Оно и приводит к расщеплению пучка пополам. С собственным магнитным моментом связан собственный механический момент импульса и новое движение электрона вокруг своей оси. Собственный механический вращательный момент импульса электрона называется спином. Другими словами, момент импульса частицы в системе ее покоя, называется спином частицы. Так как при попадании в магнитное поле происходит расщепление пучка атомов водорода пополам, то опыт Штерна – Герлаха указывает на то, что проекция собственного магнитного момента электрона на некоторое выделенное направление (OZ) принимает два значения. То есть проекция спина на OZ так же принимает два значения.

Мультиплетная (сложная) структура атомных спектров.

Пример: атом натрия.

Э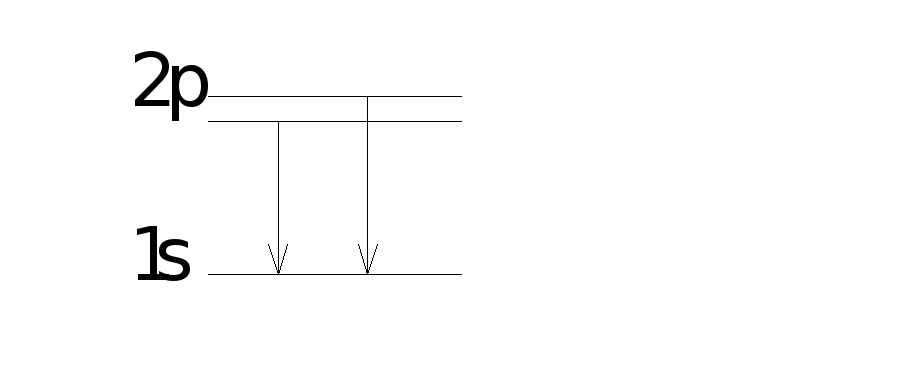кспериментально было обнаружено, что в атоме натрия при переходе из 2p – состояния в 2S –состояние наблюдалась ни одна желтая полоса, а две близлежащие. Если предположить, что полная энергия электрона характеризуется только главным квантовым числом n, то этот эксперимент не понятен.

Рассмотрим подробнее уровень 2p.

Рассмотрим 1S – состояние: n=1, l=0, . В s – состояние орбитальный момент импульса равен нолю, то есть внутреннее магнитное поле, которое расщепляло бы уровень (энергетический) отсутствует. Аналогичная сложная структура наблюдается практически у всех атомов.

Опыт Эйнштейна – де - Гааза (1915).

Ферромагнитный легкий стержень подвешен на тонкой нити и помещен в магнитное поле. При изменении магнитного поля на противоположное, данный стержень механический момент импульса, то есть начинает закручиваться. В данном опыте измерялось отношение изменения магнитного момента к изменению механического момента:

.

Эти измерения были антипараллельны и всегда оказываются пропорциональными друг другу, а именно всегда равняется гиромагнитному отношению.

Если посчитать с классической механики, то появляется коэффициент ½. Если считать с точки зрения квантовой механики и считать, что закручивание стержня обусловливается изменением орбитального момента импульса, то ½ оставалась. Проекция момента импульса измеряется в целочисленных значениях постоянной Планка.

.

Результаты опыта не согласовываются с классическими законами и в тоже время не позволяет считать, что намагниченность ферромагнетика обусловлена не орбитальным движением электрона вокруг своей оси, то есть спином. При этом, если считать, что спин электрона измеряется в полу - целых постоянной Планка, то получится соотношение, согласованное с экспериментом.

~

1. У электрона существует новая степень свободы – собственный вращательный механический момент импульса, то есть спин.

2. Для электрона находящегося в S – состоянии, проекция спина на некоторое выделенное направление может принимать лишь два значения.

3. Значения проекции спина на ось z измеряется в полу – целых постоянной Планка:

(в пренебрежении спин-орбитального взаимодействия).

Рассмотрим квантовую частицу электрон, движущуюся в центрально-симметричном поле неподвижного силового центра и имеющего в этом поле потенциальную энергию:.

Если z=1, то . Это потенциальная энергия взаимодействия электрона с положительно заряженным атомом водорода (с протоном).

Если z=2, то . Это потенциальная энергия взаимодействия с двумя протонами или это есть потенциальная энергия, однонаправленная ионизационная атома гелия.

Если z=3, то - потенциальная энергия взаимодействия с тремя протонами или это есть потенциальная энергия, двукратно ионизационного атома лития.

Во всех этих энергиях можно выделить энергию электрона в атоме водорода, поэтому задача называется водородоподобной.

Водородоподобная задача - это фактически задача об электроне в атоме водорода, а эта есть задача двух тел. Она распадается на две задачи: о движении свободной частицы массы М и о движении частицы с приведенной массой в поле неподвижного силового центра. В качестве массы первой частицы – масса электрона, второй – масса ядра.

(5.1) (5.2)

(5.3)

Так как оператор кинетической энергии представляет собой сумму двух операторов, оператор кинетической энергии поступательного движения, который зависит от и от оператора кинетической энергии вращательного движения, который зависит от , то волновую функцию электрона в поле положительно заряженного ядра можно представить в виде произведения двух функций .

(5,4)

- радиальная функция,- сферическая функция. R зависит от квантовых чисел n и l.

Перепишем (5.4) с учетом (5.3).

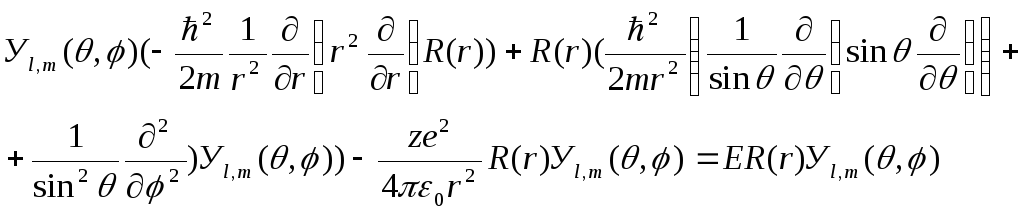(5.5)

(*)

(**)

()

В этом уравнении сферическая функция входит во все слагаемые и является параметром, поэтому на неё сократим.

(5.6)

Решение данного уравнения будем искать в виде:

(5.7)

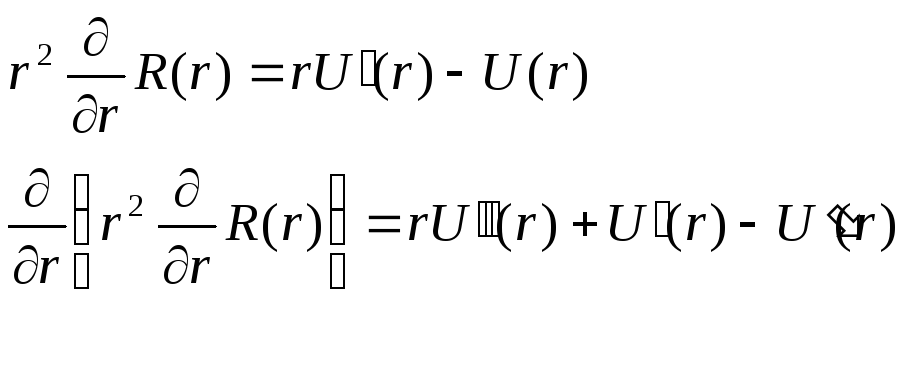
(5.8)

r – Относительное расстояние между электроном и положительно заряженным ядром, .

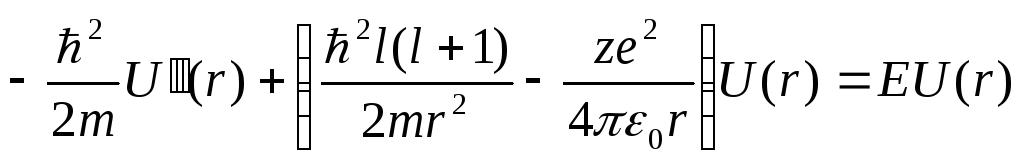
(5.8`)

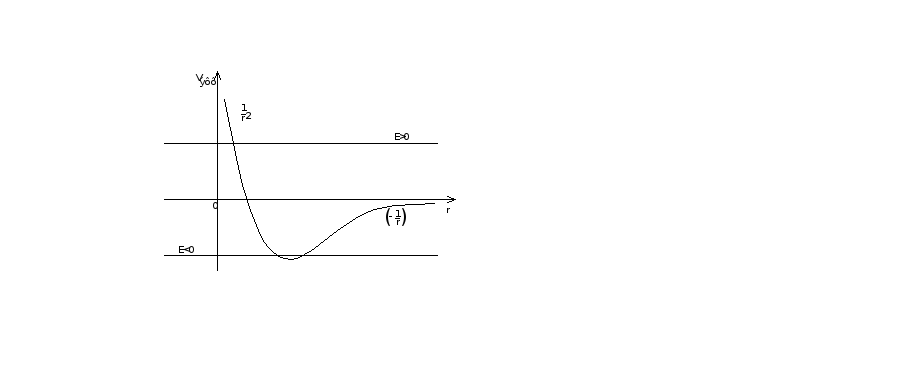
- оператор кинетической энергии.

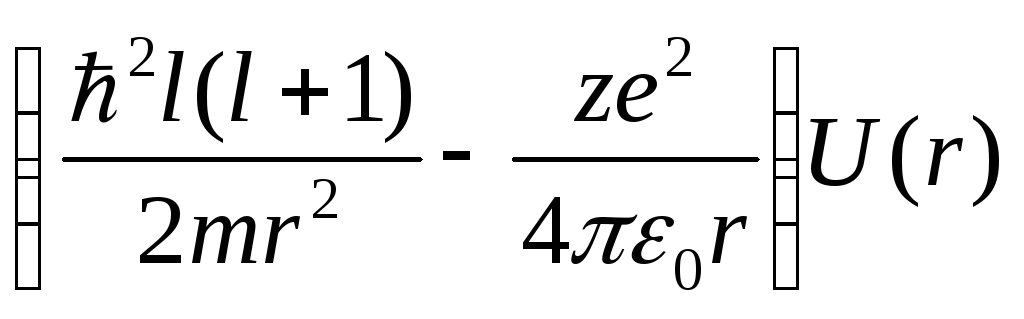- оператор некоторой эффективной потенциальной энергии.

Если Е>0, то это состояние соответствует свободному состоянию электрона, то есть это ионизированное состояние атома. Если Е<0, то это состояние соответствует связанному состоянию электрона. Электрон находится в поле положительного заряженного ядра. Такому состоянию соответствует дискретный спектр значений. Тогда как состояние с Е>0 соответствует непрерывный спектр.

Будем рассматривать связанное состояние электрона. При решении уравнения (5.8) введем новую безразмерную переменную:

(5.10)

a – имеет размерность длинны и равна одному боровскому радиусу.

,

(5.11)

(5.11`)

(5.12)

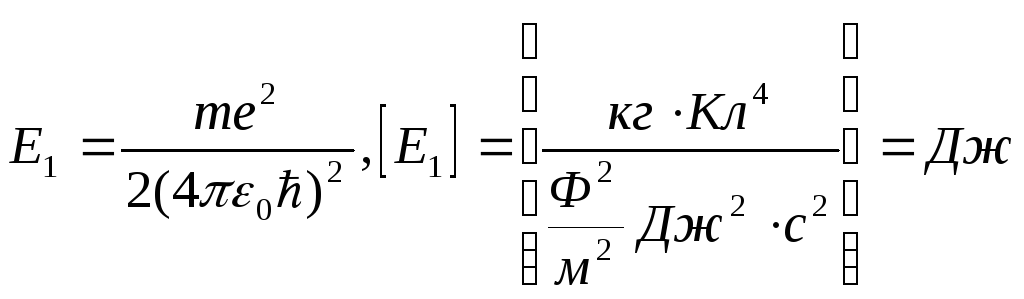
- безразмерная величина.

(5.12`)

(5.12`) будем решать в виде подстановки:

(5.13)

(5.14)

 будем представлять в виде бесконечного ряда:

(5.15)

;

(5.16)

(5.16`)

В первом и третьем слагаемом сдвинем ряд на единицу, это значит, что вместо будет . Объединим первый и третий, второй и четвертый слагаемые.

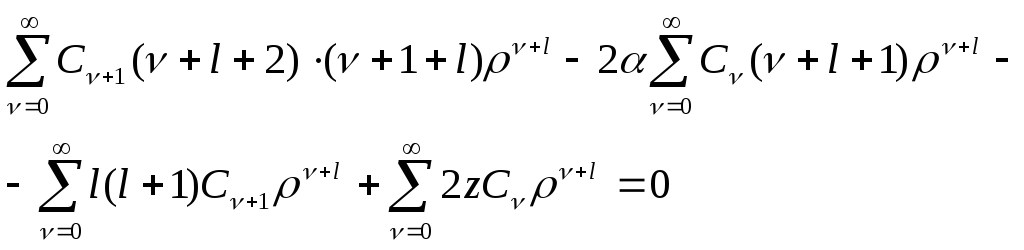
(5.17)

(5.17) говорит о том, что этот бесконечный ряд равен нолю. Чтобы данный ряд был равен нолю необходимо, чтобы коэффициенты ряда, то есть выражение в квадратных скобках, были равны нолю. Из равенства нолю выражения в квадратных скобках получаем связь между коэффициентами ряда:

(5.18)

Данное соотношение между коэффициентами приводит к тому, что выбранная функция в виде бесконечного рада будет стремиться к .

Тогда будет стремиться к и будет стремиться к .

При , . Следовательно, для больших , а значит и R, данное решение уравнения является бессмысленным. Значит необходимо оборвать бесконечный ряд, чтобы получить конечное решение.

Выделим такое, что . Подставим в (5.18):

(5.20)

(5.21)

(5.20`)

(5.22)

(5.22`)

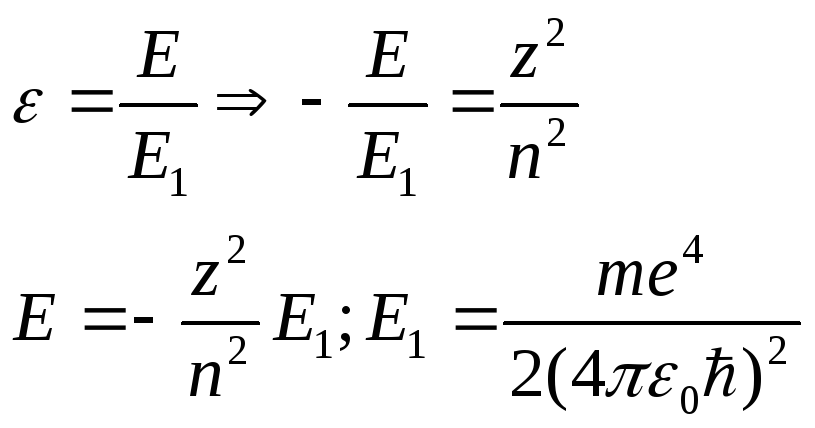
(5.23)

Полная энергия электрона в водородоподобном атоме отрицательна. Полная энергия зависит только от n.

n характеризует полную энергию, называется главным квантовым числом. Тогда Е принимает дискретный ряд значений, или квантуется.

Радиальная часть волновой функции:

(5.24)

Запишем вид радиальной функции через полиномы Лагера, вводя переменную .

(5.25)

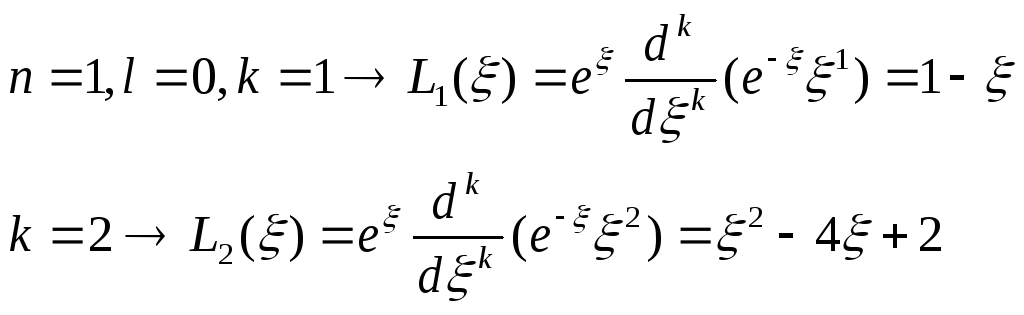
Радиальная составляющая волновой функции определяется квантовыми числами n и l.

; (5.26`)

Полная волновая функция электрона в водородоподобном атоме:

n – главное квантовое число, характеризует полную энергию электрона в водородоподобном атоме. n=1, 2, 3…

l- орбитальное квантовое число, характеризует собственные значения квадрата оператора орбитального момента импульса.

l=0, 1, 2…,n-1

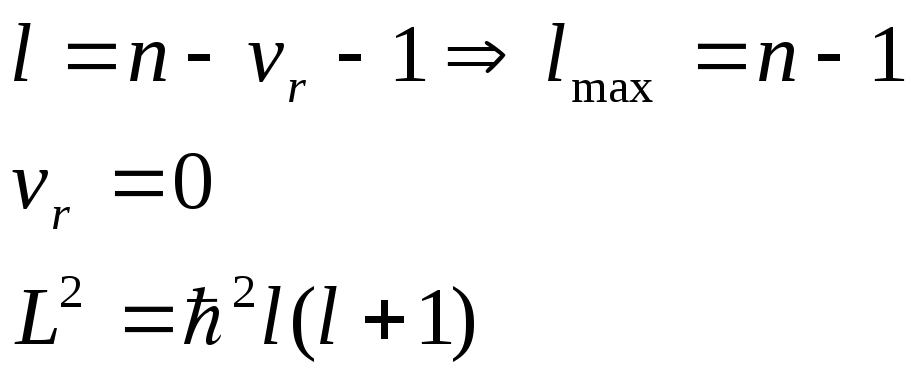
m - магнитное квантовое число. Из теории сферических функций известно, что .

l=-l,…,-1, 0, 1,…, l

При данном значении l, m, принимает (2l+1) значение. m характеризует собственное значение оператора проекции момента импульса на ось z. .

При данном заданном n E принимает одно значение, а волновая функция зависит от n, l, m. Посчитаем, сколько волновых функций принадлежит квантовому энергетическому уровню с энергией (сколько различных квантовых состояний микрочастицы соответствует данному энергетическому уровню). При данном значении n, m принимает (2l+1) значение, а l меняется от 0 до (n+1).

n	Число состояний
1 2 3 4 ...	1 4 9 16 ...

Число различных квантовых состояний (число волновых функций), соответствующих данному значению энергии называется кратностью вырождения данного энергетического уровня. Энергетический уровень, которому соответствуют одно квантовое состояние (одна волновая функция), то такой уровень называется невырожденным.

Совокупность разрешенных энергетических уровней состовлет энергетический спектр.

Рассмотрим полную энергию электрона в атоме водорода. В атоме водорода z=1, тогда

- постоянная Ридберга.

Полная энергия относится как квадраты натуральных чисел.

При переходе электрона со второго, третьего, четвертого и т.д. на первый уровень излучаются кванты света с частотами , который составляет серии линий Лаймона:

(6.1)

При переходе электрона с третьего, четвертого и т.д. уровней на второй излучаются кванты с частотами, которые составляют серию линий Бальмера:

(6.2)

При n=4, 5,… - серии линий Пашина и т.д.

, (6.3)

N – нормировочный множитель.

Полная энергия относится как квадраты натуральных чисел.

При переходе электрона со второго, третьего, четвертого и т.д. на первый уровень излучаются кванты света с частотами , который составляет серии линий Лаймона:

(6.1)

При переходе электрона с третьего, четвертого и т.д. уровней на второй излучаются кванты с частотами, которые составляют серию линий Бальмера:

(6.2)

При n=4, 5,… - серии линий Пашина и т.д.

, (6.3)

N – нормировочный множитель.

Полная энергия относится как квадраты натуральных чисел.

При переходе электрона со второго, третьего, четвертого и т.д. на первый уровень излучаются кванты света с частотами , который составляет серии линий Лаймона:

(6.1)

При переходе электрона с третьего, четвертого и т.д. уровней на второй излучаются кванты с частотами, которые составляют серию линий Бальмера:

(6.2)

При n=4, 5,… - серии линий Пашина и т.д.

, (6.3)

N – нормировочный множитель.

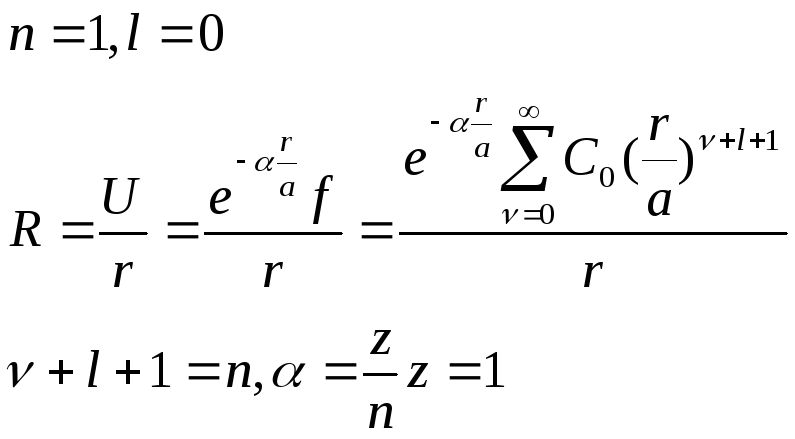
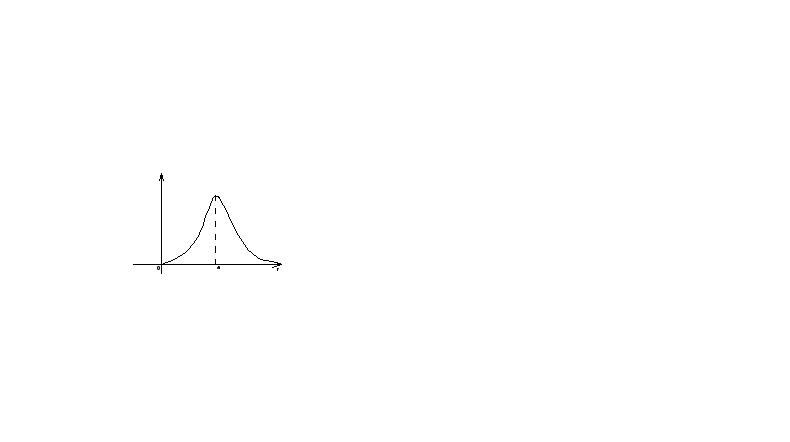
Построим зависимость радиальной плотности вероятности от r.

Основное состояние для электрона в атоме водорода.

Согласно теории Бора, вероятность обнаружить электрон в атоме отлична от ноля только на стационарных орбитах. В частности для основного состояния – это есть первый Боровский радиус. Из теории квантовой механике видно, что вероятность обнаружить электрон в основном состоянии отлична от ноля всюду, где r меняется от 0 до ∞, и максимальна при r=a.

Посчитаем вероятность, или распределение вероятности по углам, при том или ином радиальном распределении. Воспользуемся(6.4`). Проинтегрируем его:

(6.7)

(6.7`)

- элемент телесного угла.

Вероятность обнаружить электрон в атоме водорода в элементе телесного угла при том или ином радиальном распределении.

(6.8)

(*)

Вероятность обнаружить электрон в атоме водорода в единице телесного угла (6.8) не зависит от , то есть не зависит от азимутального угла. Назовем плотностью вероятности и обозначим :

(6.8`)

Зависимо от говорит о том, что в электронной оболочке имеется симметрия вдоль некоторой выделенной оси, а именно оси z. То есть вдоль той оси, где фиксирована проекция момента импульса.

характеризует .

Состояние, в котором орбитальный момент импульса равен нолю, то есть орбитальное квантовое число l принимает нулевое значение, называется S-состоянием.

- S-состояние.

Состояние, в котором орбитальное квантовое число l принимает значение равное единице, называется p-состоянием.