ГОС / 41

41. Принцип тождественности частиц. Свойства симметрии волновых функций относительно перестановки тождественных частиц. Фермионы и бозоны. Принцип Паули.

В природе имеется большое число микрочастиц. Частицы одного сорта обладают разными энергиями, разной скоростью и импульсами, но они имеют одну массу, заряд, спин и т.д. в пределах ошибки измерений. При изучении частиц одного сорта всегда возникал вопрос: “Все ли частицы одинаковы?”

1. Имеется ли в частицах одного сорта хотя бы пара частиц, имеющих различный параметр (хотя бы один).

2. Частицы данного сорта тождественны по всем параметрам.

Многочисленные эксперименты подтвердили именно вторую ситуацию. В эксперименте не нашлось ни одной пары частиц разных хотя бы по одному параметру.

Дадим квантово-механическое описание этого факта:

Рассмотрим систему N – тождественных частиц, тогда

(1)

под обобщенной координатой каждой частицы будем понимать три обычные координаты и спиновую координату

(2)

запишем :

(3)

- оператор кинетической энергии i – й частицы

- оператор потенциальной энергии взаимодействия i – й и k - й частицы

- потенциальная энергия системы частиц во внешнем поле

Оператор полной энергии системы N – тождественных частиц зависит от координат каждой частицы и в общем случае от времени

(3^’)

В квантово-механическом описании мы использовали вторую ситуацию, т.е. считали, что частицы одного сорта обладают одинаковой массой, спином и др. В общем случае положение о тождественности микрочастиц одного сорта можно сформулировать на основе инвариантности гамильтониана относительно перестановки каких-либо двух частиц.

Принцип тождественности:

Если гамильтониан системы частиц не меняется при перестановке любой пары частиц, то данная система частиц тождественна. Аналитически это можно записать следующим образом:

(4)

Введенный признак тождественности микрочастиц на языке гамильтониана отражается па свойствах волновой функции, описывающих состояние микрочастиц. Введем оператор перестановки двух частиц:

- переставляет i – ю и k – ю частицы

(5)

Подействуем оператором перестановки дважды на волновую функцию:

в результате получили ту же самую волновую функцию, т.е.

- собственная функция оператора квадрата перестановки

1(единица) – собственное значение оператора квадрата перестановки (6)

(7)

подействуем справа оператором перестановки еще раз:

- число, которое можно вносить и выносить из оператора перестановки

используя (7), получим

(8)

- собственное значение оператора квадрата перестановки

из (6) видно, что (9)

тогда (10)

1.

(11)

видим, что волновая функция получается симметричной относительно перестановки двух частиц.

Частицы, волновая функция которых не меняет знак при перестановке любой пары частиц, называются бозе-частицами.

2.

(12)

получили антисимметричную волновую функцию.

Частицы, волновая функция которых меняет знак при перестановке любой пары частиц, называются ферми-частицами.

Т.к. возможны два собственных значения оператора перестановки, в природе возможны частицы двух сортов. Их назвали бозе- и ферми-частицами.

Существует теорема о связи спина со статистикой частицы. Из этой теоремы следует:

Бозе-частицы являются частицами с целочисленным спином. Это значит, что спин частицы может быть равен 0 или кратен постоянной Планка (S=0, S=).

Пример бозе-частиц: фотоны, фононы, - мезоны.

Ферми-частицами обладают полуцелым спином ()

Пример ферми-частиц: электроны, протоны, нейтроны, Σ-гиперон ().

Принцип Паули был сформулирован в квантовой механике на основе спектроскопических данных. Первая формулировка принципа Паули:

В одном состоянии не может находиться более одного электрона (частицы).

Если будем рассматривать электрон в связном состоянии, то волновая функция характеризуется n, l, m, m_s:

n = 1, 2 …

l =

m =

m_s =

В свободном состоянии:

Принцип Паули можно сформулировать следующим образом:

В одном квантовом состоянии не может быть двух или более электронов, описываемых одним и тем же набором квантовых чисел.

Данный принцип позволяет качественно правильно объяснить заполняемость атомных оболочек электронами, т.е. понять строение атомов и распределение электронов в таблице Менделеева.

Однако, данная формулировка несколько упрощена, т.к. с точки зрения квантовой механики непонятно как в системе большого числа электронов рассматривать квантовое состояние, соответствующее одному электрону. Также непонятно, как в это состояние (состояние одного электрона) помещать другой электрон. При этом образуется двухэлектронная система и первоначальное состояние электрона должно измениться за счет межэлектронного взаимодействия. Можно освободиться от этих неясностей, дав третью формулировку:

Знаем, что электроны - ферми-частицы. Можно производить процесс измерения квантовых чисел. Это значит, что при измерении квантового числа n мы измеряем полную энергию, при измерении квантового числа l измеряем квадрат орбитального момента импульса, при измерении m – проекцию момента импульса, а при измерении m_s – проекцию спина. А для свободного электрона будем измерять три квантовых числа и .

В системе из одинаковых ферми-частиц в результате измерения полного набора квантовых чисел не может быть получено два и более одинаковых набора, относящихся к отдельным ферми-частицам в один и тот же момент времени.

Докажем принцип Паули:

Будем доказывать для системы двух ферми-частиц:

В результате измерения полного набора квантовых чисел у первого электрона, получим волновую функцию

- в связном состоянии,

- в свободном состоянии,

- в связном состоянии,

- в свободном состоянии.

В результате измерения полного набора квантовых чисел у второго электрона, получим волновую функцию

, - волновые функции, соответствующего оператора полной энергии, т.е. составляют систему ортонормированных функций или полную систему ортогональных функций.

Поэтому систему функций двух ферми-частиц можем представить как суперпозицию ортогональных функций, т.е. разложить в ряд по полной системе ортогональных функций:

(1)

- волновая функция системы двух ферми-частиц, а волновые функции ферми-частиц антисимметричны.

(2)

(3)

в этом разложении - коэффициенты разложения, а - вероятность обнаружить первую частицу в состоянии n₁ , вторую частицу – в состоянии n₂

Под n₁ для связного состояния понимаем .

Под n₂ также понимаем . Т.е. спектр дозволенных значений квантовых чисел первой частицы совпадает со спектром дозволенных значений второй частицы. А т.к. суммы n₁ и n₂ пробегают один и тот же ряд значений, то индексы суммирования можно менять местами. Это значит, что

(3’)

(4)

Рассмотрим случай, когда n₁= n₂= n, тогда

(5)

Следовательно, вероятность обнаружить два одинаковых набора квантовых чисел при измерении двух наборов квантовых чисел равна нулю. Такое событие невозможно, т.е. принцип Паули доказан.

1. Построение волновых функций системы ферми-частиц.

Рассмотрим две ферми-частицы: состояние первой частицы описывается волновой функцией , второй частицы - .

Эти волновые функции являются собственными волновыми функциями соответствующих операторов полной энергии и составляют полную систему ортогональных функций, тогда волновую функцию системы двух ферми-частиц можем представить как суперпозицию ортогональных функций, т.е. разложить в ряд по полной системе ортогональных функций:

рассмотрим сумму по n₁ и получим две суммы: по n₁ > n₂ и n₁ < n₂ (n₁ и n₂ пробегают один и тот же ряд значений, следовательно их можно поменять местами)

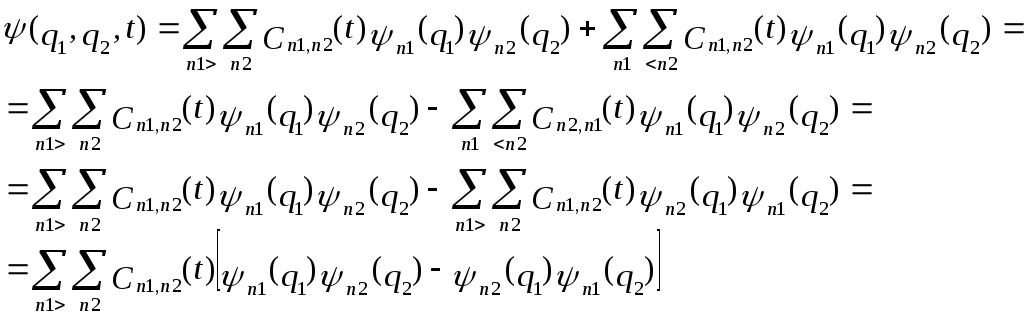
(1)

Данное выражение говорит о том, что в состоянии n₁ может находиться первая частица, а в состоянии n₂ – вторая. Однако, может быть и наоборот.

Если мы возьмем квадрат модуля этого выражения, то интеграл от квадрата модуля первого слагаемого будет численно равен интегралу от квадрата модуля второго слагаемого. При интегрировании будут возникать перекрестные слагаемые.

(1’)

(2)

При решении конкретных физических задач с хорошей точностью можно считать, что если первая частица находится в квантовом состоянии, характеризующемся набором n₁, то при помещении в это состояние частицы, характеризующейся набором квантовых чисел n₂, состояние первой частицы не изменится, т.е. в системе двух ферми-частиц не учитывается случай взаимодействия этих частиц между собой.

(3)

2. Построение волновых функций системы бозе-частиц

Рассмотрим две бозе-частицы:

состояние первой частицы описывается волновой функцией , второй частицы - . Эти волновые функции ортонормированны:

(4)

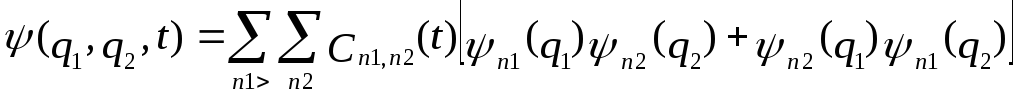(5)

А если не учитывать взаимодействие бозе-частиц между собой, то

(6)