40 Одномерное движение квантовой частицы: свободный электрон, электрон в потенциальной яме, одномерный квантовый осциллятор. Туннельный эффект.

Рассмотрим случай, когда на пути частицы в пространстве в каком-то одном направлении имеется так называемая потенциальная яма, т.е. когда потенциальная энергия вдоль оси имеет вид:

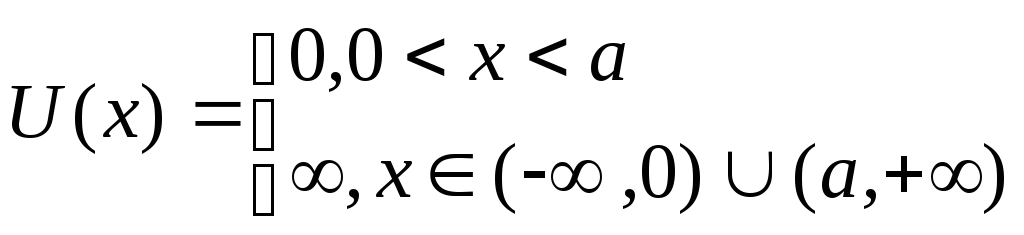
, - ширина ямы.

Предположим, что частица находится внутри такой потенциальной ямы.

Чтобы решить задачу, надо решить стационарное уравнение Шредингера, т.е. надо найти полную энергию частицы и её волновую функцию.

(6.1)

(6.2)

Волновую функцию можно представить в виде произведения двух функций:

(6.3)

Подставим (6.3) в (6.1) с учетом (6.2):

(6.4)

(6.4) - одномерное уравнение Шредингера.

(6.4')

Частица находится в яме; стенки ямы бесконечны. За бесконечную стенку частица выйти не может. Следовательно, вне ямы частицы нет и волновая функция вне ямы равна нулю.

1. ,

2. Частица в яме:

,

(6.5)

(6.5')

(6.6)

Частица в яме обладает только кинетической энергией, >0.

(6.7)

(6.7) – однородное дифференциальное уравнение второго порядка с постоянным коэффициентом. Решением представим в тригонометрическом виде:

(6.8)

Чтобы найти и , применим граничные условия. Мы знаем, что волновая функция должна быть непрерывной на границах ямы. Т.к. вне ямы волновая функция равна нулю, то, в силу непрерывности, она равна нулю и на границах ямы.

1) 2)

,

,

меняется дискретно и зависит от , но .

Зная , мы можем определить полную энергию.

, (6.11)

Полная энергия меняется в зависимости от , следовательно, она квантуется и принимает дискретный ряд значений.

Применим условие нормировки для волновой функции:

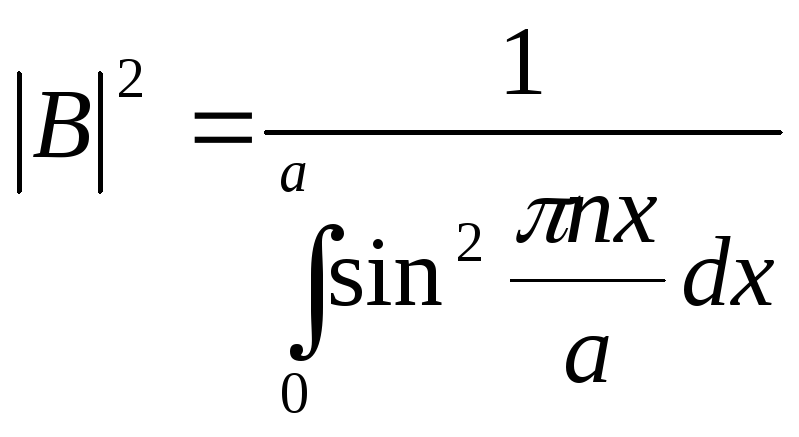
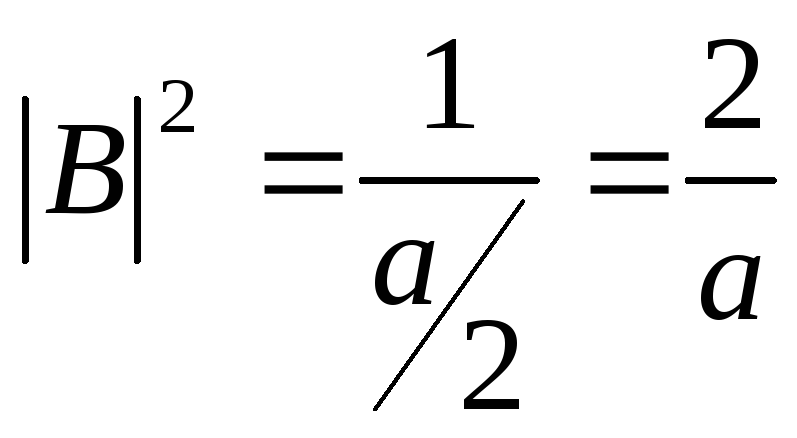
(6.12)

- номер энергетического уровня, главное квантовое число.

Построим волновые функции и плотность вероятности.

;

;

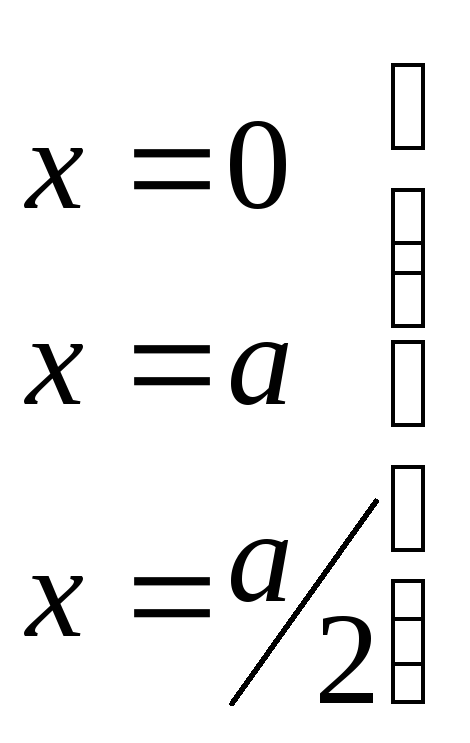
Плотность вероятности волновой функции:

Точка, в которой волновая функция обращается в ноль, не считая граничных, называется узлом.

Число узлов волновой функции на единицу меньше номера энергетического уровня.

Состояние, в котором волновая функция не имеет узлов, называется основным, или низшим. Следовательно, состояние частицы в яме при основное, или низшее.

Построим зависимость энергии от главного квантового числа .

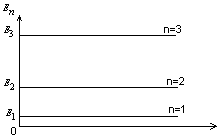
-полные энергии частицы в яме относятся как квадраты натуральных чисел.

(6.13)

(6.13) – для микрочастиц энергетическая разность является существенной, т.к. разность между энергетическими уравнениями определяется массой частицы, шириной ямы и главным квантовым числом. Если же рассматривать макрообъекты, то эта разность стремится к нулю, т.е. эти расстояния ничтожно малы и для макротел не учитываются.

Пример потенциальной ямы.

Предположим, что нам необходимо удалить электрон из металла. Можно предположить, что свободный электрон в металле обладает потенциальной энергией равной нулю. Чтобы электрон вышел из металла, ему необходимо преодолеть потенциальную энергию , т.е. фактически можно считать, что электрон в металле находится в потенциальной яме, высота которой равна .

Рассмотрим случай, когда частица движется в поле потенциальных сил, обращающихся в ноль на бесконечности и имеющих в некоторой характерной области некоторое положительное значение.

Пусть частица попадает в такое поле.

Классический подход:

1. - частица отразится.

2. - частица пройдет.

С точки зрения квантовой механики, свободная частица описывается волновой функцией, и эта функция есть волна де Бройля. Как известно, волны могут испытывать отражения от препятствий, а могут огибать их, или дифрагировать, т.е. частицы могут проникать за пределы барьера даже с энергией меньшей высоты этого барьера. Могут и отражаться от барьера с энергией больше высоты барьера.

Потенциальный барьер произвольной формы всегда можно представить в виде совокупности прямоугольных барьеров, состыкованных между собой. Вероятность прохождения частицы через барьер произвольной формы равна произведению вероятностей прохождения частицы через каждый прямоугольный барьер.

Рассмотрим простейший потенциальный барьер прямоугольной формы.

,

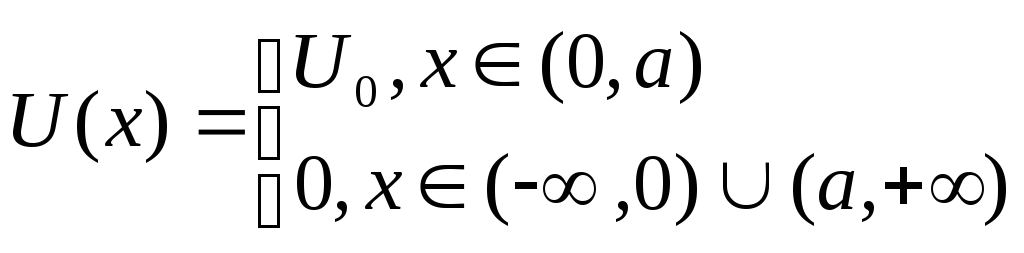
- высота прямоугольного барьера,

- ширина прямоугольного барьера.

Запишем уравнение Шредингера для одномерного случая:

(7.1)

Барьер разбивает пространство вдоль оси на три области.

I.

(7.2)

(7.2')

(7.3)

(7.4)

II.

(7.5)

(7.5')

(7.6)

(7.7)

Знак зависит от знака .

Рассмотрим случай .

1) , , - действительное.

(7.8)

2) , , - мнимое, (*)

(7.9)

Решение второй области во втором случае представляет собой позицию экспоненциально возрастающего и экспоненциально спадающего решения. Но т.к. область ограничена, то такое решение возможно и отлично от нуля.

III.

Аналогично случаю I, получим

(7.11)

(7.12)

При этом предположим, что полная потенциальная энергия частицы при прохождении через потенциальный барьер сохраняется.

Неизвестны коэффициенты . Для их определения, необходимо применить граничные условия:

1. Волновая функция на границах барьера должна быть непрерывна.

1) 2)

2. Непрерывна на границах барьера должна быть и первая производная от волновой функции, т.к. потенциальная энергия не испытывает бесконечного скачка.

3) 4)

Чтобы получить полное решение уравнения Шредингера, необходимо домножить на временную часть: (**)

Первое слагаемое в правой части – это плоская монохроматическая волна, распространяющаяся в положительном направлении оси , т.е. падающая на барьер волна. - амплитуда волны, падающей на барьер.

Второе слагаемое представляет собой волну, распространяющуюся в отрицательном направлении оси , т.е. это отраженная от барьера волна.

Первое слагаемое в правой части – это плоская монохроматическая волна, прошедшая над барьером.

Второе слагаемое представляет собой волну, отраженную над барьером.

Следовательно, можно обнаружить частицу внутри барьера.

Первое слагаемое – это плоская монохроматическая волна, прошедшая через барьер.

Второе слагаемое представляет собой отраженную волну. Амплитуда отраженной волны .

В третьей области отражаться не от чего. Следовательно, волны не существует.

I.

1)

(7.13)

2) (7.14)

II. 3)

(7.15)

4)

(7.16)

Условие нормировки:

Если учесть, что - амплитуда падающей волны, то можно предположить, что

(7.17)

Коэффициент в I и III областях одинаков.

(7.18)

(7.19)