
ГОС / 25
.doc25. Вынужденные колебания линейного гармонического осциллятора в отсутствии и при наличии сил трения. Явление резонанса. Автоколебания.
Вынужденные колебания при гармоническом внешнем воздействии.
В том случае, когда на колебательную систему оказывается периодическое внешнее воздействие, подчиняющееся гармоническому закону, колебания описываются уравнением вида:
С учетом
трения:

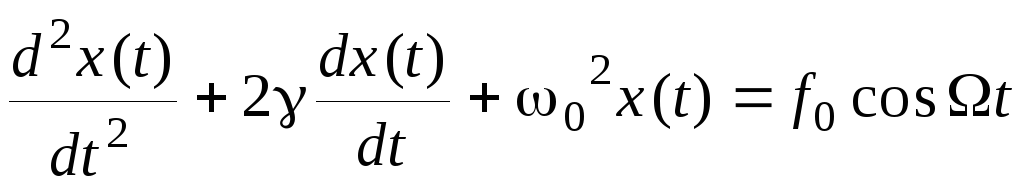 ,
(1) где
,
(1) где
![]() - коэффициент затухания,
- коэффициент затухания,
![]() - собственная частота системы, т.е.
частота, с которой совершались бы
колебания в отсутствии затухания,
- собственная частота системы, т.е.
частота, с которой совершались бы
колебания в отсутствии затухания,
![]() -
частота
вынуждающего воздействия на систему.
-
частота
вынуждающего воздействия на систему.
В
Рис.2. Колебательный
контур с вынуждающим воздействием
Рис.1. Пружинный
маятник
с вынуждающей
силой
![]() зависит от вида колебательной системы
и внешнего воздействия. Например, для
пружинного маятника
зависит от вида колебательной системы
и внешнего воздействия. Например, для
пружинного маятника
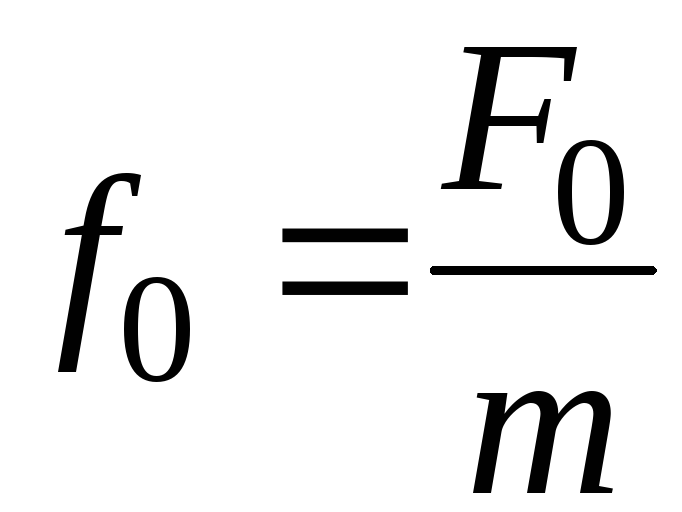 ,
где
,
где
![]() - амплитуда вынуждающей
силы (рис
1). Для вынужденных колебаний в колебательном
контуре:
- амплитуда вынуждающей
силы (рис
1). Для вынужденных колебаний в колебательном
контуре:
 ,
где
,
где
![]() - амплитуда переменного напряжения,
подаваемого на колебательный контур,
- амплитуда переменного напряжения,
подаваемого на колебательный контур,
![]() - индуктивность (рис 2). Общее решение
такого неоднородного дифференциального
уравнения (1) равно сумме общего решения
соответствующего однородного уравнения
и частного решения неоднородного
уравнения. Эти два слагаемых соответствуют
свободным затухающим колебаниям и
незатухающим колебаниям с частотой
вынуждающей силы. По истечении некоторого
промежутка времени решение уравнения
(1) будет совпадать с частным решением.
- индуктивность (рис 2). Общее решение
такого неоднородного дифференциального
уравнения (1) равно сумме общего решения
соответствующего однородного уравнения
и частного решения неоднородного
уравнения. Эти два слагаемых соответствуют
свободным затухающим колебаниям и
незатухающим колебаниям с частотой
вынуждающей силы. По истечении некоторого
промежутка времени решение уравнения
(1) будет совпадать с частным решением.
Описываемый им режим движения называется установившимся режимом вынужденных колебаний. Соответствующее выражение имеет вид
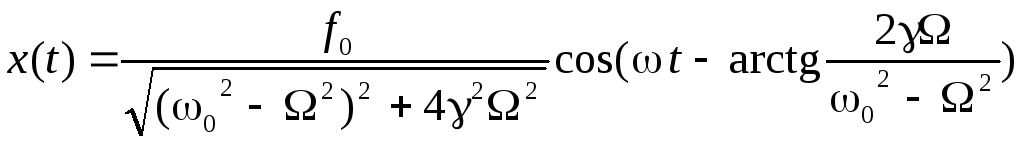 .
(2)
.
(2)
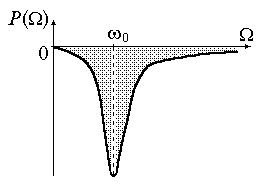
Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы:
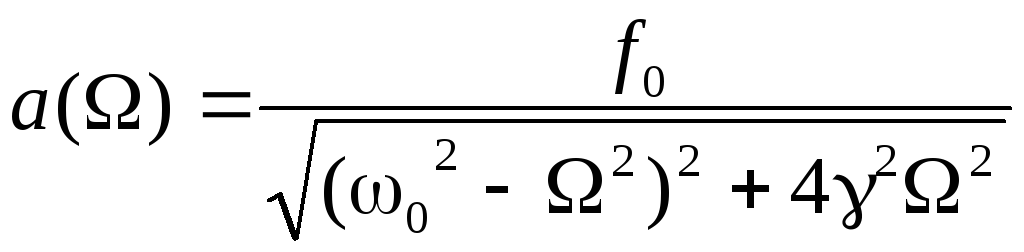 .
(3)
.
(3)
Величина
 (4)
(4)
характеризует
отставание по фазе вынужденного колебания
от обусловившего это колебание внешнего
воздействия. Следует отметить, что
установившиеся колебания происходят
с частотой вынуждающего воздействия
W,
а не с собственной частотой. При W
= 0 выражение (3) дает статическое отклонение
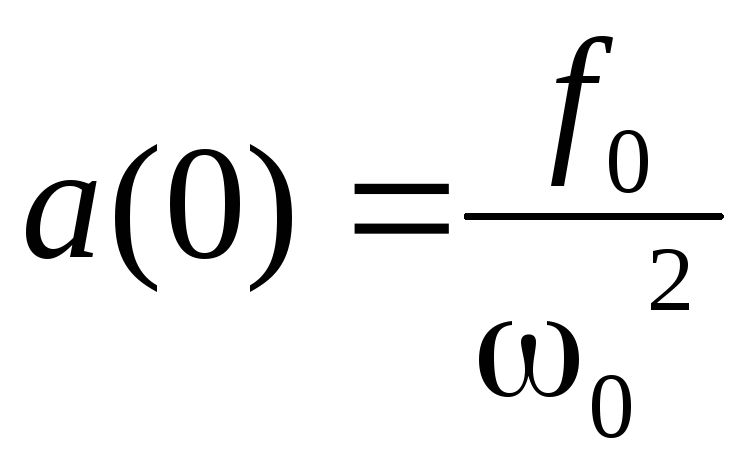 .
(5)
.
(5)
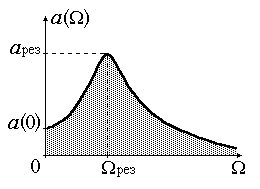
Зависимость
амплитуды вынужденных колебаний от
частоты вынуждающего воздействия (рис.
3) приводит к тому, что при некоторой
определенной для данной колебательной
системы частоте амплитуда колебаний
достигает максимального значения.
Резкое возрастание амплитуды вынужденных
колебаний при приближении частоты
внешнего воздействия к некоторому
значению называют явлением резонанса
(резонансом).
Резонансную
частоту
![]() находят, приравнивая нулю производную
находят, приравнивая нулю производную
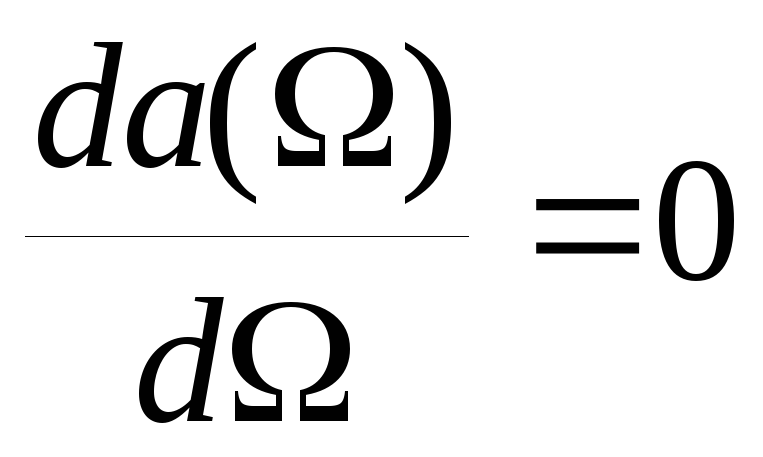 ,
откуда
,
откуда
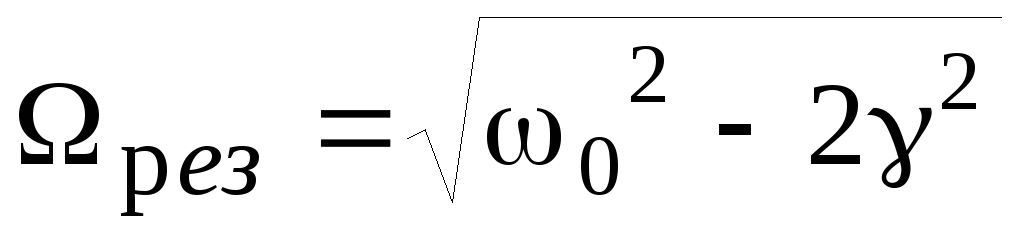 (6)
(6)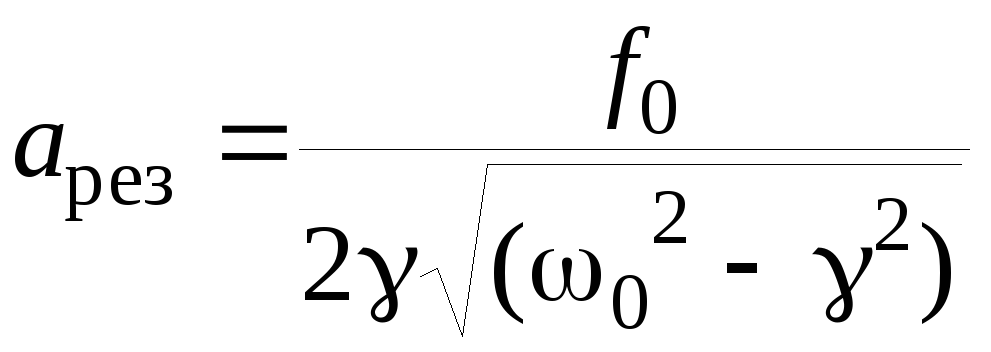 .
(7)
.
(7)
|
Рис.3. Резонансная кривая |
 ля
механических колебаний при резонансной
частоте внешнего воздействия, определяемой
по формуле (6), достигается максимум
амплитуды смещения колеблющейся величины
ля
механических колебаний при резонансной
частоте внешнего воздействия, определяемой
по формуле (6), достигается максимум
амплитуды смещения колеблющейся величины
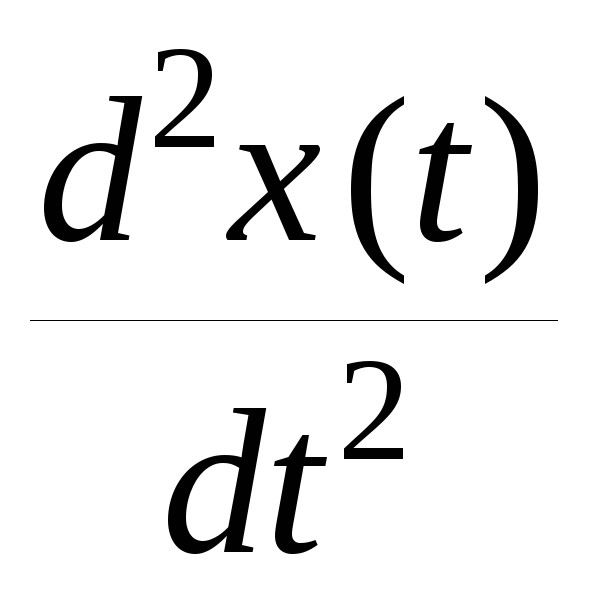 (соответственно, ускорения или напряжения
на катушке индуктивности) достигается
при
(соответственно, ускорения или напряжения
на катушке индуктивности) достигается
при
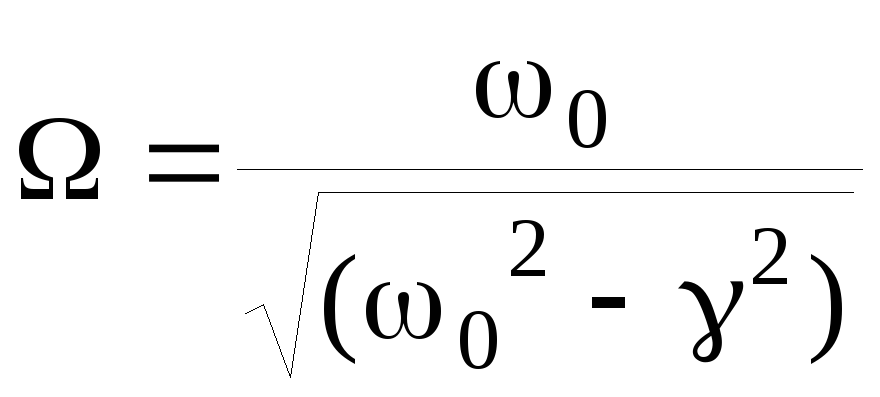 .
Максимум средней мощности внешнего
воздействия (для механических колебаний
максимум мощности внешней силы
.
Максимум средней мощности внешнего
воздействия (для механических колебаний
максимум мощности внешней силы
 )
достигается при
)
достигается при

 .
(8)
.
(8)
В
![]() называется резонансной
кривой (см. рис.3.).
называется резонансной
кривой (см. рис.3.).
В установившемся режиме вынужденных колебаний энергия колебательной системы остается неизменной. Система непрерывно поглощает от источника внешнего воздействия энергию, которая восполняет потери, связанные с наличием затухания (сила трения при механических колебаниях, выделение теплоты на активном сопротивлении при колебаниях в контуре).
Найдем среднюю энергию, поглощаемую в единицу времени. Вычисления проведем для пружинного маятника при наличии силы трения и периодически изменяющейся внешней силы. При смещении груза на dx внешняя сила совершит работу Fdx.
Работа,
совершенная в единицу времени, будет
равна
![]() .
Среднее значение поглощаемой в единицу
времени энергии равно:
.
Среднее значение поглощаемой в единицу
времени энергии равно:
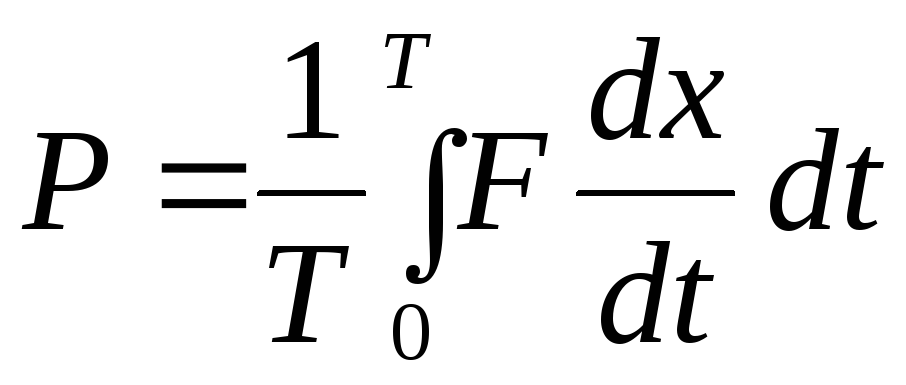 .
(9)
.
(9)
Здесь
усреднение производится по одному
периоду колебаний
 .
Подставляя в интеграл (9) выражение для
силы,
.
Подставляя в интеграл (9) выражение для
силы,
![]() и производную от смещения
и производную от смещения
![]() из выражения (2), получаем
из выражения (2), получаем
 , (10)
, (10)
где величина j определяется выражением (4). После интегрирования находим:
![]() . (11)
. (11)
Преобразование
![]() с учетом (4) приводит к выражению:
с учетом (4) приводит к выражению:
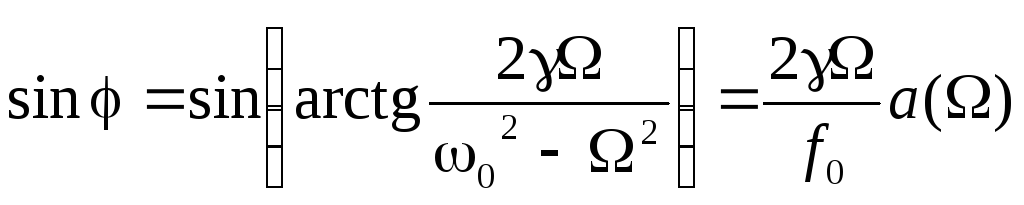
 . (7.3.12)
. (7.3.12)
Учитывая,
что
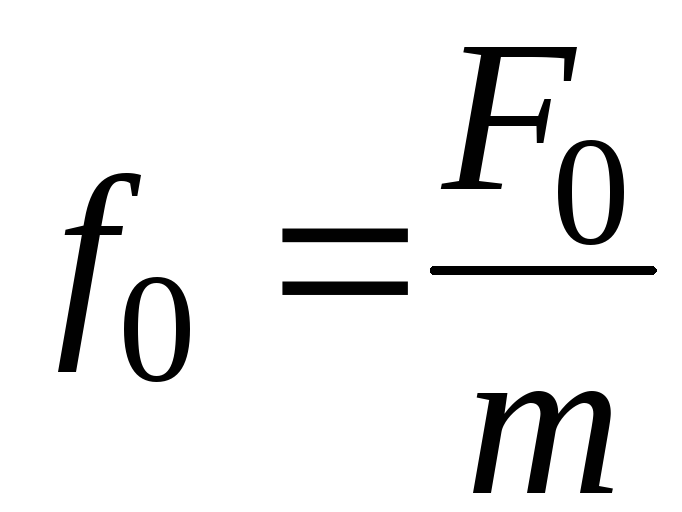 ,
получаем:
,
получаем:
![]() . (7.3.13)
. (7.3.13)
К
Рис. 4. Зависимость
поглощенной энергии от частоты
![]() зависит от частоты W.
Так как
зависит от частоты W.
Так как
![]() имеет резонансный пик – максимум, то
имеет резонансный пик – максимум, то
![]() имеет резонансный пик – минимум (см.
рис. 4) Поэтому измерения зависимости
поглощенной энергии от частоты позволяют
обнаружить резонансные явления и
установить собственные частоты
осциллирующих систем.
имеет резонансный пик – минимум (см.
рис. 4) Поэтому измерения зависимости
поглощенной энергии от частоты позволяют
обнаружить резонансные явления и
установить собственные частоты
осциллирующих систем.
без учета трения:
![]() ,
(2.1)
,
(2.1)
![]() ,
(2.2), где
,
(2.2), где
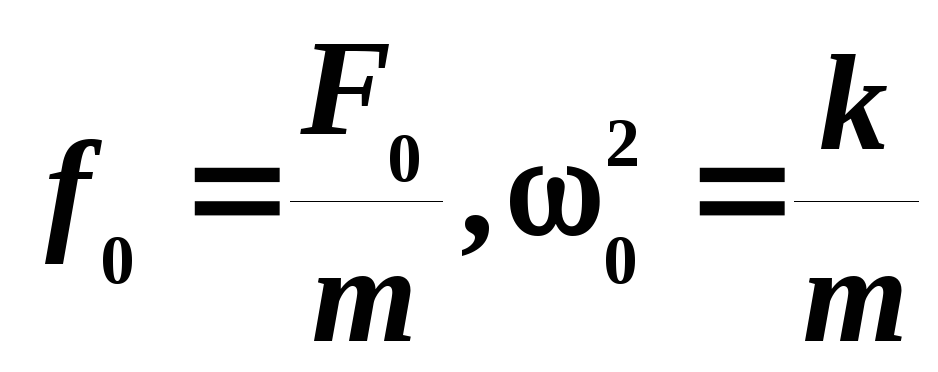 .
Найдем частное решение неоднородного
уравнения. Решение будем искать в виде
.
Найдем частное решение неоднородного
уравнения. Решение будем искать в виде
![]() .
Подставив
.
Подставив
![]() в
уравнение (2.2) получим уравнение для
в
уравнение (2.2) получим уравнение для
![]() :
:![]() .
Откуда
.
Откуда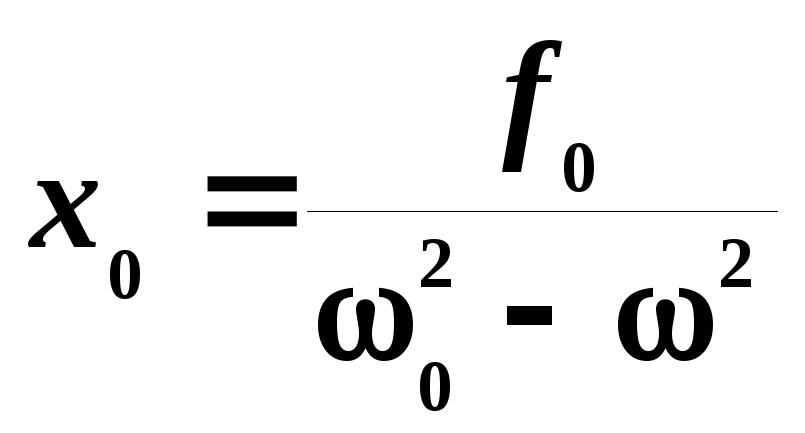 .
.
Общее решение
однородной части уравнения является
линеиной комбинацией
![]() и
и
![]() .
Зная общее решение однородной части
уравнения и частное решение можно
составить общее решение неоднородного
уравнения (3.2):
.
Зная общее решение однородной части
уравнения и частное решение можно
составить общее решение неоднородного
уравнения (3.2):
 .
.
Раскачка из состояния покоя.
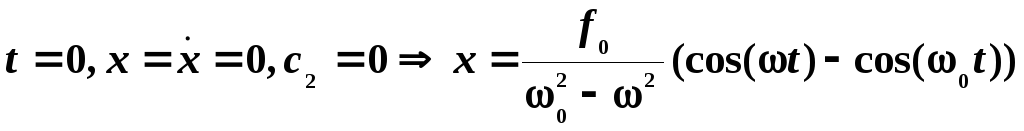
![]()
Пусть
![]() .
.
![]()
![]()
![]()
![]() -резонансный
член, возникает неограниченный рост
амплитуды.
-резонансный
член, возникает неограниченный рост
амплитуды.
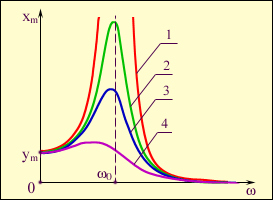
Резонансные
кривые при различных уровнях затухания.
1
- колебательная система без трения; при
резонансе амплитуда xm
вынужденных колебаний неограниченно
возрастает; 2, 3, 4 - реальные резонансные
кривые для колебательных систем с
различной силой трения: Fтр4>Fтр3>Fтр2.
На низких частотах (![]() )
)
![]() .
На высоких частотах (
.
На высоких частотах (![]() )
)
![]() .
.
Автоколебания, незатухающие колебания, которые могут существовать в какой-либо системе при отсутствии переменного внешнего воздействия, причём амплитуда и период колебаний определяются свойствами самой системы. Этим автоколебания отличаются от вынужденных колебаний, амплитуда и период которых определяются характером внешнего воздействия (приставка «авто» и указывает на то, что колебания возникают в самой системе, а не навязываются внешним воздействием). Автоколебания отличаются и от свободных колебаний (например, колебаний свободно подвешенного маятника, колебаний силы тока в электрическом контуре) тем, что, во-первых, свободные колебания постепенно затухают, во-вторых, их амплитуда зависит от первоначального «толчка», создающего эти колебания. Примерами автоколебания могут служить колебания, совершаемые маятником часов, колебания струны в смычковых или столба воздуха в духовых музыкальных инструментах, электрические колебания в ламповом генераторе. Системы, в которых возникают автоколебания, называются автоколебательными. Автоколебательные системы во многих случаях можно разделить на 3 основных элемента: 1) колебательную систему (в узком смысле); 2) источник энергии, за счет которого поддерживаются А., и 3) устройство, регулирующее поступление энергии из источника в колебательную систему. Эти 3 основных элемента могут быть отчётливо выделены, например, в часах, в которых маятник или баланс служит колебательной системой, пружинный или гиревой завод — источником энергии, и, наконец, анкерный ход — механизмом, регулирующим поступление энергии из источника в систему. В часах, например, автоколебания осуществляются следующим образом (рис.). При прохождении качающегося балансира 1 через определённое положение (обычно дважды за период) спусковое устройство 2 и 3 подталкивает колесо балансира, сообщая ему энергию, необходимую для того, чтобы компенсировать потерю энергии за полпериода колебаний. Балансир часов совершает автоколебания с амплитудой, целиком определяемой свойствами часового механизма. Однако для того, чтобы эти автоколебания возникли, обычно нужно не только завести пружинный завод, но и слегка встряхнуть часы, т. е. сообщить начальный толчок балансиру. Т. о., часы — это в большинстве случаев автоколебательная система без самовозбуждения. В духовых инструментах продувание струи воздуха поддерживает автоколебания столба воздуха в трубе инструмента, а в струнных смычковых инструментах автоколебания поддерживаются силой трения, действующей между смычком и струной.

Спусковой механизм часов: 1 — балансир; 2 — анкерная вилка; 3 — спусковое колесо.
