ГОС / 20

20. Закон Био-Савара-Лапласа, его применение к расчету магнитных полей. Закон электромагнитной индукции. Опыты Фарадея.

Начать с 3 ур максв кот…. (предыд вопр)

Рассмотрим объем, в котором текут постоянные токи. Необходимо определить вектор индукции магнитного поля, создаваемого этими токами в любой точке пространства вне этого объема, например, в точке М.

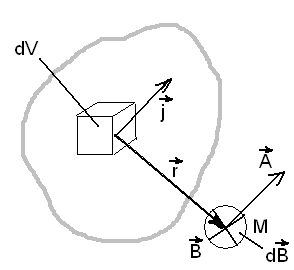
Радиус- вектор, проведенный в точку M, и будет радиус- вектором в (7.7). .

(7.8)

Согласно (7.1), операция rot (7.8) берется по координатам точки наблюдения, а интегрирование ведется по координатам объема.

Операция rot берется по координатам точки наблюдения, а вектор зависит от координат элемента объема, поэтому относительно ротора вектор считается постоянным и равен .

(7.11)

(7.10)

(7.11)- и есть закон Био-Савара-Лапласа для объемных токов.

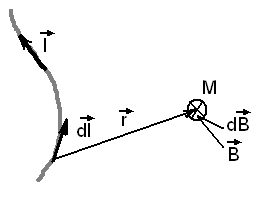
Определим направление :

(7.11’).

- вектор индукции магнитного поля, создаваемый в точке элементом объемного тока .

Направление вектора определяется правилом правого винта или буравчика: если смотреть навстречу вектору , то вращение от вектора к вектору должно происходить против часовой стрелки.

, отсюда следует, что лежит в плоскости, перпендикулярной плоскости чертежа.

Получим закон Био-Савара-Лапласа для линейных токов.

В большинстве практически важных случаев постоянные токи текут по достаточно тонким проводникам, распределяясь с равномерной плотностью по поперечному сечению этих проводов. Такие токи называются линейными.

Тонким считается провод, линейные размеры поперечного сечения которого много меньше расстояний до точек, в которых вычисляется поле.

Рассмотрим элемент длины линейного проводника, площадь поперечного сечения которого равна S:

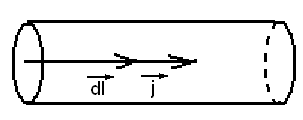
Кроме того, объемный интеграл переведем в линейный и если линейный проводник замкнутый, то и интеграл замкнутый.

(7.12)

Если рассматриваемая цепь не содержит разветвлений, то по ней течет постоянный ток, в (7.12) его можно вынести за знак интеграла, тогда получим:

Определим направление вектора :

Пример:

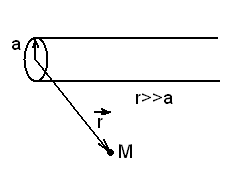
Вычислим магнитное поле, создаваемое бесконечно длинным прямым тонким проводом (вектор индукции или напряженности в любой точке вне проводника). Выберем произвольную точку M, находящуюся на расстоянии a от данного проводника.

Воспользуемся (7.12’) для проводников, тогда определяется выражением (7.13). Выберем и проведем .

Удобнее от интегрирования по длине перейти к интегрированию по углу . При этом .

AO обозначим –l, тогда .

. Продифференцируем: .

Проинтергируем по от 0 до :

, где - кратчайшее расстояние от точки наблюдения до провода с током представляет собой концентрические окружности:

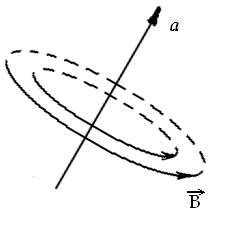
Закон: При изменении потока магнитной индукции через поверхность, ограниченную замкнутым проводником, в нём возникает электрический ток под действием электродвижущей силы индукции. ЭДС индукции, возникающая в замкнутом проводнике, по которому течёт ток, определяется скоростью изменения(уменьшения) магнитного потока, пронизывающего контур.

(7.1)

- работа электрических сил по перемещению единичного заряда.

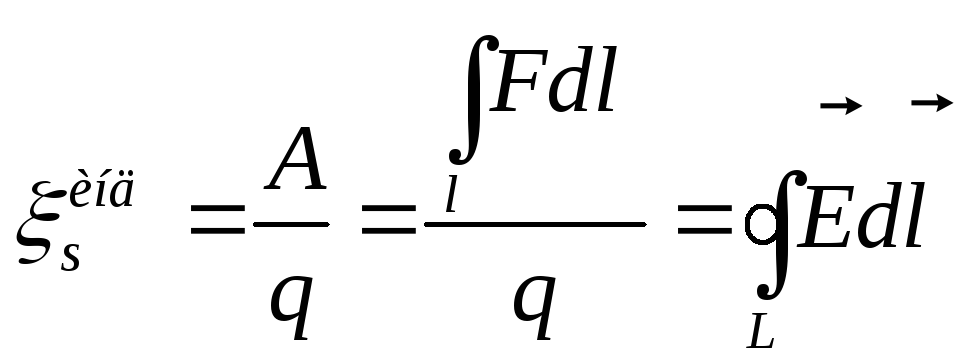(7.2)

ЭДС индукции равна циркуляции вектора напряжённости вдоль замкнутого контура.

- поток вектора индукции магнитного поля.

(7.3)

- нормаль к , - численное значение.

Подставим 7.3 и 7.2 в 7.1:

(7.4)

Это одно из уравнений Максвелла в интегральной форме и является обобщением закона электромагнитной индукции Фарадея.

Получим данное уравнение в дифференциальной форме, для этого применим теорему Стокса.

**

В правой части 7.4 стоит производная по времени, а интеграл берём по поверхности, то есть по координатам, поэтому производную и интеграл можно поменять местами.

может зависеть как от координат, так и от времени.

Интеграл равен 0, а так как он брался по произвольной поверхности, то и подынтегральное выражение тоже равно нулю.

(7.5)

Это уравнение Максвелла в дифференциальной форме, которое говорит о том, что изменяющееся во времени магнитное поле порождает вихревое электрическое поле. «-» - говорит о том, что вектор скорости изменения магнитной индукции и возникающая при этом в замкнутом контуре ЭДС индукции составляют левовинтовую систему.

Если в качестве контура выбрать силовую линию вектора напряженности

электрического поля, то элемент касательной и сонаправлены.

Возьмём от обеих частей уравнения 7.5 дивергенцию:

(7.6)

дивергенция зависит от координат, а производная берётся по времени, можем поменять их местами:

(7.7)

(7.8)

Опыты показали, что = 0

Это уравнение в дифференциальной форме, оно говорит о том, что не существует отдельных магнитных зарядов, на которых могли бы начинаться или обрываться силовые линии магнитного поля.