ГОС / 23

22. Закон сохранения энергии для системы зарядов и электромагнитного поля в вакууме. Плотность энергии и плотность потока энергии электромагнитного поля. Понятие об импульсе поля.

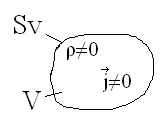
Рассмотрим в пространстве некоторый объем V, окруженный замкнутой поверхностью, в котором находятся заряды. Пусть эти заряды распределены с постоянной объемной плотностью ρ 0 и движутся ( 0).

Тогда эти заряды создают вокруг себя электромагнитное поле. Это поле производит работу по изменению состояния зарядов. Вычислим элементарную работу с точки зрения механики.

,

С другой стороны:

- мощность силы в единице объема

- мощность силы в элементе объема dV.

(7.1) – другое выражение для мощности.

N- мощность силы или работа, производимая электромагнитным полем по изменению состояния зарядов в единицу времени.

Вычислим эту мощность, воспользовавшись выражением для плотности силы

Рассмотрим второй интеграл отдельно:

, , ,

Физически это значит, что магнитное поле работу над зарядами не совершает, следовательно работу совершает только электрическое поле.

(7.2)

(7.3)

Воспользуемся III уравнением Максвелла и выразим .

III ;

.

Подставим в выражение для мощности:

={; } = =

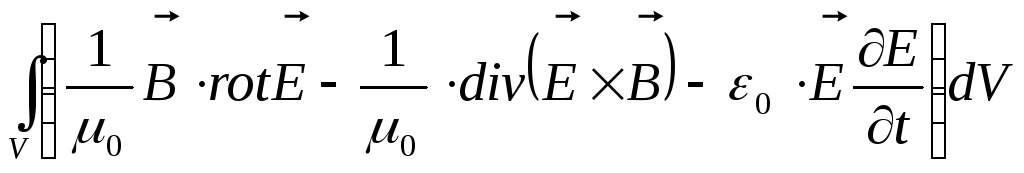= { II уравнение Максвелла } = =

= { ; }= =

= { }=

(7.4)

Производная зависит от времени, интеграл берется по координатам, следовательно, их можно поменять местами, тогда

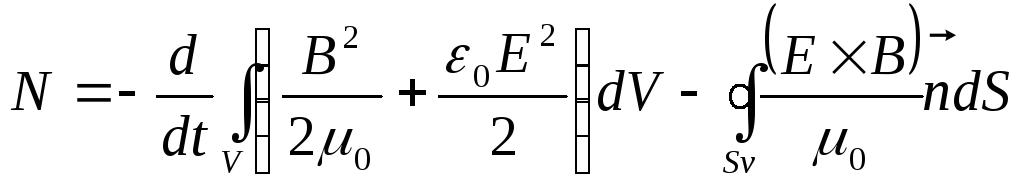(7.4’)

Устремим объем V к бесконечности, то есть рассмотрим все бесконечное пространство:

V; , 0.

Отсюда:

(7.5)

N- это работа электромагнитного поля по изменению состояния зарядов в единицу времени. А если меняется состояние зарядов, то меняется энергия электромагнитного поля, следовательно, можно сказать, что N- изменение энергии электромагнитного поля в единицу времени.

В выражении (7.5) 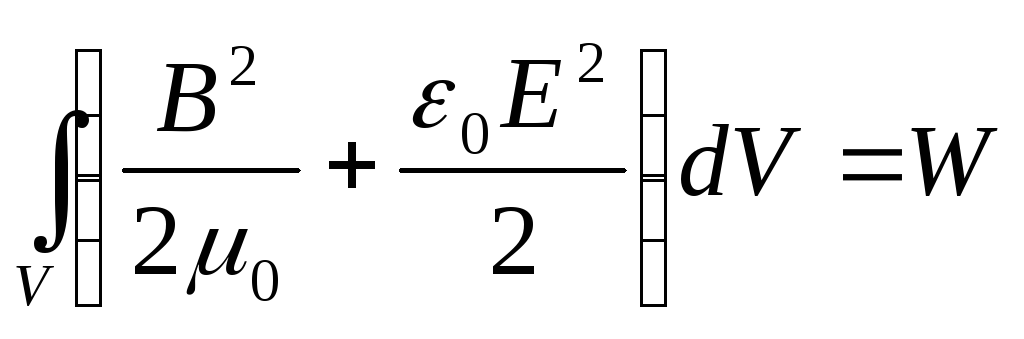(7.6)

(7.6) - энергия электромагнитного поля. Тогда выражение (7.5) говорит о том, что работа над зарядами совершается за счет убыли энергии электромагнитного поля.

Энергия электромагнитного поля в единице объема – плотность энергии w

(7.6’)

Рассмотрим конечный объем.

(7.7) – вектор Умова-Пойнтинга.

(7.8)

N - работа, совершаемая над зарядами в единицу времени.

- убыль энергии электромагнитного поля в объеме V за единицу времени.

- убыль энергии электромагнитного поля, а именно, количество энергии поля, вытекшее в единицу времени через замкнутую поверхность, ограничивающую объем, где есть заряды.

Скалярное произведение - количество энергии, вытекшее в единицу времени через единичную площадку с нормалью .

Сам вектор - вектор плотности потока энергии, указывающий направление распространения электромагнитного поля.

С учетом обозначений: (7.9) - данное выражение представляет собой закон сохранения энергии электромагнитного поля: убыль энергии электромагнитного поля идет на совершение работы над зарядами и на вытекание энергии через поверхность, ограничивающую объем, где есть заряды.

Пусть заряды распределены равномерно с объемной плотностью ρ и движутся со скоростью . Такие заряды создают вокруг себя электромагнитное поле. Электромагнитное поле действует на эти заряды с силой, которая согласно второму закону Ньютона () равна скорости изменения импульса заряженных частиц ()

(3.1)

С другой стороны

Воспользуемся выражением для плотности силы

(3.2)

Проделав выкладки предыдущего §2, можно получить закон сохранения импульса. Устремляя объем к бесконечности , (3.3)

В левой части стоит скорость изменения импульса заряженных частиц. Значит, правая часть имеет размерность скорости изменения импульса. Следовательно, интеграл, который стоит под знаком производной, имеет размерность импульса и называется импульсом электромагнитного поля и обозначается

(3.4) (3.5)

Скорость изменения импульса заряженных частиц равна скорости изменения импульса электромагнитного поля, взятого с противоположным знаком.

Перенесем правую часть влево, производные объединим

(3.6)

Получили закон сохранения импульса:

Полный импульс частиц электромагнитного поля сохраняется во времени. Импульс электромагнитного поля в единице объема называется плотностью импульса (3.7)

Плотность импульса электромагнитного поля отлична от нуля, если вектора и не равны нулю. А так же, если вектора и не параллельны. При этом говорят, что поле несет в себе движение.

Т.к. вектор Умова-Пойнтинга , то (3.8)

Если имеет место плотность потока энергии электромагнитного поля в пространстве, то электромагнитное поле обладает плотностью импульса, то есть несет в себе движение.

Плотность импульса и плотность энергии отличны от нуля в электромагнитном поле. В электростатическом поле эти вектора равны нулю (=0). В магнитостатическом поле не равно нулю, но энергия циркулирует вокруг зарядов и токов. И в переменном электромагнитном поле эти вектора не равны нулю, и при этом энергия и импульс могут отрываться от зарядов и токов.