Киселева Г.А. Математика часть 1

Рассмотрено на заседании кафедры математики, протокол № 2 от 07.10.08 г. Одобрено редакционно-издательской комиссией ФОМ и ЕНД ГОУ ВПО ЧГУ, прото-

кол № 2 от 21.10.08 г.

Составитель : Г.А. Киселева

Рецензенты : Г.В. Карпова, доцент (ГОУ ВПО ЧГУ); А.В. Толстиков, канд. физ.-мат. наук, проф. (ГОУ ВПО ЧГУ)

Научный редактор : Н.Н. Беляева, канд. пед. наук, проф.

© Киселева Г.А., 2009

© ГОУ ВПО «Череповецкий государственный университет», 2009

2

Введение

Данное учебно-методическое пособие предназначено для студентов экономических специальностей как дневной, так и заочной форм обучения.

Пособие содержит контрольные работы по темам «Аналитическая геометрия на плоскости и в пространстве», «Введение в анализ».

Задания в контрольных работах составлены с учетом требований Государственного стандарта по специальностям: 080507 «Менеджмент организации», 080500 «Менеджмент», 080504 «Государственное и муниципальное управление», 080505 «Управление персоналом».

Пособие поможет студентам самостоятельно подготовиться к контрольным работам, восполнить обнаруженные в знаниях пробелы и выполнить предложенные контрольные работы качественно.

Контрольная работа 1.1

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ

Краткие теоретические сведения

1. Прямая на плоскости

1.1. Различные способы задания прямой на плоскости

Уравнение прямой (рис. 1), проходящей через заданную точку M 0 (x 0; y 0) перпендикулярно заданному вектору n A; B , име-

n

М0

Рис. 1

Вектор n называется вектором нормали прямой.

Общее уравнение прямой имеет вид

A x + B y + C = 0.

Уравнение прямой (рис. 2), проходящей через заданную точку M 0 (x 0; y 0) параллельно заданному вектору s m; n , имеет вид

s

М0

Рис. 2

Вектор s называется направляющим вектором прямой.

Уравнение прямой с угловым коэффициентом (рис. 3) имеет вид

y = k x + b,

где k = tg .

4

y

0 x

b

Рис. 3

Уравнение прямой, проходящей через две заданные точки M 1 (x 1; y 1) и M 2 (x 2; y 2) (рис. 4), имеет вид

M 2

M 1

Рис. 4

Уравнение прямой в отрезках (рис. 5) имеет вид

ax by 1.

y

b

0 a x

Рис. 5

5

1.2. Основные задачи на прямую на плоскости

Расстояние d от точки M 0 (x 0; y 0) до прямой (l): A x + B y + + C = 0 (рис. 6) равно

2. Кривые второго порядка

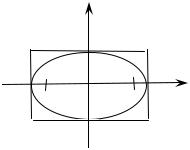
2.1. Эллипс

Каноническое уравнение эллипса с центром в точке (0; 0) и полуосями а и b (рис. 7, 8) имеет вид

(0 < ε < 1), F 1, F 2 – фокусы эллипса

Рис. 7

7

y

–b

Рис. 8

Каноническое уравнение эллипса с центром в точке (x0; y0) и полуосями а и b (рис. 9) имеет вид

y

b

a

y0

х0 x

Рис. 9

2.2. Окружность

Каноническое уравнение окружности с центром в точке (x0; y0) и радиусом R (рис. 10) имеет вид

8

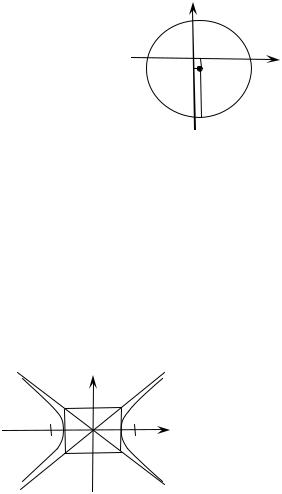
(x – x 0) 2 + (y – y 0) 2 = R 2.

у

0 x0

R

Рис. 10

2.1. Гипербола

Каноническое уравнение гиперболы с центром в точке (0; 0), с действительной полуосью a и мнимой полуосью b (рис. 11) имеет вид

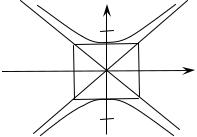
Каноническое уравнение гиперболы с центром в точке (0; 0), с действительной полуосью b и мнимой полуосью a (рис. 12) имеет вид

9

Канонические уравнения гиперболы с центром в точке (x 0; y 0) имеют вид

2.4. Парабола

Канонические уравнения параболы с вершиной в точке (0; 0) (рис. 13-16) имеют вид

10