
Киселева Г.А. Математика часть 1
.pdf
Логарифмические функции (рис. 30, 31).
y = log a x, y |
|
y = log a x, y |
|
|
|
|
|
|
|
a > 1 |
|
0 < a < 1 |
|
|
0 1 |
x |
0 |
1 |
x |
Рис. 30 Рис. 31
Тригонометрические функции (рис. 32 - 35).
y = sin x |
y |
|
1 |
|
3π |
– |
|
π |
0 |
π |
|
|
3π |
|
x |
2 |
|
2 |
|
|
|||||||
|
2 |
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
–1 |
|
|
|
|
|
|
|
|
|
|
Рис. 32 |
|
|
|
|
|
|
|
y = cos x |
|
|
y |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
3π |
– |
|
π 0 |
π |
|
|
|
3π |
2 |
x |
|
|
2 |
|
2 |
2 |
|
|
|
2 |
|
||
|
|
|
|
– 1 |
|
|
|
|
|
|
|
Рис. 33
31

y = tg x
y
3π |
– |
|
π |
0 |
π |
|
3π |
x |
2 |
|
2 |
|
|
||||
2 |
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
Рис. 34
y = сtg x
y
– |
|
π |
0 |
π |
|
3π |
2 |
x |
|
2 |
|
2 |
|
2 |
|
Рис. 35
32
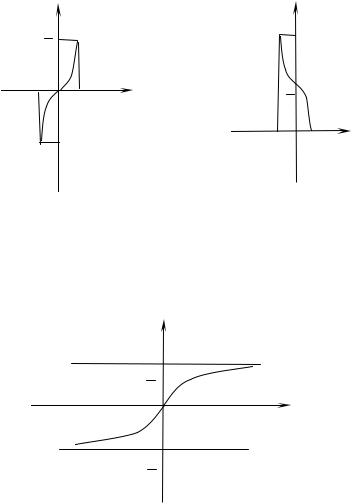
Обратные тригонометрические функции (рис. 36 - 39).
y = arcsin x
y
π
2
–1 |
0 1 |
x |
|
|
π |
|
|
2 |
|
|
|
|
|
|
|
Рис. 36
y = arсtg x |
y |
|
π
2
0
π2
y = arccos x
y
π
2
–1 0 1 x
Рис. 37
x
Рис. 38
33

y = arcсtg x |
y |
|
π
2
0 |
x |
Рис. 39
Замечание. При нахождении пределов следует помнить, что:
[a + ] = + , [a – ] = 0, |
|
если a > 1. |
|
||||||||
[a + ] = 0, [a – ] = + , |
если 0 < a < 1. |
|
|||||||||
[e + ] = + , [e – ] = 0. |
|
|
|
|
|
|
|||||
[log a ( + )] = + , |
[log a (0 +)] = – , |
если a > 1. |
|||||||||
[log a ( + )] = – , |
[log a (0 +)] = + , |
если 0 < a < 1. |
|||||||||
[ln ( + )] = + , [ln (0 +)] = – . |
|
||||||||||
|
|
π |
|
|
|
|
|
π |
|
|
|
tg |
|
, |
tg |
|
|
|
. |
|
|||
2 |
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
arctg π2 .
34
3.2. Точки разрыва функции, их классификация
Функция f (x) называется непрерывной в точке x0, если:
– функция определена в точке x0;
– существует конечный |
lim f x ; |
||
|
|
x x0 |
|
– lim f x f x0 . |
|
|
|
x x0 |
|
|
|
Или: lim |
f x lim f |
x f x |
. |
x x |
x x |
0 |
|
0 |
0 |
|
|
Точка, в которой функция не является непрерывной, называ-
ется точкой разрыва функции.
Классификация точек разрыва.
1) Если в точке разрыва существуют конечные односторонние пределы, то это точка разрыва I рода. При этом если
lim |
f x lim |
f x f x |
, |
x x |
x x |
0 |
|
0 |
0 |
|
|
то разрыв называют устранимым.
2) Если в точке разрыва хотя бы один из односторонних пределов не существует или равен бесконечности, то это точка разрыва II рода.
35

Решение примерного варианта контрольной работы
Задача 1. Решить неравенство.
|
|
|
|
|
|
|
|
3x 4 |
|
1. |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x 4 |
|
1 |
1 |
|
3x 4 |
|
1 –2 3x + 4 2 |
||||||
|
|
|
||||||||||||
|
|
|
2 |
|
|
|||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
–6 3x –2 2 x |
2 |
. |
||||||||
|
|
|
|
3 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
x 2; |
|
. |
|
|
|
|
|
|
|
|||||
3 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 2. Найти область определения функции.
y |
x 4 |
x |
ln 39 x . |
|
x 5 |
||||
|
|
|
Решение
x 4 |
0, |
|
x 4, |
|
0, |
|
|
x 5 |
x 5, |
||
|
|
|
|
39 x 0 |
|
x 39. |
|
Ответ: |
x [4; 5) |
(5; 39). |
|
36

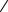
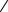
 4
4 
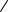 5
5
 39
39

Задача 3. |
|
Вычислить пределы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1) |
|
lim |
n |
|
n 1 |
n . |
|
3) |
lim |
|
cos x cos3 x |
. |
|||||||||||||||
|
|
|
|
|
|
|
tg |
2 |
2x |
||||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|||||
|
|
|
x2 x 12 |
. |
|
|
|
4) |
|
|
x 5 |
3x |
|
|
|||||||||||||
2) |
|
lim |
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
. |
|
|
|||||
2x |
2 |
9x |
|
9 |
|
|
|
|
x |
|
|
||||||||||||||||
|
|
x 3 |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||||||||||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1) |
|
lim |
n |
n 1 |
n = [ ( – )] = |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
n |
n 1 |
|
n |
n 1 |
n |
= |
|
lim |
|
n n 1 n |
= |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
n |
|
|
|
|
n 1 |
n |
|
|
|
n |
|
|
n 1 |
|
n |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
n |
|
|
|
|
|
|
Поскольку n + 1 n при n , то |
|||||||||||||||||
= lim |
|
|
|
|
|
|
|
|
. |
||||||||||||||||||
|
n 1 |
|
|
|
|||||||||||||||||||||||
n |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
придем к пределу |
lim |
|
n |
= lim |
|
n |
|
1 |
. |
|
|
|
|
|
|||||||||||||
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
n |
n n |
n 2 n |
|
|
|
|
|
|
|
|
|
||||||||
Ответ: 12 .
|
x2 x 12 |
= |
0 |
|
|||
2) lim |
|
|
|
|
|
. |
|
2x |
2 |
9x 9 |
0 |
||||
x 3 |
|
|
|
|
|||
Разложим числитель и знаменатель на множители:
x 2 + x – 12 = 0, |
2 x 2 – 9 x + 9 = 0, |
D = 1 + 48 = 49, |
D = 81 – 72 = 9, |
37

|
|
x 1 49 |
|
4 , |
|
|
|
|
|
|
x |
9 9 |
|
|
3 |
, |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
4 |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
x |
1 49 |
|
3, |
|
|
|
|
|
|
|
x |
9 9 |
3, |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||
|
x |
|
|
+ x – 12 = |
|
|
|
|
|
|
|
|
|
|
|
2x |
|
– 9x + 9 = 2 |
x |
|
x 3 = |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
= (x + 4) (x – 3). |
|
|
|
|
|
|
|
|
|
|
|
= (2x – 3) (x – 3). |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
Придем к пределу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
lim |
|
x2 x 12 |
|
= lim |
x 4 x 3 |
|
= lim |
x 4 |
|
|
|
= |
3 4 |
|
7 |
. |
|
||||||||||||||||||||||||||||||
|
|
2x2 9x 9 |
|
2x 3 x 3 |
|
2x 3 |
2 3 3 |
3 |
|
|||||||||||||||||||||||||||||||||||||||
|
x 3 |
|
|
x 3 |
|
|
|
|
|
x 3 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
Ответ: |
|
7 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
cos x cos3 x |
|
|
0 |
|
|
cos x |
1 cos2 x |
|
|
|
|
|
cos xsin2 x |
|
|||||||||||||||||||||||||||
|
3) |
|
lim |
|
|
|
|
|
|
|
|
|
|
= |
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
= |
||||||||||
|
|
|
|
tg |
2 |
2x |
|
|
|
|
|
tg |
2 |
2x |
|
|
|
|
|
|
tg |
2 |
2x |
|||||||||||||||||||||||||
|
|
|
|
|
x 0 |
|
|
|
|
|
0 |
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= |
|
|
|
. Поскольку sin x x, |
tg 2x 2x |
при x 0, то придем к |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
пределу |
lim |
cos x x2 |
|
= lim |
|
cos x |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
2x 2 |
|
4 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
x 0 |
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Ответ: 14 .
38
|
|
lim |
x 5 |
3x |
|
|
|
|
|
|
lim |
x |
|
5 |
|
3x |
= lim |
1 |
5 |
3x |
||||||||||||
4) |
|
|
|
|
= |
= |
|
= |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
x |
x |
|
|
|
|
|
|
|
x |
|
x |
|
|
x |
|
x |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
5 |
3x |
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
5 |
|
|
x |
|
5 |
|
|
x |
|
|
|
|
|
|
|
||||||||||
1 |
= lim |
1 |
|
|
|
5 |
|
|
= lim 1 |
|
5 |
|
. |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
x |
|
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Используя второй замечательный предел, получим
lim e15 e15 . x
О т в е т : e 15.
Задача 4. Исследовать функцию на непрерывность и построить ее график (схематично).
|
|
|
|
|
|
|
|
|
|
|
|
ln ( x), |
|
|
x 0, |
|
|||||||
|
|
|
π |
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|||||
y tg x |
|
|
, |
0 x |
|
|
, |
||||
2 |
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
π |
|
|
|
|
sin x, |
|
|
|
x |
|
. |
|
||||
|
|
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|||
Решение |
|
|
|
|
|
|
|
|
|
|
|
1) Построим графики. |
|
|
|
|
|
|
|
|
|
|
|
График функции y = ln (– x) |
при x < 0. |
|
|
||||||||
Данный график получается из графика |
y = ln x зеркальным |
||||||||||
отражением относительно оси OY. Рассмотрим график на промежутке (– ; 0).
39

|
y |
y = ln (–x) |
y = ln x |
|
1 |
–1 |
1 x |
|
–1 |
|
|
График функции y tg x |
π |
при 0 x |
π |
. |
|||||
|
|
|
|
|
|
2 |
|
2 |
|
||
|
|
Данный график получается из графика |
y = tg x сдвигом на |
||||||||
π |
вдоль оси OX вправо. |
Рассмотрим график на промежутке |
|||||||||
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
π |
|
|
|
|
|
|
|
|
0; |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
|
|
|
|
|
y = tg x |
|
π |
|
|
y tg x |
|
|
|
2 |
||
y |
|
|
|
|
|
|
|
– |
|
π |
–1 |
0 1 |
π |
|
3π |
x |
|
|
2 |
|
|
2 |
|
2 |
|
40
