Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Череповецкий Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Киселева Г.А. Математика часть 1

.pdf

Скачиваний:

Добавлен:

22.03.2015

Размер:

327.61 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

–4 x + 4 (у + 6) – 4 (z – 2) = 0,

или x – (у + 6) + (z – 2) = 0,

или

x – у + z – 8 = 0 – уравнение

(АBC).

Пусть DD / – высота, опущенная из точки

на плоскость

АBC. Тогда (DD /) (АBC),

sDD

nABC .

Из уравнения плоскости АBC найдем nABC 1; 1; 1 .

Уравнение

DD /

найдем по формуле

(7); D (1; 0; –2),

s DD 1; 1; 1 :

x 1

y 0

z 2

или

x 1

z 2

2) Проекцией точки D на плоскость АBC будет точка D /. Для нахождения ее координат воспользуемся формулой (8):

x y z 8 0,

x 1 t 1,y 1 t 0,

z 1 t 2,

x t 1,		t 3,

y t,		x 4,

z t 2,	8 0	y 3,
t 1 t t 2	8 0	z 1.

Таким образом, D / (4; –3; 1).
Ответ: 1)	x 1	y		z 2	;
	1	1
			1
2) D / (4; –3;			1).

Контрольная работа 1.2

ВВЕДЕНИЕ В АНАЛИЗ

Краткие теоретические сведения

1. Абсолютная величина числа

1.1. Определение

Абсолютной величиной, или модулем действительного числа x называется само число x, если x неотрицательно, и противоположное число (–x), если x отрицательно:

x, если x 0,

xx, если x 0.

Абсолютная величина разности двух чисел | x – a | означает расстояние между точками x и a числовой прямой.

1.2. Свойства

| x | 0.

3) | x y | = | x | | y |.

5) | x + y | | x | + | y |.

| –x | = | x |.

6) | x – y | | x | – | y |.

1.3. Решение неравенств с модулем

| x – a | < b,

где

b > 0.

– b < x – a < b,

a – b < x < a + b.

| x – a | > b,

где

b > 0.

x a b,x a b.

2. Предел функции

2.1. Основные свойства пределов

lim f x g x = lim f x lim g x .

x a

lim f x g x = lim f x lim g x .

x a

lim f x

lim g x 0.

lim

x a

при

lim g x

x a

lim c

f x

= c lim f

(c = const).

x a

lim

lim f

2.2. Бесконечно малые и бесконечно большие функции

Определение.

Функция

f (x) называется бесконечно малой

в точке a, если lim f x 0.

x a

Функция

f (x) называется бесконечно большой в точке a, ес-

ли lim f x .

x a

2) Свойства

Если f (x), g (x) бесконечно малые (бесконечно большие) функции в точке a, то f (x) + g (x) также будет бесконечно малой (бесконечно большой) функцией в точке a.

Произведение бесконечно малой (бесконечно большой) функции на бесконечно малую (бесконечно большую), ограниченную, постоянную функции есть бесконечно малая (бесконечно большая) функция.

Если f (x) бесконечно малая функция в точке a, то

–

f x

бесконечно большая функция в точке a и наоборот.

3) Сравнение

Бесконечно малые (бесконечно большие) в точке

функции

f (x)

и g (x)

называются эквивалентными, если

lim

f x

1 .

x a

g x

Обозначение:

f (x) g (x)

при x a.

Теорема.

Если

f (x) f 1

(x), g (x) g 1 (x)

при

x a

существует

lim

, то существует lim

. При этом

f x

x a

lim

f1 x

g x

x a

Замечание. Все вышесказанное (п. 2.1, 2.2) имеет место и при x , x a .

2.3. Замечательные пределы

1) Первый замечательный предел:

lim sin x 1 .

x 0 x

2) Следствия из первого замечательного предела:

при x 0

sin x x, sin x x, tg x x.

3) Второй замечательный предел:

	1	x	e .
lim 1
lim 1	x
x	x

4) Следствия из второго замечательного предела:

			1
	lim		1 x			e,
				x
	x 0
lim	loga 1 x				loga e,
			x
x 0
	lim	ln 1 x				1.

	x 0		x

2.4. Основные приемы раскрытия неопределенностей

При нахождении пределов могут встретиться неопределенности вида

	0	,	,	[0 ],	[ – ],	[1 ].

0

1)Раскрытие неопределенности вида 0 .

Если под знаком предела алгебраическая дробь, то ее следует преобразовать таким образом, чтобы в числителе и знаменателе выделить множитель (x – a), затем сократить на него.

П р и м е р

3 x 18

lim

x 3 x 6

lim

x 3 x

3x 9

x 3

= lim

x 6

x 3

x2 3x 9

27 3

Если под знаком предела дробь, содержащая иррациональность, то следует избавиться от иррациональности, домножая на сопряженный множитель.

П р и м е р

	x 2 6	0			x 2 6	x 2 6		=
lim				lim
	x 8		0		x 8 x 2		6
x 8				x 8

= lim

x 2

2 6 2

lim

х 2 6

x 8

x 2 6

x 8

x 2 6

x 8

= lim

x 8

x 2 6

6 6

2 6

Если под знаком предела дробь, содержащая тригонометрические функции, то используем первый замечательный предел или следствия из него.

П р и м е р

lim		3x sin 5 x				0	lim

	1		cos	2	x
x 0						0		x 0
sin x x,			sin 5 x 5 x, то					lim
								x 0

	3x sin 5 x		. Поскольку при x 0

	sin 2 x
3xsin 5 x		lim		3x5 x	15 .
	sin2 x			x2
			x 0

2)Раскрытие неопределенности вида .

Неопределенность вида возникает в тех случаях, когда

под знаком предела стоит рациональная дробь или дробь, содержащая иррациональность. В этом случае используют эквивалентные бесконечно большие функции:

a 0 x n + a 1 x n – 1 + + a n – 1 x + a n a 0 x n

при x .

П р и м е р

lim

1 15x 4 x

x 1 – 15x +

. Поскольку при

x 3

6 x

+ 4x 3 4x 3, 6x 2 + x 9

– 7 x 9, то данный предел равен lim

4x3

x 3 x9

=4.

3)Раскрытие неопределенностей вида [0 ] и [ – ].

Неопределенности [0 ] и [ – ] путем тождественных преобразований функции, стоящей под знаком предела, сводятся

к неопределенности вида	0		или
				.
		0

П р и м е р ы

1) lim x sin 2 x ctg 2 3 x = [0 ]. Поскольку

ctg 3 x

tg 3 x

x 0

то исходный предел равен lim

x sin 2 x

. Поскольку

3 x

x 0

sin 2x 2x,

3x 3x

при x 0,

то придем к пределу

lim

x 2 x

2 .

3x 2

x 0

lim

x2 8x x2

= [ – ] =

= lim

x2 8x x2 8x x2 8x

x2 8x

= lim

8x x2 8x

= lim

x2 8x x2

x2 8x

16x

= lim

Поскольку

при

x x2 8x x2 8x

+ 8x x 2,

x 2 – 8x x 2, то придем к пределу

lim

16x

= lim

16x

= 8.

2 x

4) Раскрытие неопределенности вида [1 ].

В таких случаях используют второй замечательный предел или следствия из него.

П р и м е р

x 3	x
lim		.

x x 2

Будем выделять второй замечательный предел путем тождественных преобразований:

x 3	x		5 x		=
lim		lim 1	x 2	1	=
x x 2		x	x 2

			5		x
	5	x 2		x 2	x
	5	5
lim 1						.
lim 1	x 2					.
	x 2
x

Используя второй замечательный предел, получим lim e					5x
Используя второй замечательный предел, получим lim e					x 2
				x
lim	5 x
lim	x 2	. Поскольку x – 2	x при	x , то придем к пределу
= e x		. Поскольку x – 2	x при	x , то придем к пределу
lim 5 x	e5 .
e x x	e5 .

Замечание. При нахождении пределов следует помнить, что:

1			1		0			; [0 + 0] = 0; [ + ] = .
	0	;		;		0 ;	0
			0

3. Непрерывность функции

3.1. Графики основных элементарных функций

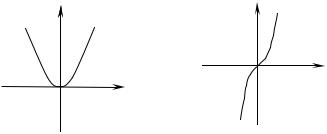
Степенные функции (рис. 22 - 27).

					y = x 2n + 1,
y = x	2n	,	y	y	y = x 2n + 1,
y = x		,	y	y	n N
n N					n N
n N
				0	x
				0
			0	x
			0	x
			Рис. 22		Рис. 23

y	1	,	y		y		1	y
	1		y				1	,
	x2 n
						x	2 n 1
						x	2 n 1
n N					n N
			0	x				0
			0	x				0
								x

Рис. 24			Рис. 25
y		y 3 x	y
y x
0	x		0	x

Рис. 26

Рис. 27

Показательные функции (рис. 28, 29).

			y = a x,
x
x
y = a ,	y		0 < a < 1	y
a > 1	1		0 < a < 1	y




					1
					1
	0	x

				0		x
				0		x

Рис. 28			Рис. 29
Рис. 28			Рис. 29

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.07.201922.93 Кб6Кейс 2.docx
#
28.08.2019241.66 Кб4Кейс по Северстали.doc
#
18.07.2019103.42 Кб17КЕЙСЫ.doc
#
22.03.201535.92 Кб20Киевская Русь в 11.docx
#
24.12.2018258.05 Кб8КИМ геология.doc
#
22.03.2015327.61 Кб15Киселева Г.А. Математика часть 1.pdf
#
22.03.2015395.18 Кб16Киселева Г.А. Математика часть 2.pdf
#
22.03.2015416.05 Кб18Киселева Г.А. Математика часть 3.pdf
#
20.04.2019145.92 Кб21Классификация нарушений речи.doc
#
22.03.2015603.44 Кб15книга об англо-бурской войне.rtf
#
16.08.20195.84 Mб57Козлов Г.С. Термическая обработка стали курс ле...doc