
Киселева Г.А. Математика часть 1
.pdf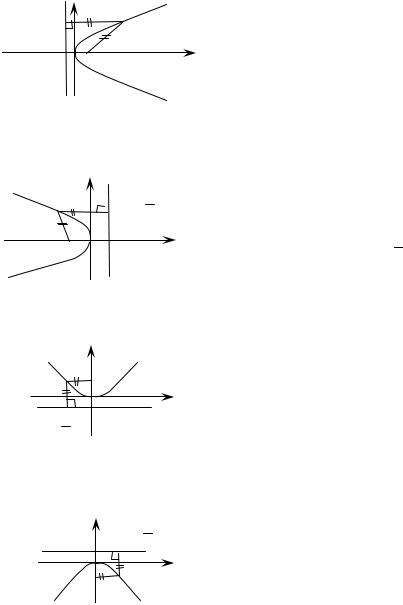
|
|
у |
|
y2 = 2 pх, |
F |
p |
; 0 , |
|
|
|
p |
|
|
||||||
|
|
|
|||||||
|
|
|
|
|
2 |
|
|
||
x 2 |
х |
|
|
||||||
|
|
|
|
|
|
||||
|
|
0 F |
F – фокус параболы, p – параметр |
||||||
|
|
|
|
параболы (p > 0), прямая x |
p |
– |
|||
|
|
|
|
|
|||||
|
|
|
|
директриса |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 13 |
|
|
|
|
|
|
|
|
у |
p |
|
x |
|
|
|
2 |
|
0 |
|
F |
х |
|
y |
2 |
|
|
|
p |
|
|
|
|
= – 2 px, |
F |
|
|
; 0 |
|
, |
|
|
2 |
|||||||
|
|
|
|
|
|
|
|
F – фокус параболы, p – параметр параболы (p > 0), прямая x 2p –
директриса
Рис. 14
у |
F |
|
y p |
0 |
х |
|
||
2 |
|
|
Рис. 15 |
|
|
у |
y |
p |
|
2 |
|
0 |
|
х |
F |
|
|
|
|
|
Рис. 16 |
|
|
x |
2 |
|
|
|
p |
|
|
|
= 2 p y, |
F |
0; |
|
|
, |
|
|
2 |
||||||
|
|
|
|
|
|
|
|
F – фокус параболы, p – параметр
параболы (p > 0), прямая у |
p |
– |
|
||
2 |
|
|
директриса |
|
|
|
2 |
|
|
|
p |
|
|
x |
|
= – 2 p y , F |
0; |
|
|
|
, |
|
2 |
||||||
|
|
|
|
|
|
|
|
F – фокус параболы, p – параметр
параболы (p > 0), прямая у |
p |
– |
|
2 |
|||
директриса |
|
||
|
|
11
Канонические уравнения параболы с вершиной в точке (x 0; y 0) имеют вид
(y – y0) 2 = 2 p (x – x0), (x – x0) 2 = 2 p (y – y0).
3. Плоскость
3.1. Различные виды уравнений плоскости
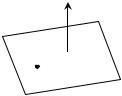
Уравнение плоскости (рис. 17), проходящей через заданную точку M 0 (x 0; y 0; z 0) перпендикулярно заданному вектору
n A; B;C , имеет вид
A (x – x0) + B (y – y 0) + C (z – z 0) = 0.
n
M 0
Рис. 17
Вектор n называется вектором нормали плоскости.
Общее уравнение плоскости имеет вид
A x + B y + C z + D = 0.
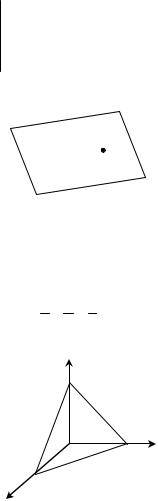
Уравнение плоскости (рис. 18), проходящей через три задан-
ные точки M 1(x 1; y 1; z 1), M 2 (x 2; y 2; z 2) и M 3 (x 3; y 3; z 3), име-
ет вид
12
x x1 |
y y1 |
z z1 |
|
|
x2 x1 |
y 2 y1 |
z 2 z1 |
0 . |
(6) |
x3 x1 |
y3 y1 |
z3 z1 |
|
|
M 2 
M 1 M 3
M 3
Рис. 18
Уравнение плоскости в отрезках (рис. 19) имеет вид
ax by cz 1.
z c
|
b |
0 |
y |
a
x
Рис. 19
3.2. Основные задачи на плоскость
Расстояние d от точки М0 (x 0; y 0; z 0) до плоскости A x + B y + + C z + D = 0 равно
13

|
d |
A x0 |
B y0 C z 0 D |
|
. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
A2 B2 C2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||
Взаимное расположение плоскостей: |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||
уравнение плоскости 1 |
|
A 1 x + B 1 y + C 1 z + D 1 = 0 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||
уравнение плоскости 2 |
|
A 2 x + B 2 y + C 2 z + D 2 = 0 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
угол φ между плоскостя- |
|
arccos |
|
A1 A2 B1 B2 C1 C 2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||
ми 1 и 2 |
|
|
|
|
A12 B12 C12 |
A22 B22 C22 |
|||||||
|
|
|
|
|
|
|
|
||||||
условие |
параллельности |
|
|
|
A1 |
B1 |
C1 |
||||||
1 2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
A2 |
B2 |
C 2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
условие |
перпендикуляр- |
|
А1 А2 + B 1 B 2 + C 1 C 2 = 0 |
||||||||||
ности 1 |
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
4. Прямая в пространстве
4.1. Различные виды уравнений прямой в пространстве
Уравнение прямой (рис. 20), проходящей через заданную точку M 0 (x 0; y 0; z 0) параллельно заданному вектору s m; n; p , имеет вид
x x0 |
|
y y0 |
|
z z0 |
– канонические уравнения. (7) |
|
m |
n |
p |
||||
|
|
|
s
 M 0
M 0
Рис. 20
14

Вектор s называется направляющим вектором прямой.
Параметрические уравнения прямой в пространстве имеют вид
x mt x0 ,
y nt y0 ,z pt z 0 .
Общие уравнения прямой в пространстве (как линия пересечения двух плоскостей) имеют вид
A x B |
y C |
z D 0, |
||
|
1 |
1 |
1 |
1 |
|
|
|
|
|
A2 x B2 y C2 z D2 0.
Уравнение прямой (рис. 21), проходящей через две заданные точки M 1 (x 1; y 1; z 1) и M 2 (x 2; y 2; z 2), имеет вид
x x1 |
|
y y1 |
|
z z1 |
. |
|
x2 x1 |
y2 y1 |
z 2 z1 |
||||
|
|
|
M 2
M 1
Рис. 21
15

4.2. Взаимное расположение двух прямых в пространстве:
уравнение прямой l 1 |
|
|
x x1 |
|
|
y y1 |
|
|
z z1 |
|
|||||||||||
|
|
|
m1 |
|
n1 |
|
p1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
уравнение прямой l 2 |
|
x x 2 |
|
|
y y 2 |
|
|
z z 2 |
|
||||||||||||
|
|
m2 |
|
n2 |
|
p2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
угол φ между прямыми l 1 |
arccos |
|
|
m1 m2 n1 n2 p1 p 2 |
|
||||||||||||||||
и l 2 |
|
m12 |
n12 p12 |
|
m22 n22 p22 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
условие |
параллельности |
|
|
|
|
m1 |
|
n1 |
|
p1 |
|||||||||||
l 1 l 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
m2 |
n2 |
|
p 2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
условие |
перпендикуляр- |
m 1 m 2 + n 1 n 2 + p 1 p 2 = 0 |
|||||||||||||||||||
ности l 1 l 2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4.3. Взаимное расположение прямой и плоскости в пространстве:
уравнение плоскости |
|
A x + B y + C z + D = 0 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уравнение прямой l |
|
|
x x0 |
|
|
y y 0 |
|
z z |
0 |
|
|
|||
|
|
m |
|
|
n |
p |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
угол φ между прямой l и плоско- |
arcsin |
|
|
Am B n Cp |
|
|
|
|||||||
|
A2 B 2 C 2 |
m2 n2 p2 |
||||||||||||
стью |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
условие параллельности прямой и |
|
|
Am B n Cp 0 |
|
|
|
||||||||
плоскости l |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
условие перпендикулярности пря- |
|
|
|
A |
|
|
B |
C |
|
|
|
|
||
мой и плоскости l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
n |
p |
|
|
|
|
||||
|
|
|
|
|
|
|
||||||||
|
|
|
Ax By Cz D 0, |
|
|
|
||||||||
точка пересечения прямой и |
|
|
|
|
x0 , |
|
|
|
|
|
|
|||
|
|
x mt |
|
|
|
(8) |
||||||||
плоскости l |
|
|
y nt y , |
|
|
|
||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z pt z0 |
|
|
|
|
|
|
|||||
16
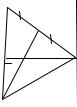
Решение примерного варианта контрольной работы
Задача 1. Даны координаты вершин треугольника A (–6; –2),
|
|
|
|
B (–3; |
2), C (–8; 4). Найдите: |
B |
|
|
N |
1) |
уравнение стороны АB; |
|
|
2) |
уравнение медианы АE; |
||
|
|
E |
|||
|
|
3) |
уравнение и длину высоты CD; |
||
|
|
|
|
||
D |
|
|
С |
4) |
уравнение прямой CN, параллель- |
|
|
||||
|
|
ной AB. |
|||
|
|
||||
|
|
|
|||
AРешение
1)Найдем уравнение стороны АВ по
|
|
формуле (3); A (–6; –2), B (–3; 2): |
|||||
x ( 6) |
= |
y ( 2) |
|
x 6 |
|
y 2 |
4 x – 3 y + 18 = 0. |
3 ( 6) |
2 ( 2) |
3 |
|
||||
|
|
4 |
|
||||
2) Точка E – середина отрезка BC. Найдем координаты точки E по координатам B (–3; 2) и C (–8; 4):
|
|
|
|
|
|
|
xE |
xB xC |
= |
3 ( 8) = |
11 |
; |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
y |
B |
y |
|
|
2 4 |
|
|
|
|
|
|
|
11 |
|
|
|||||||
|
|
|
|
yE |
|
|
|
|
|
C |
|
= |
|
|
|
|
|
= 3 |
E |
|
|
|
|
; 3 |
. |
|||||
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Найдем уравнение медианы |
|
|
AE |
|
по формуле (3); A (–6; –2), |
|||||||||||||||||||||||||
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
; 3 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 6 |
|
y 2 |
|
|
|
x 6 |
|
|
y 2 |
|
10 x – y + 58 = 0. |
|||||||||||||||||
|
|
11 |
6 |
3 2 |
|
|
|
|
1 |
|
|
5 |
|
|||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |

3) Так как CD – высота, то CD АB |
|
|
|
|
|
|
. Найдем |
|||||||||||||||||||||||||||||||
nCD AB |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
по координатам A (–6; –2) |
и B (–3; |
2): |
|
||||||||||||||||||||||||||||
координаты AB |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 6 ; 2 2 3; 4 . |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
AB |
|
|
|
|
|
|||||||||||||||||||||||||||||||
Найдем уравнение |
высоты CD по формуле (1); |
C (–8; |
4), |
|||||||||||||||||||||||||||||||||||
nCD (3; 4): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3 (x – (-8)) + 4 (y – 4) = 0 3 x + 4 y + 8= 0. |
|
|
|
|||||||||||||||||||||||||||||||||||
Длину высоты CD найдем |
по |
|
формуле (4); |
C (–8; |
4), |
|||||||||||||||||||||||||||||||||
(АB) : 4x – 3y + 18 = 0: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
d |
|
|
4 8 3 4 18 |
|
|
|
|
|
26 |
|
|
|
|
26 |
5, 2; |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
42 3 2 |
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|CD| = 5,2 |
(ед.). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
4) Так как прямая |
CN // АB, |
то |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
S |
CN |
|
AB |
. |
Найдем урав- |
||||||||||||||||||||||||||||||||
нение прямой CN по формуле (2); |
C (–8; |
4), |
|
|
|
CN |
3; 4 : |
|
||||||||||||||||||||||||||||||
|
S |
|
||||||||||||||||||||||||||||||||||||
|
x 8 |
|
|
y 4 |
4x – 3 y + 44 = 0. |
|
|
|
|
|
||||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Ответ: 1) (АB): 4 x – 3 y + 18 = 0.
2)(AE): 10 x – y + 58 = 0.
3)(CD): 3 x + 4 y + 8 = 0; |CD| = 5,2 (ед.).
4)(CN): 4x – 3 y + 44 = 0.
18

Задача 2. Дано уравнение кривой второго порядка
x 2 – 4y 2 + 8 x – 24y – 24 = 0.
Определите тип кривой, приведите уравнение к каноническому виду, укажите основные характеристики кривой, постройте кривую.
Решение
Так как коэффициенты при x 2 и y 2 отличны от нуля и имеют разные знаки, то, следовательно, данное уравнение на плоскости задает гиперболу. Для приведения уравнения к каноническому виду выделим полные квадраты:
x 2 – 4 y 2 + 8 x – 24 y – 24 = 0, (x 2 + 8 x) – 4 (y 2 + 6 y) – 24 = 0,
(x 2 + 2 x 4 + 4 2) – 4 2 – 4 (y 2 + 2 y 3 + 3 2) + 4 3 2 – 24 = 0, (x + 4)2 – 4 (y + 3) 2 = 4 (: 4),
x 4 2 |
|
y 3 2 |
1 – каноническое уравнение гиперболы |
|
4 |
1 |
|||
|
[см. формулу (5)]. |
|||
|
|
|
Из уравнения видно, что центр гиперболы находится в точке (–4; –3), действительная полуось а = 2, мнимая полуось b = 1. Тогда эксцентриситет будет равен
|
ε |
c |
|
a2 b2 |
= |
22 12 |
|
5 |
1. |
|
|
a |
a |
2 |
2 |
|
|||||
|
|
|
|
|
|
|
||||
Так как c |
5 , то координаты фокусов равны F1; 2 -4 |
5; -3 . |
||||||||
Для построения гиперболы проведем вспомогательные оси через точку (-4; -3) (см. рисунок).
19

у
–6 |
–4 |
–2 |
0 |
х |
–2
–3
–4
Ответ: |
x 4 2 |
|
y 3 2 |
1. |
|
4 |
1 |
||||
|
|
|
|||
Задача 3. Даны координаты вершин пирамиды АBCD: |
|||||
А (0; –6; 2), |
B (2; –4; 2), |
C (8; 0; 0), D (1; 0; –2). Найдите: |
|||
1)уравнение высоты, опущенной из точки D на плоскость
АBC;
2)координаты проекции точки D на плоскость АBC.
Решение |
|
|
|
|
АBC по |
формуле (6); |
||||
1) |
Найдем уравнение плоскости |
|||||||||
А (0; –6; 2), B (2; –4; 2), |
C (8; 0; 0): |
|
|
|
|
|
||||
|
D |
|
x 0 |
y 6 |
z 2 |
|
||||
|
|
|
||||||||
|
|
2 0 |
4 ( 6) |
2 2 |
0 , или |
|||||
|
|
|
||||||||
|
|
|
8 0 |
0 ( 6) |
0 2 |
|
||||
B |
C |
|
|
|
|
|
|
|
|
|
D / |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
y 6 |
z 2 |
|
0 , или |
||
|
|
|
|
|
||||||
|
A |
|
2 |
2 |
0 |
|
|
|||
|
|
|
8 |
6 |
2 |
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
