|
2.4 Основные
уравнения движения электропривода
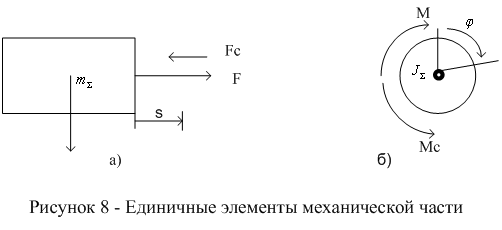
Рисунок
2.3 – Единичные элементы механической
части
Рассмотрим
единичный элемент, имеющий одну
степень свободы и совершающий только
поступательное или вращательное
движение. Мерой инерции будет масса
m,
кг, в первом случае или момент инерции
J,
кг·м2.
Массу будем считать сосредоточенной
в центре масс, а момент инерции
определять относительно оси вращения.
Движение
системы будет характеризоваться
координатами зависящими от времени:
линейным s(t)
или угловым φ(t)
перемещением;
линейной
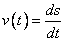 или
угловой скоростью или
угловой скоростью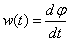 ; ;
линейным
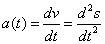 или
угловым или
угловым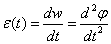 ускорением; ускорением;
иногда
используют третьи производные,
которые называют рывком (резкостью).
Во всех динамических режимах рывок
изменяется по закону близкому к
синусоидальному.
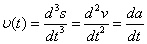 или или
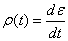
величина
обратная рывку называется плавностью
переходного процесса (П). Плавность
характеризует собой поведение
возмущающего момента. Если плавность
близка к нулю, то это значит, что
возмущающий момент на входном валу
изменяется скачкообразно, достигая
своего нового установившегося
значения за очень малое время.
Увеличение значения плавности
свидетельствует о том, что скорость
изменения момента в процессе его
приложения становиться всё меньше.
Отсутствие изменения момента на
входном валу соответствует бесконечно
большой плавности. Номинальные
значения плавности для а.д. с к.з.
ротором находятся в диапазоне П=(4 -
60)·10-6,
с3
Пусть
движение происходит под действием
сил F,
Н, приложенных к поступательно
движущейся массе, и моментов М, Н·м,
- к вращающейся массе. В общем случае
может быть много сил и моментов,
обусловленных разными причинами.
В
соответствии со вторым законом
Ньютона движение единичных элементов,
изображённых на рисунке 2.3
определиться соотношением
Для
поступательного движения
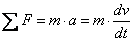 Для
вращательного движения
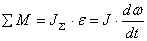
Масса
тела т
и
соответственно
момент инерции привода J
являются постоянными, что справедливо
для значительного числа производственных
механизмов.
Следовательно, уравнение равновесия
моментов действующих на механическую
систему запишется так Для
поступательного движения
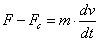 (2.10) (2.10) Для
вращательного движения
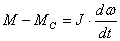 (2.11) (2.11) Уравнения
показывают, что развиваемый двигателем
вращающий момент М (или усилие
F)
уравновешивается моментом (или
силой) сопротивления на его валу
и инерционным, динамическим моментом
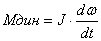 (или
усилием (или
усилием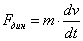 ) ) |
|
*
- Дополнительные разделы (для общего
развития) ©
Sens( o )R 2008 | (2.10) 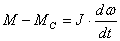 (2.11) (2.11)
1.
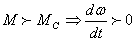  т.е.
состояние ускорения системы т.е.
состояние ускорения системы
(пуск,
разгон до большей скорости)
2.
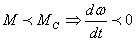 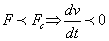 т.
е замедление т.
е замедление
(торможение
до меньшей скорости)
Условия
при которых
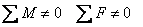 т.е
ускорения отличны от нуля, определяют
динамические (переходные режимы в
системе) т.е
ускорения отличны от нуля, определяют
динамические (переходные режимы в
системе)
3.
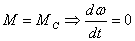 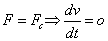 -
соответствуют установившемуся
режиму -
соответствуют установившемуся
режиму
(работа
с постоянной скоростью, или в частном
случае скорость равна нулю).
|
Знаки
всех моментов определяются в отношении
знака скорости вращения. Вращающийся
момент (сила), развиваемый двигателем
М (F)
при работе принимается положительным,
если он направлен в сторону движения
привода. Если в обратную сторону, то
принимается отрицательным.
Знак
минус перед МС
(Fс)
указывает на его тормозящее действие
при положительном знаке скорости,
что отвечает усилю резания, потерям
трения, подъему груза, сжатию пружины
и т. п. при положительном знаке
скорости. Т.е. положительное направление
момента сопротивления принимают
противоположным положительному
момента двигателя.
При
спуске груза, раскручивании или
разжатии пружины и т. п. перед Мс
(Fс)
ставится
знак плюс, поскольку в этих случаях
момент сопротивления помогает
вращению привода.
Инерционный
(динамический) момент (правая часть
уравнений 2.10
2.11)
проявляется только во время переходных
режимов, когда изменяется скорость
привода. При ускорении привода этот
момент направлен против движения,
а при торможении он поддерживает
движение. Инерционный момент как по
значению, так и по знаку определяется
алгебраической суммой моментов
двигателя и момента сопротивления.
При
учете сказанного о знаках моментов
формула 2.10
и 2.11
соответствует работе двигателя в
двигательном режиме при реактивном
моменте сопротивления (или при
потенциальном тормозящем моменте
сопротивления). В общем виде уравнение
движения привода может быть записано
следующим образом:
 (2.12) (2.12)
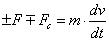 (2.13) (2.13)
Выбор
знаков перед значениями моментов и
сил в (2.12 и 2.13) зависит от режима
работы двигателя и характера моментов
сопротивления. |
|
*
- Дополнительные разделы (для общего
развития) ©
Sens( o )R 2008 |
|
2.5 Уравнение
движения привода при переменном
моменте инерции 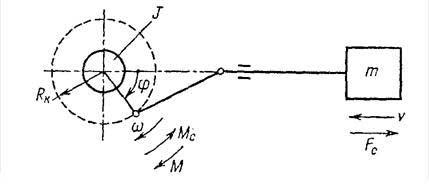
Рисунок
2.4 – Кривошипно – шатунный механизм
Переменный
момент инерции имеет место в
кривошипных механизмах, величина
момента инерции зависит от угла
поворота кривошипа J=f(φ). J
- представляет
собой суммарный приведенный к валу
двигателя момент инерции всех жестко
и линейно связанных вращающихся
элементов; т
- представляет
собой суммарную массу элементов,
жестко и линейно связанных с рабочим
органом механизма. Связь между
скоростями ω
и ν
нелинейная, причем ρ=ρ
(φ).
Запас
кинетической энергии системы

где
JΣ(φ)
– приведённый
к валу двигателя суммарный момент
инерции, зависящий от угла поворота
вала двигателя;
ω
-
угловая скорость двигателя
Динамическая
мощность
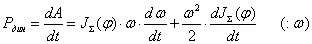 для
получения динамического момента для
получения динамического момента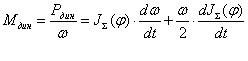
Т.к.
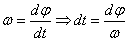 подставим
в предыдущее уравнение, в итоге
получаем подставим
в предыдущее уравнение, в итоге
получаем
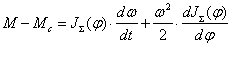 (2.14) (2.14)
Первое
слагаемое в уравнении 2.14 -
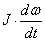 обусловлено
изменением скорости привода обусловлено
изменением скорости привода Второе
слагаемое
 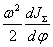 -
обусловлено изменением момента
инерции привода. -
обусловлено изменением момента
инерции привода. |
|
*
- Дополнительные разделы (для общего
развития) ©
Sens( o )R 2008 |
2.6
Механические характеристики
производственных механизмов и
электродвигателей
При
рассмотрении работы электродвигателя,
приводящего в действие производственный
механизм, необходимо выявить
соответствие механических характеристик
двигателя характеристике производственного
механизма. Зависимость
между приведенными к валу двигателя
скоростью и моментом сопротивления
механизма называют механической
характеристикой производственного
механизма ω
=
f
(Mc),
Mc=
f(ω).
Функция раскрывает свойства механизма,
т.е. показывает, какой момент возникает
в механизме если его приводить в
движение с различными скоростями
|
Различные
производственные механизмы обладают
различными механическими
характеристиками. Однако можно
получить некоторые обобщающие
выводы, если воспользоваться
следующей эмпирической формулой
для механической характеристики
производственного механизма:
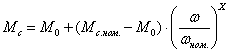
где
Мс
—
момент сопротивления производственного
механизма при скорости ω (статический
момент);
Мо
—
момент сопротивления трения в
движущихся частях механизма;
Mс.ном
— момент
сопротивления при номинальной
скорости ωном;
х
—
показатель степени, характеризующий
изменение момента сопротивления
при изменении скорости.
Приведенная
формула позволяет классифицировать
механические характеристики
производственных механизмов
ориентировочно на следующие основные
категории:

Рисунок
2.5 - Механические характеристики
производственных механизмов
1.
Не
зависящая от скорости
механическая характеристика
(прямая 1).
При этом х=0
и момент сопротивления Мс
не
зависит от скорости. Такой
характеристикой обладают, грузоподъёмные
механизмы, где момент сопротивления
движению создаётся, главным образом,
силой тяжести. Особенностью данной
характеристики является то, что
момент при подъеме груза несколько
превышает момент при спуске груза,
что связано с учётом механических
потерь в передачах. Характеристика
3 отвечает условиям работы машин,
где момент сопротивления определяется,
главным образом, силами трения
(транспортёры, конвейеры и др.машины).
В этом случае момент сопротивления
также не зависит от скорости механизма,
но при пуске механизма момент трения
покоя может существенно превышать
момент сил трения при движении.
2.
Зависящая
от знака скорости
механическая характеристика.
Характеристика (прямая 2) соответствует
машинам с рабочим органом резания,
нагрузка является реактивной. Не
зависит от величины скорости.
3.
Линейно
- возрастающая
механическая характеристика
(прямая 4).
В этом случае х
=
1 и момент сопротивления линейно
зависит от скорости ω, увеличиваясь
с ее возрастанием (для упрощения
принято Мо
=
0).
Такая
характеристика получится, например,
в приводе генератора постоянного
тока с независимым возбуждением,
если последний будет работать на
постоянный внешний резистор.
4.
Нелинейно-возрастающая
(параболическая)
механическая характеристика (кривая
5).
Этой характеристике соответствует
х=2;
момент сопротивления Мс
здесь
зависит от квадрата скорости.
Механизмы, обладающие такой
характеристикой, называют иногда
механизмами с вентиляторным
моментом, поскольку у вентиляторов
момент сопротивления зависит от
квадрата скорости. К механизмам,
обладающим параболической механической
характеристикой, относятся также
центробежные насосы, гребные
винты и т. п. Показатель степени может
быть х>2,
например, для центробежных насосов,
работающих на противодавление.
5.
Нелинейно-спадающая
механическая
характеристика (кривая 6).
При этом х=-1
и момент сопротивления Мс
изменяется
обратно пропорционально скорости,
а мощность, потребляемая механизмом,
остается постоянной. Такой
характеристикой обладают, например,
некоторые токарные, расточные,
фрезерные и другие металлорежущие
станки, моталки в металлургической
промышленности и т. п.
6.
Механическая характеристика,
являющаяся периодической
функцией угла поворота рабочего
органа механизма.
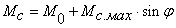
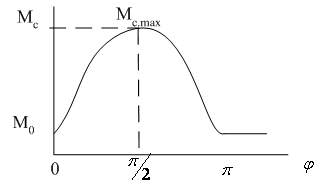
Рисунок
2.6 – механическая характеристика в
функции угла поворота Такие
нагрузки можно представить, если
например при резании заготовка имеет
в сечении овальную форму. Появление
периодических нагрузок могут вызывать
нелинейные кинематические связи
типа кривошипно–шатунных, кулисных
и других механизмов, у которых
периодической функцией угла поворота
двигателя является радиус приведения. |
|
*
- Дополнительные разделы (для общего
развития) ©
Sens( o )R 2008 |
Приведённые
механические характеристики
производственных механизмов позволяют
оценить, какую нагрузку будет нести
электродвигатель в установившемся
режиме при различных угловых скоростях,
которые необходимо задавать механизму
с целью регулирования его производительности
в соответствии с изменяющимися
технологическими условиями.
Механической
характеристикой электродвигателя
называется зависимость его угловой
скорости ω
или частоты вращения (n)
от вращающего момента, т.е. ω=f(М).
Почти
все электродвигатели обладают тем
свойством, что скорость их является
убывающей функцией момента двигателя.
Так как в установившемся режиме М=Мс,
поэтому механическая характеристика
двигателя даёт представление о том,
как изменяется скорость двигателя от
нагрузки на его валу. ω=f(М).
Почти
все электродвигатели обладают тем
свойством, что скорость их является
убывающей функцией момента двигателя.
Так как в установившемся режиме М=Мс,
поэтому механическая характеристика
двигателя даёт представление о том,
как изменяется скорость двигателя от
нагрузки на его валу.
|
|
|
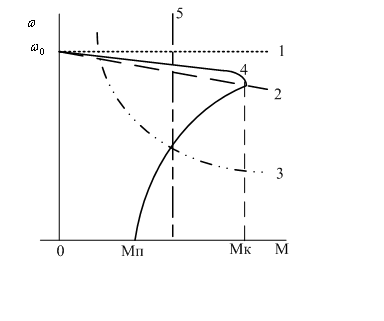
Рисунок
2.7 - Механические характеристики
двигателей | Механические
характеристики двигателей подразделяются
на
естественные - когда
двигатель подключается к номинальному
напряжению сети без добавочных
сопротивлений в цепи якоря, ротора
или статора.
Характеристики,
получаемые при изменении какого –
либо параметра двигателя (U,
f,
Ф, Rдоб),
называются искусственными.
Эти характеристики служат для получения
различных скоростей вращения в
установившемся режиме, а также для
ограничения тока, момента, ускорения
и т.п. в переходные режимы.
Степень
изменения скорости с изменением
момента у разных двигателей различна
и характеризуется так называемой
жесткостью их механических характеристик.
Жесткость механической характеристики
электропривода — это отношение
разности электромагнитных моментов,
развиваемых электродвигательным
устройством, к соответствующей разности
угловых скоростей электропривода, т.
е.
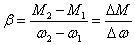
Обычно
на рабочих участках механические
характеристики двигателей имеют
отрицательную жесткость β<0.
Линейные механические характеристики
обладают постоянной жесткостью. В
случае нелинейных характеристик их
жесткость не постоянна и определяется
в каждой точке как производная момента
по угловой скорости
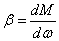
Понятие
жесткости может быть применено и к
механическим характеристикам
производственных механизмов. Эти
характеристики можно оценивать
жесткостью
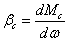
|
|
|
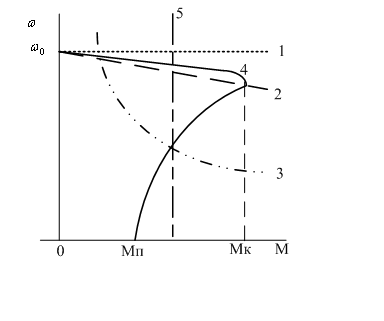
Рисунок
2.7 - Механические характеристики
двигателей | Механические
характеристики электродвигателей по
степени жёсткости можно разделить на
четыре основные категории:
1.Абсолютно
жесткая механическая характеристика
(β=∞) — это характеристика, при которой
скорость с изменением момента остается
неизменной. Такой характеристикой
обладают синхронные двигатели (прямая
1, рис.2.7).
2.
Жесткая
механическая характеристика
— это характеристика, при которой
скорость с изменением момента хотя и
уменьшается, но в малой степени. Жесткой
механической характеристикой обладают
двигатели постоянного тока независимого
возбуждения, а также асинхронные
двигатели в пределах рабочей части
механической характеристики (кривая
2 и линейный участок характеристики
4, рис. 2.7).
3.
Мягкая
механическая характеристика
— это характеристика, при которой с
изменением момента скорость значительно
изменяется. Такой характеристикой
обладают двигатели постоянного тока
последовательного возбуждения,
особенно в зоне малых моментов (кривая
3
на
рис. 2.7). Для этих двигателей жесткость
не остается постоянной для всех точек
характеристик.
Двигатели
постоянного тока смешанного возбуждения
могут быть отнесены ко второй или
третьей группе в зависимости от
значения жесткости механической
характеристики.
4.
Абсолютно
мягкая механическая характеристика
(β=0)
- это характеристика, при которой
момент двигателя с изменением угловой
скорости остается неизменным. Такой
характеристикой обладают, например,
двигатели постоянного тока независимого
возбуждения при питании их от источника
тока или при работе в замкнутых системах
электропривода в режиме стабилизации
тока якоря (прямая 5
на
рис.2.7).
2.7
Установившийся режим работы
электропривода
|

|
|
Рисунок
2.8 – Режимы работы электродвигателей | Механические
характеристики позволяют просто и
наглядно определить координаты
установившегося (статического) режима.
Работе
электрического двигателя и
производственного механизма в
установившемся режиме соответствует
равновесие момента сопротивления
механизма и вращающего момента
двигателя т. е. М=Мс.
Тогда скорость установившегося режима
определяется, как ордината пересечения
характеристик двигателя и производственного
механизма.
Оси
координат разделяют поле на четыре
квадранта. Любая точка I
и III
квадрантов соответствует двигательному
режиму работы электрической машины
(за исключением осей координат). При
этом мощность машины Р>0 и электрическая
энергия преобразуется в механическую.
Точки квадрантов II
и IV,
соответствуют генераторному режиму
работы электрической машины Р<0. В
этом случае двигатель преобразует
механическую энергию в электрическую,
развивая тормозной момент. Генераторный
режим работы двигателя является
режимом электрического торможения
Генераторных
режимов может быть несколько в
зависимости от того, как используется
преобразованная электрическая энергия.
Классификация следующая:
1.
Генераторный режим с отдачей энергии
в сеть — режим
рекуперативного торможения. В этом
случае преобразованная электрическая
энергия за вычетом потерь отдается
машиной в сеть. Баланс мощностей
выражается следующим образом:
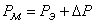
где
Рм
-
механическая мощность на валу двигателя;
Рэ
— электрическая
мощность, поступающая в сеть;
ΔР
—
результирующая мощность потерь в
силовых цепях
двигателя.
Переход
из двигательного режима в режим
рекуперативного
торможения возможен при увеличении
скорости двигателя
сверх скорости идеального холостого
хода, когда
М
=
0. Получение тормозного момента в
двигателе
с одновременной отдачей им энергии в
сеть позволяет считать данный режим
торможения как экономичный.
2.
Режим торможения противовключением.
В этом случае
электрическая машина потребляет как
механическую
энергию с вала, так и электрическую
энергию из сети.
Суммарная энергия расходуется в
силовых цепях двигателя, т. е.
PM
+Pэ
= ΔP.
Этот
режим характеризуется большими
электрическими потерями.
3.
Режим
динамического торможения. В этом
случае на потери в силовой цепи
двигателя расходуется только
преобразованная
электрическая энергия. Энергию из
сети машина
не получает, т. е.
Рм=ΔР.
Для
осуществления данного режима двигатель
обычно отключают
от сети и в его силовую цепь вводят
дополнительное
сопротивление. В отдельных случаях
электрическая
машина, подключенная к питающей сети,
может не
обмениваться с ней активной мощностью,
а
потреблять механическую мощность с
вала и преобразовывать ее в потери,
т. е. также работать в режиме динамического
торможения.
Граничные
режимы, отделяющие двигательные режимы
от генераторных, соответствуют
определенным точкам на координатных
осях. Там, где М
= 0
при
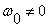 ,имеет
место идеальный холостой ход двигателя.
Чтобы машина могла работать в данном
режиме,
требуется к ее валу подвести небольшую
мощность, компенсирующую механические
потери. При ω0=0
и ,имеет
место идеальный холостой ход двигателя.
Чтобы машина могла работать в данном
режиме,
требуется к ее валу подвести небольшую
мощность, компенсирующую механические
потери. При ω0=0
и
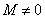 имеетместо
так называемый режим короткого
замыкания. В
этом случае механическая мощность
равна нулю, а потребляемая из сети
электрическая энергия полностью
расходуется на потери. имеетместо
так называемый режим короткого
замыкания. В
этом случае механическая мощность
равна нулю, а потребляемая из сети
электрическая энергия полностью
расходуется на потери.
Изменение
момента сопротивления на валу двигателя
приводит к тому, что скорость двигателя
и момент, который он развивает, могут
автоматически изменяться, и привод
будет продолжать устойчиво работать
при другой скорости с новым значением
момента.
Для
восстановления равновесия между
изменившимся моментом сопротивления
и моментом двигателя во всех
неэлектрических двигателях требуется
участие специальных регуляторов,
которые воздействуют на источник
энергии, увеличивая или соответственно
уменьшая подачу воды, топлива или
пара. В электрических двигателях роль
автоматического регулятора может
выполнять ЭДС двигателя. Эта
особенность электродвигателей
автоматически поддерживать равновесие
системы при изменяющемся моменте
сопротивления является весьма ценным
свойством.
|
|
|
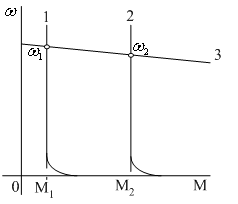
Рисунок
2.9 – Характеристики двигателя
и механизма |
|
Начало
формы
Конец
формы | На
рисунке приведены механическая
характеристика 3
двигателя
постоянного тока независимого
возбуждения и две характеристики 1 и
2
производственного
механизма, например конвейера,
приводимого в движение этим двигателем.
Механические характеристики
производственного механизма для
удобства изображаются в первом
квадранте, хотя момент сопротивления
имеет отрицательное значение (для
принятого положительного направления
моментов)
Характеристика
1
соответствует
моменту сопротивления М1
при
холостом ходе конвейера. Характеристика
2
получается
при большом моменте сопротивления М2
после,
того, как на конвейер положены
транспортируемые им детали. Вначале
при холостом ходе конвейера М
=
M1
двигатель
работает со скоростью ω1.
С увеличением нагрузки двигатель
тормозится, скорость его снижается,
благодаря чему уменьшается ЭДС. При
уменьшении ЭДС возрастают ток в якорной
цепи двигателя и момент, развиваемый
двигателем. Рост момента двигателя
продолжается до тех пор, пока не
наступит равновесие моментов М
=
М2
(точка
ω2).
Эта новая точка также является общей
для механической характеристики
конвейера (2)
и
механической характеристики
электродвигателя (3). Для лучшего
усвоения посмотрите демонстрацию.
Рассмотренные
условия работы электропривода в
установившемся режиме характеризуют
статическую устойчивость привода,
когда изменение во времени скорости
и момента происходит относительно
медленно в отличие от динамической
устойчивости, имеющей место при
переходных режимах.
2.8
Статическая устойчивость ЭП
Механические
характеристики двигателей и
производственных механизмов должны
подбираться так, чтобы обеспечивать
устойчивую работу привода в установившемся
режиме.
В
статически
устойчивой системе при случайно
возникшем отклонении скорости от
установившегося значения привод
возвратится в точку установившегося
режима. При неустойчивом
движении любое, даже самое малое,
отклонение скорости от установившегося
значения приводит к изменению состояния
привода — он не возвращается в точку
установившегося режима.
Привод
статически устойчив, если в точке
установившегося режима выполняется
условие
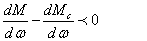 или или
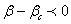
Данное
условие означает, что привод статически
устойчив, если при положительном
приращении угловой скорости момент
двигателя окажется меньше статического
момента (момента сопротивления) и
привод вследствие этого затормозится,
до прежнего значения скорости. При
отрицательном приращении угловой
скорости момент двигателя окажется
больше момента сопротивления и привод
вследствие этого разгонится до прежнего
значения скорости.
При
постоянном моменте нагрузки статическая
устойчивость будет определяться
только жесткостью механической
характеристики двигателя, так как
dMс/dω=
0.
Если она отрицательна, то работа
в установившемся режиме устойчива.
|
|
|
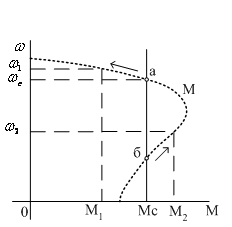
Рисунок
2.10 – Определение
устойчивости
привода |
|
Начало
формы
Конец
формы | Для
т.а – устойчива
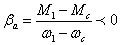 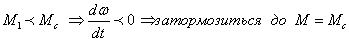
Для
т.б – неустойчива
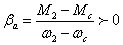 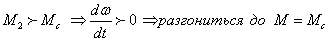
При
работе того же двигателя на механизм
с вентиляторной характеристикой
легко доказать, что во всех точках
работа будет устойчивой. Для лучшего
усвоения материала посмотрите
демонстрацию
Обычно
при проектировании электропривода
механическая характеристика
производственного механизма является
уже заданной. Поэтому для получения
устойчивой работы в установившемся
режиме для определенных скоростей
и моментов сопротивления производственных
механизмов необходимо подбирать
механическую характеристику
электродвигателя соответствующей
формы. Это может быть достигнуто
подбором электродвигателя
соответствующего типа и изменением
электрических параметров его цепей.
Иногда для получения требуемых
механических характеристик приходится
применять специальные схемы включения
электрических машин и аппаратов.
2.9
Переходные режимы работы ЭП
Переходным
режимом электропривода называют
режим работы при переходе от одного
установившегося состояния к другому,
когда изменяются скорость, момент и
ток.
Причинами
возникновения переходных режимов в
электроприводах является: либо
изменение нагрузки, связанное с
производственным процессом, либо
воздействие на электропривод при
управлении им, т.е. пуск, торможение,
изменение направления вращения и т.
п. Переходные режимы в электроприводах
могут возникнуть также в результате
аварий или нарушения нормальных
условий электроснабжения (например,
изменения напряжения или частоты
сети, несимметрия напряжения и т. п.).
Характерной
чертой переходных режимов является
возникновение динамических составляющих
момента, тока, мощности и т.п., что
связано с дополнительной нагрузкой
двигателя, его перегревом. Быстрое
протекание переходных процессов
может привести к недопустимым
перегрузкам, ударам в механической
части. Медленное
протекание переходных процессов
приводит к снижению производительности. Анализ
переходных процессов позволяет
1.
Установить характер изменения скорости,
моментов токов и т.д.
2.
Определить длительность переходных
процессов
3.
Определить потери в двигателе, его
нагрев. При
учёте этих факторов можно разработать
систему электропривода, обеспечивающую
максимальную производительность и
безаварийную работу. Переходный
процесс происходит во времени, причинами
немгновенности переходного процесса
являются
1.
Механическая инерционность,
обусловленная изменением скорости
(пуск, торможение, реверс.)
2.
Электромагнитная инерционность,
обусловленная изменением тока в
обмотках двигателя.
3.
Тепловая инерционность, обусловленная
нагреванием всех частей двигателя. Для
оценки степени влияния каждого вида
инерционности на переходный процесс
вводится понятие постоянной времени.
Электромеханическая
постоянная
-
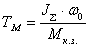 ,
с. ,
с.
Это
время в течение, которого, привод
разогнался бы вхолостую (Мс=0)
до скорости 0,
под действием момента Мк.з.
Электромагнитная
постоянная -
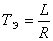 ,
с ,
с
Постоянная
нагрева -
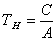 ,
с. ,
с.
Это
время, в течение которого двигатель
нагрелся бы до установившейся
температуры при отсутствии теплоотдачи
в окружающую среду.
где
С
-
теплоёмкость, Дж/град,
А
- коэффициент теплоотдачи, Дж/сград.
В
зависимости от требуемой точности
расчёт переходных процессов производят
как с учётом ТМ
- электромеханические процессы, так
и с учётом ТЭ
- электромагнитные процессы.
2.10
Время ускорения и замедления привода
Поскольку
периоды разгона и торможения ЭП обычно
снижают эффективность работы механизма,
их стремятся сокращать. Особенно важно
такое сокращение для приводов
механизмов, работающих с частыми
пусками, остановками, реверсами.
Решим
уравнение движения ЭП, разделяя
переменные, получим время t12
для изменения скорости от нач
до
кон.
Для решения этого интеграла необходимо
знать зависимость моментов двигателя
и механизма от скорости. В простейшем
случае, приняв Мс=const,
М=const,
J=const
получаем.
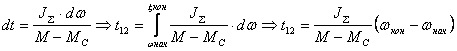 (2.15) (2.15)
Если
обозначить пусковой момент двигателя
за Мп
= км·Мн,
где
км
– коэффициент перегрузочной способности
двигателя (1.8÷2.5)
Мн
– номинальный момент машины.
то
время пуска при изменении скорости
от 0 до Н,
соответствующей
нагрузке на валу буде равно
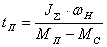 (2.16) (2.16)
Из
(2.15) видно, что теоретически полное
время переходного процесса равно
бесконечности. Действительно, поскольку
переходный процесс заканчивается при
наступлении равенства моментов
(М=Мс),
то величина, стоящая под знаком
интеграла, стремится к бесконечности.
В практических расчетах обычно
считают, что процесс разбега
заканчивается
при скорости, равной не ωкон,
а
приблизительно
ω=
0,95 ωкон
тогда время разбега получит конечное
значение. В
тех случаях, когда динамический момент
имеет отрицательное значение, привод
замедляется, уравнение моментов имеет
вид
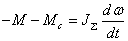 (2.17) (2.17) Очевидно,
что электрический привод замедляется
и в том случае, когда двигатель развивает
момент положительный по абсолютному
значению, но меньше чем момент
сопротивления
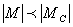 Из
уравнения движения привода следует,
что время торможения 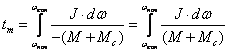
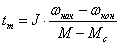 (2.18) (2.18)
Пользуясь
данным уравнением можно определить
время торможения до остановки привода
при моменте двигателя равном тормозному
Мт=кмМн
Данные
расчёта можно изобразить графически

Рисунок
2.11 – Диаграмма пуска и торможения
При
М=0 скорость двигателя равна скорости
идеального холостого хода ω0.
Тогда время разгона
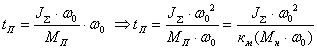
Следовательно,
при заданной мощности двигателя и
перегрузочной способности, время
разгона пропорционально запасу
кинетической энергии вращающихся
частей. В режиме частых пусков и
остановок необходимо выбирать двигатель
с меньшим запасом кинетической энергии,
при этом уменьшается не только время,
но и потери энергии в переходных
режимах
В
электроприводе, представляющем собой
жёсткое приведённое звено (одномассовая
система) при М
= const
и Мс
= const
в соответствии с уравнением
движения, ускорение
электропривода
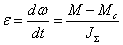 также
постоянно. также
постоянно.
Движение
электропривода при
М
≠ Мс
может
быть равноускоренным или равнозамедленным.
Чем больше масса, тем медленнее
изменяется скорость как двигателя,
так и любого другого движущегося
элемента механической части привода.
Если
механическое звено содержит редуктор,
то при изменении его передаточного
отношения ip
изменяется и соотношение между
скоростями и ускорениями двигателя
и рабочего органа производственного
механизма. Можно найти такое значение
ip,
при
котором ускорение на рабочем органе
будет наибольшим для одних и тех же
двигателя и производственного
механизма. Пренебрегая потерями в
передачах (η=1),
уравнение движения можно записать
относительно рабочего органа механизма
в виде

где
Мс.м,
Jм,
ωм—
соответственно момент нагрузки, момент
инерции и угловая скорость механизма.
к
– учитывающий момент инерции передач.
Минимальное
время разгона имеет место при наибольшем
ускорении.
Решая
это уравнение относительно ускорения
на рабочем органе, получаем
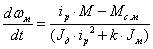
Пользуясь
правилом определения максимума dωм/dt
и
полагая, Мс=const,
а также М
= const
(средним за период переходного режима),
находим оптимальное (или наивыгоднейшее)
передаточное отношение iр
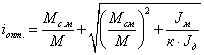
В
том случае, когда момент сопротивления
оказывается значительно меньшим
момента двигателя при пуске и торможении
 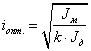 3.
Электропривод постоянного тока
Двигатели
постоянного тока традиционно являлись
основой регулируемого электропривода
и широко применяются во всех областях
техники. Только в последние годы
началось интенсивное использование
регулируемых электроприводов на базе
двигателей переменного тока.
Двигатели
постоянного тока могут иметь независимое,
параллельное, последовательное
или смешанное возбуждение. В зависимости
от схемы возбуждения существенно
отличаются и электромеханические
характеристики двигателей. 3.1 Характеристики
двигателя постоянного тока с независимым
(параллельным) возбуждением 3.1.1
Способы исполнения двигателей
постоянного тока с независимым
возбуждением (ДПТНВ)
Двигатели
независимого возбуждения могут иметь
электромагнитное возбуждение,
(рис.3.1,б) и возбуждение от постоянных
магнитов (рис.3.1,а), Последнее применяется
для высокодинамичных двигателей
мощностью
до 20 кВт. Данные двигатели
называются высокомоментными двигателями
постоянного тока. (серии ДК1, ПБВ)
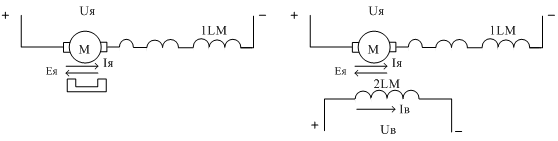
а)
б) Рисунок
3.1 – Схема включения двигателя
постоянного тока с возбуждением от
постоянных магнитов (а), с электромагнитным
возбуждением (б)
Благодаря
применению постоянных магнитов на
основе редкоземельных элементов
(например, сплава самарий-кобальт),
эти двигатели особенно при малых
скоростях вращения способны развивать
большой крутящий момент. Отношение
пускового момента такого двигателя
к номинальному составляет 8-10, в то
время как у двигателей с электромагнитным
возбуждением это отношение не превышает
2-4. Двигатели находят применение в
металлорежущих станках с числовым
программным управлением, в приводах
роботов и следящих электроприводах
различного назначения.
В
некоторых случаях двигатели независимого
возбуждения снабжают «легкой,
стабилизирующей» обмоткой
последовательного возбуждения,
создающей м.д.с. при номинальном токе
якоря около 20% от м.д.с. обмотки
независимого возбуждения. Высокодинамичные
двигатели смешанного возбуждения
применяются в случаях многодвигательного
привода, когда два или несколько
двигателей работают на один вал или
их валы связаны механически (например,
лентой конвейера), В этом случае
скорость всех двигателей будет
одинаковой, но из-за неидентичности
характеристик двигателя возникает
задача равномерного распределения
нагрузки между ними. Благодаря
наличию последовательной обмотки
возбуждения в более нагруженном
двигателе увеличивается поток
и возрастает противо э.д.с. якоря,
что ведет к снижению тока якоря.
Напротив, менее нагруженный
двигатель будет иметь несколько
меньший
поток,
его э.д.с. будет ниже и ток якоря
соответственно возрастает. Таким
образом, благодаря наличию слабой
последовательной обмотки происходит
выравнивание тока якоря между
двигателями, питающимися от общего
источника напряжения.
Для
устранения размагничивающего
действия реакции якоря на крупных
машинах используют компенсационную
обмотку, которая включается
последовательно с обмоткой якоря и
располагается на полюсах машины,
усиливая поток возбуждения. 3.1.2
Основные уравнения для ДПТНВ
Напряжение,
подводимое к якорной цепи двигателя,
в установившемся режиме уравновешивается
падением напряжения на сопротивлениях
цепи якоря и противо э.д.с. якоря,
которая наводится в обмотке якоря
при его вращении в электромагнитном
поле, создаваемом обмоткой возбуждения
(см.рис.3.1,а)
Uя=Eя+RяIя,
(3.1)
где
Rя
-
сопротивление якорной цепи, складывающееся
из сопротивления обмотки якоря
Rо.я,
обмотки дополнительных полюсов
Rдn,
компенсационной
обмотки Rк.о
(если
она имеется) и сопротивление
стабилизирующей обмотки Rс.о
(если
она имеется)
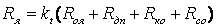 ,
(3.2) ,
(3.2)
где
кt
– коэффициент
приведения
температуры обмоток якорной цепи к
рабочей температуре t
= 75°C.
кt=1,24
для
двигателей до 100 кВт; кt=1,32
для
двигателей большей мощности.
Э.д.с.
якоря Ея
равна
Ея
=
к·Ф
·ω,
(3.3)
где
Ф
-
поток возбуждения (Вб);
к
= p·N
/2πа -
конструктивная постоянная двигателя;
где
р
- число
пар полюсов машины;
N
- число активных проводников обмотки
якоря;
а
–
число пар параллельных ветвей обмотки
якоря.
Момент,
развиваемый двигателем, пропорционален
току якоря и потоку возбуждения
М=кФIя,
(3.4)
Решая
уравнение 3.1 относительно скорости
получаем зависимость скорости от тока
якоря ω = f(Iя),
которая называется электромеханической
(скоростной) характеристикой двигателя
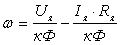 .
(3.5) .
(3.5)
Выражая
ток якоря из 3.4 и подставляя в уравнение
3.5 получаем зависимость скорости
от момента двигателя ω
=
f(M)
-
механическую характеристику
привода.
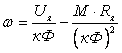 .
(3.6) .
(3.6)
Если
двигатель во всех режимах работает с
постоянным номинальным потоком
возбуждения, то величину считают
постоянной, кФн=С.
Величину
кФн
можно
определить по паспортным данным
двигателя
из
уравнения 3.3 или 3.4
по
формулам
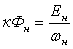 ;
(3.7) ;
(3.7)
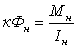 .
(3.8) .
(3.8) 3.2
Построение естественных характеристик
двигателя по паспортным данным 3.2.1
Построение механической характеристики
Естественная
механическая и скоростная
характеристики двигателя постоянного
тока независимого возбуждения имеют
вид прямых, пересекающих ось ординат,
поэтому они могут быть построены по
двум точкам. Эти две точки для каждой
характеристики могут быть любыми,
однако построение естественной
характеристики удобнее производить
по точкам одна из которых соответствует
номинальному электромагнитному
моменту и номинальной скорости, а
другая – скорости идеального холостого
хода.
Дано:
Uн,
Pн,
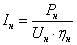 ,nн,
ηн, ,nн,
ηн,
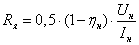 . .
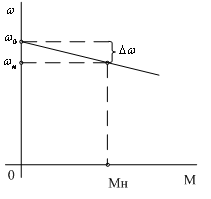
Рисунок
3.2 - Механическая характеристика ДПТНВ
1
точка – в уравнении 3.5 или 3.6 М=0, угловая
скорость в этой точке ω0
имеет определённое значение и называется
скоростью идеального холостого хода:
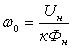 .
(3.9) .
(3.9)
2
точка – номинальный режим работы
привода ωн,
Мн 3.2.2
Построение динамических характеристик
При
скорости идеального холостого хода,
когда ток в якорной цепи равен нулю,
ЭДС якоря, направленная навстречу
приложенному
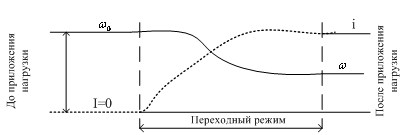
Рисунок
3.3 - Динамическая характеристика при
приложении нагрузки
напряжению,
равна ему по абсолютному значению.
Если двигатель до приложения нагрузки
работал с угловой скоростью ω0,
то при появлении на его валу момента
сопротивления в соответствии с
уравнением движения привода
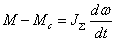
угловая
скорость будет снижаться. Следствием
этого будет уменьшение ЭДС вращения
Е
согласно
(3.3) и увеличение тока якоря
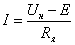 (в
соответствии с 3.1) (в
соответствии с 3.1)
и
момента двигателя по (3.4). Угловая
скорость будет снижаться до тех пор,
пока момент двигателя не сравняется
с моментом сопротивления. Разность
значений установившихся скоростей
электропривода до и после приложения
заданной статической нагрузки
называется статическим падением
(перепадом) скорости электропривода
Δω.
Второй
член (3.5, 3.6) характеризует собой
статическое падение угловой скорости
(перепад) относительно угловой скорости
идеального холостого хода
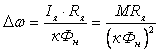 .
(3.10) .
(3.10)
Таким
образом, уравнение для скорости
двигателя может быть записано так
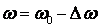 .
(3.11) .
(3.11)
Кроме
того, вторые члены уравнений характеризуют
наклон характеристики к оси абсцисс,
который зависит от суммарного
сопротивления в якорной цепи и величины
магнитного потока. Учитывая, что
сопротивление в якорной цепи можно
только увеличивать, а магнитный поток
только уменьшать, то увеличение
Rя
и уменьшение основного магнитного
потока Фн,
приводит к увеличению наклона
характеристики к оси абсцисс. 3.2.3
Понятие жесткости характеристик
В
теории электропривода для оценки
изменения скорости вращения при одних
и тех же значениях тока
I
и момента М
вводится понятие жёсткости характеристик
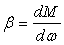 .
(3.12) .
(3.12)
Из
уравнения механической получаем
выражение жёсткости для двигателя
постоянного тока независимого
возбуждения
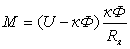 ; ;
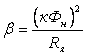 .
(3.13) .
(3.13)
Наибольшую
жёсткость имеет естественная,
механическая характеристика, её
уравнение с учётом жёсткости можно
записать в следующем виде
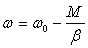 .
(3.14) .
(3.14) 3.3
Уравнение характеристик двигателя в
относительных единицах
Для
сравнения характеристик двигателей
различной мощности удобно представить
характеристики двигателя в относительных
единицах. При этом принимаются следующие
базисные величины:
Uб=Uн,
Iб=Iн,
Фб=Фн
-
номинальные значения напряжения, тока
якоря и потока возбуждения. Тогда в
относительных величинах
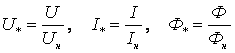 , ,
ωб
=
ω0е
– скорость идеального холостого хода
на естественной характеристике;
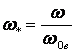 -
относительное значение скорости; -
относительное значение скорости;
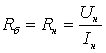
– номинальным
сопротивлением двигателя постоянного
тока называется такое сопротивление,
которое при неподвижном якоре и
номинальном напряжении ограничивает
ток в якоре номинальным значением,
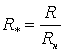 ; ;
Мб
=
Мн
– номинальный электромагнитный момент
, ; ;
Рб
=
Uн·Iн
– мощность,
потребляемая двигателем из сети в
номинальном режиме,
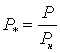 ; ;
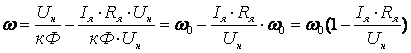
разделим
левую и правую часть на ω0;
Уравнение
скоростной
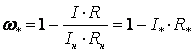 ; ;
и
соответственно, механической
характеристики
при Ф=Фн=const:
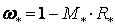 . .
Второй
член правой части представляет собой
перепад угловой скорости, выраженный
в относительных единицах и равный
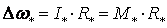 .
(3.15) .
(3.15)
Последнее
равенство позволяет при известных
условиях значительно упростить расчет
механических характеристик.
Действительно, если рассматривать
точки механических характеристик,
отвечающие номинальному моменту, то
для них
I*
= 1 и М*
= 1
и,
следовательно, равенство принимает
вид
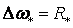 .
Это
означает, что при номинальном моменте
относительный перепад угловой
скорости двигателя численно равен
относительному сопротивлению якорной
цепи двигателя. .
Это
означает, что при номинальном моменте
относительный перепад угловой
скорости двигателя численно равен
относительному сопротивлению якорной
цепи двигателя. 3.4
Основные показатели регулирования
угловой скорости электроприводов
Регулированием
скорости называется принудительное
изменение скорости электропривода в
зависимости от требований
технологического процесса. Понятие
регулирования скорости не следует
смешивать с естественным изменением
скорости, возникающим в электроприводах
в силу изменения нагрузки на валу
работающей машины. Регулирование
скорости осуществляется дополнительным
воздействием на приводной двигатель;
оно может быть произведено человеком
или специальным автоматическим
устройством.
В
настоящее время все большее применение
находит электрическое регулирование
скорости, которое имеет ряд преимуществ
в отношении технических и экономических
показателей.
1.
Диапазон
регулирования угловой скорости
определяется
отношением возможных установившихся
скоростей максимальной ωтах
к
минимальной ωmin
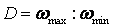 , ,
при
заданной точности регулирования (с
заданным статическим падением
скорости электропривода) для
установленных пределов изменения
момента нагрузки и других возмущений.
Обычно
диапазон регулирования выражается в
числах в виде отношения, например:
2:1, 4:1, 10:1, 20:1 и т. д. Современные системы
автоматического регулирования
электроприводов с обратными связями
позволяют существенно расширить
диапазон регулирования скорости.
Различные
производственные машины требуют
разных диапазонов регулирования.
Например, главные механизмы металлорежущих
станков в зависимости от их назначения
работают с диапазонами регулирования
D
— (4
: 1) ÷(100 : 1) и выше; для механизмов подач
универсальных станков требуется
диапазон до 10 000 : 1 и выше. От двигателя
требуется возможно больший диапазон
регулирования. Однако имеются
ограничения по верхней и нижней
скорости вращения. Верхняя скорость
вращения ограничена условиями
механической прочности ротора и самого
механизма. Нижний диапазон ограничен
точностью поддержания скорости
вращения из-за снижения жёсткости
механических характеристик.
2.
Плавность
регулирования характеризует
скачок скорости при переходе от
данной скорости к ближайшей возможной.
Плавность тем выше, чем меньше этот
скачок. Число скоростей, получаемых
в данном диапазоне, определяется
плавностью регулирования. Ее можно
оценить коэффициентом плавности
регулирования, который находится как
отношение двух соседних значений
угловых скоростей при регулировании
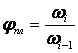 , ,
где
ωi
ωi-1
угловые скорости соответственно на
i-й
и (i-1)-й
ступенях регулирования.
При
плавном регулировании
φпл→
1, а число скоростей z→
∞. В случае ступенчатого регулирования
коэффициент плавности регулирования
может существенно отличаться от
единицы. Число скоростей, диапазон
регулирования D
и
коэффициент плавности регулирования
при таком регулировании связаны
между собой равенством
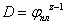 , ,
4.
Стабильность
угловой скорости характеризуется
изменением угловой скорости при
заданном отклонении момента нагрузки
и зависит от жесткости
механической
характеристики; она тем выше, чем
больше жесткость характеристики.
5.
Направление регулирования скорости,
т.
е. уменьшение или увеличение ее по
отношению к основной скорости, зависит
от способов регулирования. Основная
угловая скорость, например, двигателя
постоянного тока независимого
возбуждения соответствует номинальным
значениям напряжения и магнитного
потока.
Различают
однозонное регулирование вниз от
основной скорости, однозонное
регулирование вверх от основной
скорости и двухзонное регулирование,
когда имеется возможность получать
характеристики выше и ниже естественной.
6.
Допустимая
нагрузка двигателя, т.
е. наибольшее значение момента, который
двигатель способен развивать длительно
при работе на регулировочных
характеристиках, определяется нагревом
двигателя и для разных способов
регулирования будет различной.
скорости. Однако в таком случае
регулирование угловой скорости
двигателя может оказаться неэкономичным,
так как двигатель на разных угловых
скоростях будет использован
неодинаково и при работе на некоторых
из них будет недогружен.
Недогрузка
двигателя ведет к ухудшению
эксплуатационных показателей
привода, так как при этом уменьшается
КПД двигателя, а при переменном токе,
кроме того, уменьшается и коэффициент
мощности. Желательно поэтому применять
такой способ регулирования, при
котором двигатель был бы по
возможности полностью загружен
при всех угловых скоростях.
Допустимая
нагрузка двигателя ограничивается
степенью его нагрева. Степень
нагрева в свою очередь зависит от
потерь энергии в двигателе, а последние
определяются главным образом током,
потребляемым двигателем.
Таким
образом, условием полного использования
двигателя при работе на разных
регулировочных характеристиках
является постоянство нагрузочного
тока. Если при работе на всех
характеристиках ток будет равен
номинальному току двигателя, то это
и будет означать, что двигатель загружен
полностью при всех угловых скоростях.
Тогда допустимый момент, например,
двигателя постоянного тока
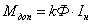 зависит
от способа регулирования. зависит
от способа регулирования. 3.5
Регулирование скорости ДПТ НВ
Из
уравнения скоростной или механической
характеристик, вытекает, что возможны
три способа регулирования угловой
скорости двигателя
1)
Изменением напряжения на якоре
2)
Изменением сопротивления цепи якоря
3)
Изменением тока возбуждения.
|
3.5.1
Регулирование угловой скорости
двигателей постоянного тока с
независимым возбуждением при введении
сопротивления в якорную цепь
3.5.1.1
Реостатное регулирование
Схема
включения двигателя представлена
на рисунке 3.4 Регулирование скорости
осуществляется путём изменения
сопротивлений R1
R2
R3.
Все остальные параметры
схемы
остаются неизменными (Uя,
Iв
и Ф=Фн).
Если считать, что для всех значений
угловой скорости допустимым по
условиям нагрева током является

Рисунок
3.4 - Схема реостатного регулирования
скорости ДПТНВ
его
номинальный ток, т.е. Iя.доп=Iн,
то
допустимый момент при регулировании
скорости равен Мдоп.=кФн·Iя.доп.=
=кФн·Iя.н.=Мн.
Таким
образом, при реостатном регулировании
скорости допустимый момент на
валу двигателя не зависит от скорости
и равен его номинальному моменту.
Иначе говоря, реостатное регулирование
скорости двигателя постоянного тока
независимого возбуждения может быть
осуществлено при постоянном допустимом
моменте статической нагрузки.
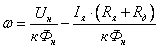 -
уравнение электромеханической
характеристики. -
уравнение электромеханической
характеристики.
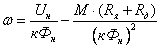 -
уравнение механической характеристики. -
уравнение механической характеристики.
Для
построения характеристик рассмотрим
характерные точки.
Режим
идеального холостого хода:
М=0
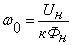
-
т.е скорость идеального холостого
хода не зависит от добавочного
сопротивления в цепи якоря. Все
искусственные механические
характеристики выходят из точки,
соответствующей режиму идеального
холостого хода.
Из
уравнения механической характеристики
следует, что при постоянном моменте
двигателя его угловая скорость
является линейной функцией
сопротивления регулировочного
реостата.
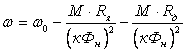 ; ;
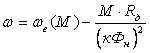 , ,
где
ω0
-
скорость идеального холостого хода;
ωе(М)
-
скорость двигателя, определяемая
по его естественной
характеристике
при заданном значении М.
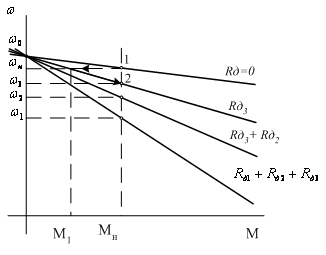
Рисунок
3.5 - Механические характеристики при
реостатном регулировании.
Последний
член в уравнениях представляет собой
падение скорости, обусловленное
введением добавочного сопротивления.
Модуль жёсткости механических
характеристик
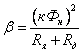 снижается
по мере уменьшения скорости. снижается
по мере уменьшения скорости.
3.5.1.2
Переходный процесс при регулировании
скорости
Рассмотрим
переходный процесс регулирования
скорости.
Пусть Мс=Мн=
const
до и после регулирования,
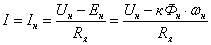 -
до регулирования. -
до регулирования.
При
введении Rд3,
скорость
привода не может измениться мгновенно
в виду механической инерционности,
уменьшается ток якоря → уменьшается
электромагнитный момент двигателя
до значения М1=кФн·I
, но Мс=
const
→
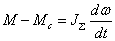 → →
на
валу двигателя появляется отрицательный
динамический момент → торможение
→ скорость уменьшается → уменьшается
э.д.с. двигателя → что приведёт
увеличению тока в якорной цепи и
момента двигателя, при М
= Мс
будет
новый установившийся режим работы
привода с меньшей скоростью ω3
и
Мс
=
Мн
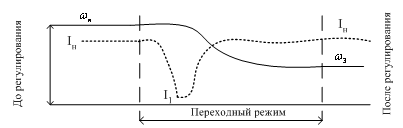
Рисунок
3.6 - Переходный процесс при регулировании
скорости
3.5.1.3
Оценка данного способа регулирования
1.
Из анализа уравнения механической
характеристики следует, что при
изменении Rд
возможно регулирование угловой
скорости только вниз от основной
скорости. В двигательном режиме
все искусственные характеристики
лежат ниже естественной характеристики.
2.
Плавность регулирования скорости
определяется плавностью изменения
добавочного сопротивления. В
большинстве случаев реостатное
регулирование скорости производится
с помощью контакторов, замыкающих
отдельные ступени резисторов, т.е.
скорость привода изменяется
ступенчато.
3.
Главным недостатком реостатного
регулирования является его
энергетическая неэффективность.
Запишем уравнение электрического
равновесия для точки 1и точки 2
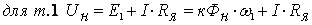
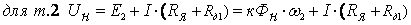
приравняем
левые и правые части
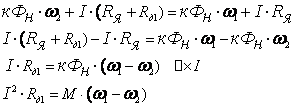
где
(ω1-
ω2)
– диапазон
регулирования скорости;
I2·Rд1
–
потери
мощности в якорной цепи.
Потери
в якорной цепи тем больше, чем шире
диапазон регулирования скорости.
Условие неэкономичности ограничивает
диапазон регулирования скорости. С
увеличением сопротивления в якорной
цепи уменьшается жёсткость
характеристик, а, следовательно,
уменьшается точность регулирования.
Поэтому диапазон не превышает
(1,5÷2):1. Регулирование скорости ведётся
вниз от основной. |
|
3.5.2
Импульсное параметрическое
регулирование скорости
Одним
из способов достижения плавного
регулирования при введении резисторов
в цепь якоря является использование
(при небольшой мощности двигателя)
импульсного параметрического
регулирования угловой скорости,
применяемого также в автоматизированном
электроприводе для стабилизации
(поддержания) заданного значения
угловой скорости при изменении
момента нагрузки или для предварительного
снижения скорости перед остановкой
привода.
Ступенчатое
реостатное регулирование скорости
не всегда удобно, так как при большом
числе ступеней скорости может
потребоваться значительное число
коммутирующих аппаратов, что может
привести к снижению надежности
работы электропривода и связано с
увеличением стоимости электрооборудования.
В связи с этим в последние годы все
более широкое распространение
получают методы импульсного
регулирования отдельных параметров
схемы.
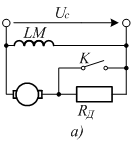 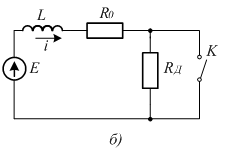
Рисунок
3.7 - Импульсное регулирование скорости
ДПТНВ
В
схеме рис. 3.7, а
в
цепи якоря двигателя постоянного
тока с независимым возбуждением
включено добавочное сопротивление
Rд,
которое либо полностью вводится в
схему, либо замыкается накоротко
ключом К.
Коммутация
ключа К
осуществляется
периодически. При замкнутом накоротко
Rд
ток в цепи якоря возрастает, а при
введении Rд
в цепь, когда ключ К
разомкнут,
ток снижается.
Для
определения количественных
соотношений, характеризующих
работу данной схемы, проанализируем
эквивалентную схему, представленную
на рис 3.7, б,
Здесь
Е
= Uс
-
Е
дв—
суммарная э. д. с. в цепи якоря;
L
—
индуктивность цепи якоря;
Rя
—
нерегулируемая часть сопротивления
цепи якоря.
При
составлении эквивалентной схемы
принято, что скорость двигателя, а
значит, и э. д. с. его якоря Е
дв
за период коммутации ключа К
остаются
неизменными.
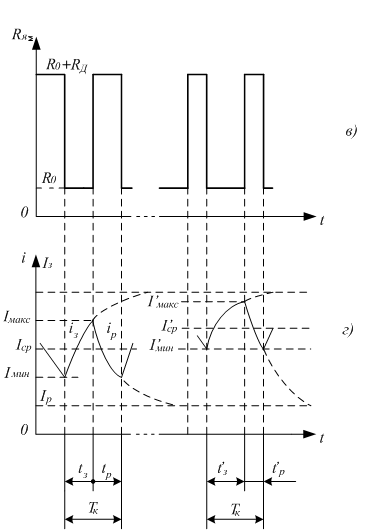
Коммутация
ключа К
обычно
осуществляется таким образом, что
период коммутации Тк
остается
неизменным, а изменяется лишь
соотношение времени замкнутого t3
и
разомкнутого tp
состояний
его контактов. Иными словами,
изменяется ширина замыкающего
импульса. При этом сопротивление в
цепи якоря Rд
изменяется в соответствии с
диаграммой на рис. 3.7, в.
Такой
способ управления величиной
параметра получил название
широтно-импульсного регулирования.
Возможен и другой вариант управления
— частотно-импульсный, когда t3
=
const,
а изменяется период коммутации ключа
Тк,
т.
е. частота коммутации ключа.
Из
теории электрических цепей известно,
что при скачкообразном изменении
Rд,
имеющем место в результате коммутации
К,
в
рассматриваемой эквивалентной схеме
возникает апериодический переходный
процесс. При этом ток в схеме изменяется
по экспоненциальному закону. В период
замыкания К
ток
нарастает по экспоненте с постоянной
времени Тз
= L/Rд,
а
в период размыкания К
ток
спадает по экспоненте с постоянной
времени Тp
=L/(Rя+
Rд).
На
рис. 3.7, г
показано
изменение тока за период коммутации.
При неизменных значениях tз
и
tp
в
схеме имеет место режим работы,
характеризующийся значениями Iмакс
и
Iмин.
Очевидно, что в этом случае будет
также неизменным и среднее значение
тока якоря двигателя.
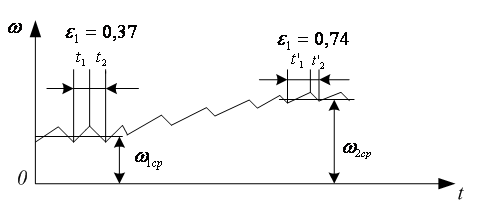
Рисунок
3.8 - График скорости при
импульсном регулировании
Колебания
тока и угловой скорости происходят
около некоторого среднего значения
(рис. 3.8).
Среднее
значение тока определяется моментом
нагрузки на валу двигателя, а среднее
значение угловой скорости зависит
от соотношения длительностей
замкнутого и разомкнутого состояния
ключа К
и
от момента нагрузки. Соотношение
длительностей tз
замкнутого
и tр
разомкнутого
состояний ключа К
принято
выражать в виде относительной
величины ε,
называемой скважностью управляющих
импульсов.
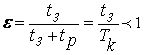 . .
Эквивалентное
(усредненное) добавочное сопротивление
в цепи якоря определяется соотношением
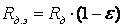 , ,
и
механические характеристики
двигателя, показанные на рис. 3.9,
определяются
формулой (для средних значений
угловой скорости и момента)
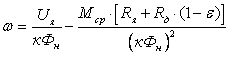 , ,
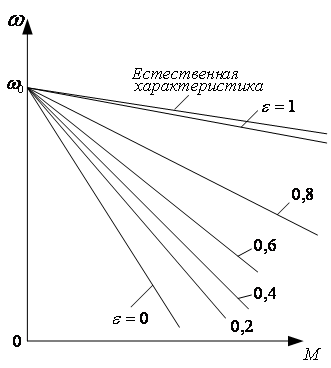
Рисунок
3.9 - Механические характеристики при
импульсном регулировании скорости
ДПТНВ
т.
е. характеристики имеют тот же вид
и те же свойства, что и при реостатном
регулировании угловой скорости.
Очевидно,
что с увеличением ε
при неизменной нагрузке на валу
двигателя угловая скорость его будет
возрастать, а при ε=1 двигатель будет
работать на естественной характеристике
(ключ К
постоянно
замкнут). При ε=0 двигатель будет
работать на реостатной характеристике,
соответствующей постоянно включенному
резистору Яд
(ключ
К
разомкнут).
Для
реализации данного способа
регулирования необходимо создать
ключ, с помощью которого возможно с
относительно большой частотой
замыкать накоротко Яд
или
полностью вводить его в цепь якоря.
Использование для этой цели
механического контактного устройства
практически не представляется
возможным, поскольку оно рассчитано
на ограниченное число циклов
срабатывания и при большой частоте
включений относительно быстро
выходит из строя. Кроме того, время
перемещения контактов при их
замыкании и размыкании относительно
велико, что, с одной стороны,
ограничивает частоту коммутации,
а с другой — ограничивает возможность
точного поддержания заданной величины
относительно времени замыкания
ключа. В связи с этим в технике
регулирования электроприводов
контактные ключи не находят применения.
3.5.3
Регулирование
скорости шунтированием якоря
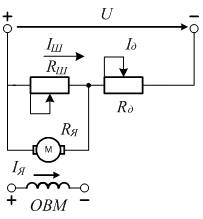
Рисунок
3.10 - Схема шунтирования обмотки
возбуждения ДПТНВ
Для
получения сравнительно жестких
механических характеристик при
малых скоростях применяют иногда
шунтирование якоря резистором Rш
при
обязательном включении
последовательного резистора Rд,
как
это показано на рисунке. Резисторы
Rш
и Rд
представляют
собой
делитель напряжения. Правда, на
работу этого делителя в значительной
степени влияет нагрузка двигателя,
так как потребляемый из сети ток Iд,
а значит, и падение напряжения на
последовательном резисторе Rд
зависят
от тока якоря Iя
двигателя. При таком включении
двигателя используются как бы
одновременно два способа регулирования
угловой скорости двигателя —
изменением подводимого к якорю
напряжения и реостатное, поэтому и
получаемые регулировочные
характеристики двигателя занимают
промежуточное положение между
характеристиками, указанных
способов.
Уравнение
механической характеристики двигателя
в
схеме, представленной на рисунке,
может быть получено
на основании следующих соотношений:
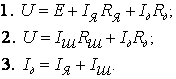
Подставим
3 уравнение во 2 и выразим ток через
шунт:
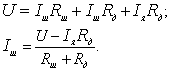
Подставляем
полученное выражение в 1 уравнение:
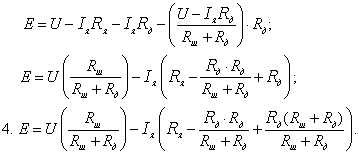
Обозначим
за
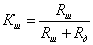
-
коэффициент шунтирования отношение
сопротивлений. Разделим левую и
правую часть уравнения 4 на (кФн)
и подставим величину Кш,
получим уравнение электромеханической
характеристики двигателя при
шунтировании якоря
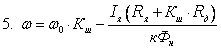 ; ;
Уравнение
механической характеристики имеет
вид:
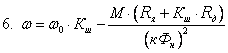 . .
Характеристики
5 и 6 линейны. Кроме того, угловая
скорость идеального холостого хода
двигателя будет меньше, чем при
реостатном регулировании. При М=0,
угловая скорость будет равна Кш·ω0.
Причём
всегда
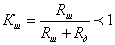 . .
Если
сравнить наклон полученной
характеристики, а также естественной
и реостатной, то можно сделать вывод,
что Δωе<
Δωш<
Δωр.

Рисунок
3.11 - Механические характеристики
ДПТНВ при шунтировании обмотки якоря
На
рисунке 3.11 представлена механическая
характеристика двигателя при
шунтировании якоря, проходящая через
ω0΄.
Там же приведены естественная и
реостатная характеристики
для обычной схемы включения. Из
сопоставления этих
характеристик видны преимущества
рассматриваемой схемы.
Действительно, получение пониженной
угловой скорости ωс΄
возможно
и в обычной схеме путем перехода от
естественной характеристики к
соответствующей реостатной.
Однако из сравнения реостатной
характеристики
с
характеристикой при шунтировании
якоря видно, что последняя,
является значительно более жесткой
и потому обеспечивающей
при возможных отклонениях момента
нагрузки
более стабильное регулирование
угловой скорости.
Жесткость
механической характеристики и
угловая скорость
идеального холостого хода зависят
от соотношения
сопротивлений последовательного и
шунтирующего резисторов.
Если изменить сопротивления этих
резисторов, то
можно получить другой наклон
характеристики.
При
неизменном сопротивлении
последовательного резистора Rд
и
различных значениях
шунтирующего резистора
Rш
и
получаются семейства характеристик.
Предположим,
что изменяется сопротивление шунта
от Rш=0
до
Rш=∞.
Постоим
характеристику при Rш=∞
(обрыв
цепи Rш)
→
Iш=0
→ Iя=Iд
- двигатель
работает на реостатной характеристике
с включённым Rд
Построим
характеристику при
Rш=0:
Кш=0
Уравнение
характеристики
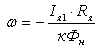 . .
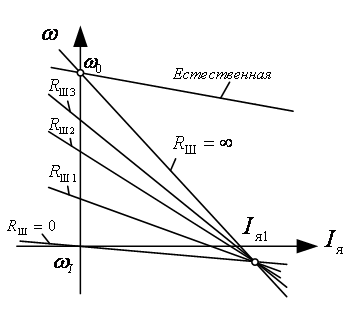
а)

Рисунок
3.12 - Электромеханические характеристики
а)
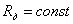 и и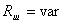 ;
б) ;
б)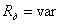 и и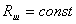 . .
Первая
точка характеристики
Iя=0
→ ω=0
Найдём
вторую точку – точку пересечения
характеристик при
Rш=0
и
Rш=∞
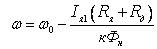 и и
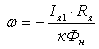 ; ;
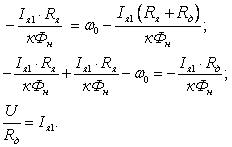

Характеристики
показаны на рисунке 3.12 а.
При
неизменном сопротивлении шунтирующего
резистора Rш
и различных значениях сопротивлениях
добавочного сопротивления от Rд
=0 до
Rд=∞
построим семейство характеристик.
Если
Rд=0,
то
характеристика будет естественной,
т.к
Кш=1
и
уравнения 5 и 6 принимают вид
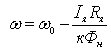 . .
Точку
пересечения характеристик найдём
совместным решением уравнений
естественной и искусственной (с
добавочным сопротивлением Rд1)
характеристик
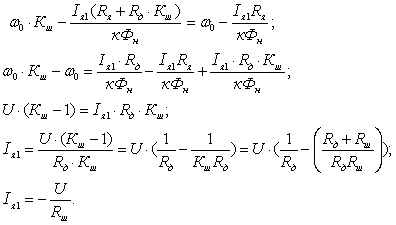
Поставим
значение тока в уравнение скоростной
характеристики и получим значение
скорости для этого режима
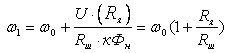 . .
Если
Rд=∞,
Кш=0.
Это
соответствует режиму, когда
сопротивление последовательного
резистора не будет влиять на ток
якоря, т.е. ток через последовательный
резистор проходить не будет.
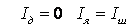 это
означает, что двигатель из сети
питания не получает и работает
генератором на Rш,
уравнение
характеристики имеет вид это
означает, что двигатель из сети
питания не получает и работает
генератором на Rш,
уравнение
характеристики имеет вид
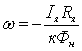 . .
Вторая
точка предельной характеристики:
Iя=0
→ ω=0.
Характеристики показаны на рисунке
3.12 б.
Выводы:
1.Обладает
теми же показателями, что и реостатное
регулирование.
2.
Использование для регулирования
напряжения сопротивлений является
простым и дешёвым техническим
решением, однако потери энергии в
сопротивлениях Rш
и
Rд
больше, чем при реостатном регулировании.
Эти потери возрастают с уменьшением
внутреннего сопротивления потенциометра
и соответствующим увеличением
получаемой жёсткости характеристики.
3.
Схема с шунтированием якоря
используется в приводах небольшой
мощности, для предварительного
снижения скорости перед точной
остановкой механизма. 3.6
Регулирование угловой скорости
двигателя постоянного тока независимого
возбуждения изменением магнитного
потока
Регулирование
угловой скорости двигателя изменением
тока
возбуждения является одним из
наиболее простых и
экономичных способов. Мощность,
потребляемая обмоткой
возбуждения двигателя, составляет
примерно 2—2,5 % мощности
двигателя, поэтому этот способ
находит широкое
применение в современной практике
электропривода.
Принципиальные
схемы электропривода при регулировании
тока возбуждения показаны на рис.
3.13, а,
б. Ток
возбуждения
регулируется или с помощью резистора,
(рис 3.13, а)
в
случае двигателей малой мощности,
или посредством регулятора напряжения
РН
(рис.
3.13, б).
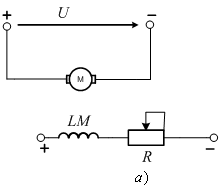 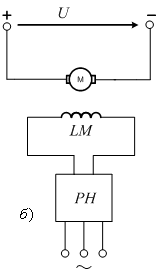
Рисунок
3.13 - Схема электропривода при
регулировании тока возбуждения
Электромеханическим
характеристикам ω=f(I)
при изменении тока возбуждения
соответствуют различные значения
угловой скорости идеального холостого
хода из уравнения скоростной
характеристики
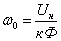 . .
На
рисунке по оси ординат отложено
значение угловой скорости идеального
холостого хода ω0
для естественной характеристики,
когда поток Ф = Фном.
Значения угловых скоростей идеального
холостого хода при ослабленном
потоке ω0΄
и
ω0΄΄
лежат,
очевидно, выше ω0.
Все электромеханические характеристики
пересекаются с осью абсцисс в одной
точке. Последнее следует из того,
что при ω = 0 уравнение для любой
электромеханической характеристики
имеет вид:
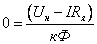 ,
откуда определяется ток в якоре
двигателя ,
откуда определяется ток в якоре
двигателя
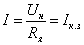 . .
Следовательно,
при различных токах возбуждения и
при угловой скорости двигателя,
равной нулю, ток в якорной цепи
равен току короткого замыкания
двигателя. Этим значением тока и
определяется общая точка пересечения
электромеханических характеристик.
Механические
характеристики, показанные на
рисунке, имеют те же значения угловых
скоростей идеального холостого
хода, что и для электромеханических
характеристик.
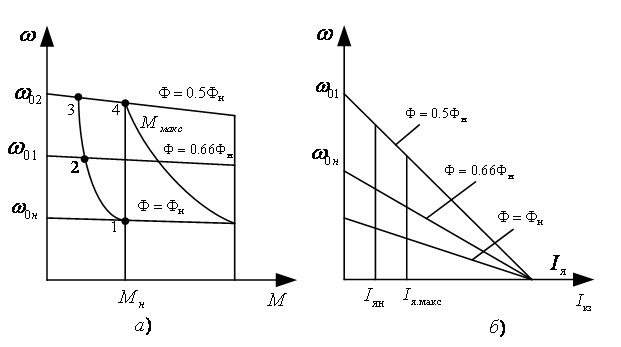
Рисунок
3.14 - Механические (а) и электромеханические
(б) характеристики двигателя
постоянного тока независимого
возбуждения при уменьшении потока
возбуждения и номинальном напряжении
якоря
Однако
эти характеристики не пересекаются
в одной точке на оси абсцисс, так как
по мере, уменьшения потока уменьшается
и момент короткого замыкания,
определяемый по формуле
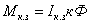
Полному
использованию двигателя соответствуют
точки, находящиеся на линии номинального
тока I
=Iном
этому
соответствуют точки, лежащие на
гиперболической кривой момента
сопротивления МС
как это показано пунктиром на
механических характеристиках.
При
анализе механических характеристик
при ослаблении поля следует иметь
в виду, что при работе с постоянным
статическим моментом ток якоря
по мере ослабления потока увеличивается.
Так, если статический момент на валу
двигателя будет равен номинальному,
то при номинальном напряжении якоря
Uян
двигатель
будет работать в т.1 (см. рис.3.14,а).
Если, например, ослабить поток
возбуждения в 2 раза, то скорость
холостого хода двигателя ω02
увеличивается в 2 раза. Если момент
двигателя сохранится постоянным
и равным номинальному, то двигатель
будет работать в т.4.
Однако,
как это следует из
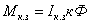 ток
якоря при этом увеличится в 2 раза.
Поэтому длительная работа двигателя
в т.4 недопустима. Из этого примера
следует, что одновременно с повышением
скорости необходимо снижать
длительно допустимый по условия
нагрева (номинальный) момент. Линия
номинального момента при ослаблении
поля отображается кривой 1-2-3.
Аналогично
при ослаблении поля уменьшается
допустимый максимальный момент.
Поскольку при ослаблении поля
скорость увеличивается примерно
пропорционально степени ослабления
поля Фн/Фосл,
а
длительно допустимый момент Мдоп
уменьшается
пропорционально отношению Фосл
/Фн,
то
длительно допустимая мощность
двигателя Р
= М·ω остается
примерно постоянной. Поэтому
регулирование ослаблением поля
называют регулированием с постоянной
мощностью в отличие от регулирования
изменением напряжения якоря при
постоянном потоке возбуждения,
которое называют регулированием с
постоянным моментом. ток
якоря при этом увеличится в 2 раза.
Поэтому длительная работа двигателя
в т.4 недопустима. Из этого примера
следует, что одновременно с повышением
скорости необходимо снижать
длительно допустимый по условия
нагрева (номинальный) момент. Линия
номинального момента при ослаблении
поля отображается кривой 1-2-3.
Аналогично
при ослаблении поля уменьшается
допустимый максимальный момент.
Поскольку при ослаблении поля
скорость увеличивается примерно
пропорционально степени ослабления
поля Фн/Фосл,
а
длительно допустимый момент Мдоп
уменьшается
пропорционально отношению Фосл
/Фн,
то
длительно допустимая мощность
двигателя Р
= М·ω остается
примерно постоянной. Поэтому
регулирование ослаблением поля
называют регулированием с постоянной
мощностью в отличие от регулирования
изменением напряжения якоря при
постоянном потоке возбуждения,
которое называют регулированием с
постоянным моментом.
Особенности
регулирования:
Обычно
регулируемые двигатели имеют диапазон
регулирования от 2:1 до 5:1, в ряде
случаев до (8-10) : 1.
Диапазон
регулирования ограничивается
различными факторами. Главным из
них является ухудшение условий
коммутации с возрастанием угловой
скорости, поскольку реактивная ЭДС,
вызывающая искрение на коллекторе,
пропорциональна току и угловой
скорости, т. е. Ер
= сIω.
Кроме того, при больших угловых
скоростях требуется повышать
механическую прочность якоря. Нижний
предел угловой скорости ограничивается
степенью насыщения машины и нагревом
обмотки возбуждения; т. е. номинальной
угловой скоростью.
Плавность
регулирования в пределах заданного
диапазона может быть получена
весьма значительной и определяется
количеством ступеней регулировочного
реостата или же числом ступеней
специальных устройств, регулирующих
напряжение, подводимое к обмотке
возбуждения.
Стабильность
угловой скорости при регулировании
определяется относительным перепадом
угловой скорости при изменении
нагрузки и в данном случае при
номинальном токе якоря как,
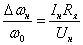 , ,
поэтому
независимо от тока возбуждения
относительный перепад сохраняется
одним и тем же для естественной и
искусственной характеристик, т. е.
угловая скорость сравнительно
стабильна.
Для
электроприводов многих механизмов
используют комбинированное
управление, так называемое двухзонное
регулирование скорости. В первой
зоне скорость двигателя в диапазоне
от нуля до основной скорости ωн
регулируется
изменением напряжения якоря при
постоянном потоке возбуждения
Фн.
Во
второй зоне регулирование производится
изменением тока (потока) возбуждения
при постоянном номинальном напряжении
якоря. Соответственно номинальный
момент в первой зоне регулирования
остается постоянным, а во второй
зоне снижается пропорционально
уменьшению потока. Максимально
допустимая скорость двигателя
при ослаблении поля определяется
механической прочностью якоря и
условиями коммутации на коллекторе.
Эта скорость указывается в каталоге
на двигатели.
Ослабление
поля используется и при однозонном
регулировании скорости для
установления основной (максимальной)
скорости. В отличие от синхронных
и асинхронных двигатели постоянного
тока не имеют жестко определенной
номинальной скорости. В каталогах
указывается номинальная и максимальная
скорости. Например, если указано,
что двигатель мощностью 100кВт имеет
номинальную скорость 1000 об/мин и
максимальную – 2000 об/мин, то
основная скорость может быть
установлена в этих пределах выбором
соответствующего значения тока
возбуждения, например, - 1600 об/мин.
При этом мощность двигателя
останется равной 100кВт. Это удобно
при конструировании кинематической
схемы рабочей машины 3.7
Регулирование угловой скорости ДПТ
НВ изменением подводимого к якорю
напряжения
Регулирование
угловой скорости двигателя изменением
тока
возбуждения является одним из
наиболее простых и
экономичных способов. Мощность,
потребляемая обмоткой
возбуждения двигателя, составляет
примерно 2—2,5 % мощности
двигателя, поэтому этот способ
находит широкое
применение в современной практике
электропривода.
Принципиальные
схемы электропривода при регулировании
тока возбуждения показаны на рис.
3.13, а,
б. Ток
возбуждения
регулируется или с помощью резистора,
(рис 3.13, а)
в
случае двигателей малой мощности,
или посредством регулятора напряжения
РН
(рис.
3.13, б).
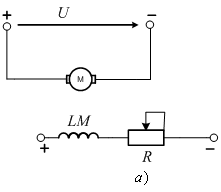 
Рисунок
3.13 - Схема электропривода при
регулировании тока возбуждения
Электромеханическим
характеристикам ω=f(I)
при изменении тока возбуждения
соответствуют различные значения
угловой скорости идеального холостого
хода из уравнения скоростной
характеристики
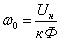 . .
На
рисунке по оси ординат отложено
значение угловой скорости идеального
холостого хода ω0
для естественной характеристики,
когда поток Ф = Фном.
Значения угловых скоростей идеального
холостого хода при ослабленном
потоке ω0΄
и
ω0΄΄
лежат,
очевидно, выше ω0.
Все электромеханические характеристики
пересекаются с осью абсцисс в одной
точке. Последнее следует из того,
что при ω = 0 уравнение для любой
электромеханической характеристики
имеет вид:
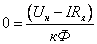 ,
откуда определяется ток в якоре
двигателя ,
откуда определяется ток в якоре
двигателя
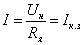 . .
Следовательно,
при различных токах возбуждения и
при угловой скорости двигателя,
равной нулю, ток в якорной цепи
равен току короткого замыкания
двигателя. Этим значением тока и
определяется общая точка пересечения
электромеханических характеристик.
Механические
характеристики, показанные на
рисунке, имеют те же значения угловых
скоростей идеального холостого
хода, что и для электромеханических
характеристик.

Рисунок
3.14 - Механические (а) и электромеханические
(б) характеристики двигателя
постоянного тока независимого
возбуждения при уменьшении потока
возбуждения и номинальном напряжении
якоря
Однако
эти характеристики не пересекаются
в одной точке на оси абсцисс, так как
по мере, уменьшения потока уменьшается
и момент короткого замыкания,
определяемый по формуле
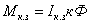
Полному
использованию двигателя соответствуют
точки, находящиеся на линии номинального
тока I
=Iном
этому
соответствуют точки, лежащие на
гиперболической кривой момента
сопротивления МС
как это показано пунктиром на
механических характеристиках.
При
анализе механических характеристик
при ослаблении поля следует иметь
в виду, что при работе с постоянным
статическим моментом ток якоря
по мере ослабления потока увеличивается.
Так, если статический момент на валу
двигателя будет равен номинальному,
то при номинальном напряжении якоря
Uян
двигатель
будет работать в т.1 (см. рис.3.14,а).
Если, например, ослабить поток
возбуждения в 2 раза, то скорость
холостого хода двигателя ω02
увеличивается в 2 раза. Если момент
двигателя сохранится постоянным
и равным номинальному, то двигатель
будет работать в т.4.
Однако,
как это следует из
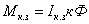 ток
якоря при этом увеличится в 2 раза.
Поэтому длительная работа двигателя
в т.4 недопустима. Из этого примера
следует, что одновременно с повышением
скорости необходимо снижать
длительно допустимый по условия
нагрева (номинальный) момент. Линия
номинального момента при ослаблении
поля отображается кривой 1-2-3.
Аналогично
при ослаблении поля уменьшается
допустимый максимальный момент.
Поскольку при ослаблении поля
скорость увеличивается примерно
пропорционально степени ослабления
поля Фн/Фосл,
а
длительно допустимый момент Мдоп
уменьшается
пропорционально отношению Фосл
/Фн,
то
длительно допустимая мощность
двигателя Р
= М·ω остается
примерно постоянной. Поэтому
регулирование ослаблением поля
называют регулированием с постоянной
мощностью в отличие от регулирования
изменением напряжения якоря при
постоянном потоке возбуждения,
которое называют регулированием с
постоянным моментом. ток
якоря при этом увеличится в 2 раза.
Поэтому длительная работа двигателя
в т.4 недопустима. Из этого примера
следует, что одновременно с повышением
скорости необходимо снижать
длительно допустимый по условия
нагрева (номинальный) момент. Линия
номинального момента при ослаблении
поля отображается кривой 1-2-3.
Аналогично
при ослаблении поля уменьшается
допустимый максимальный момент.
Поскольку при ослаблении поля
скорость увеличивается примерно
пропорционально степени ослабления
поля Фн/Фосл,
а
длительно допустимый момент Мдоп
уменьшается
пропорционально отношению Фосл
/Фн,
то
длительно допустимая мощность
двигателя Р
= М·ω остается
примерно постоянной. Поэтому
регулирование ослаблением поля
называют регулированием с постоянной
мощностью в отличие от регулирования
изменением напряжения якоря при
постоянном потоке возбуждения,
которое называют регулированием с
постоянным моментом.
Особенности
регулирования:
Обычно
регулируемые двигатели имеют диапазон
регулирования от 2:1 до 5:1, в ряде
случаев до (8-10) : 1.
Диапазон
регулирования ограничивается
различными факторами. Главным из
них является ухудшение условий
коммутации с возрастанием угловой
скорости, поскольку реактивная ЭДС,
вызывающая искрение на коллекторе,
пропорциональна току и угловой
скорости, т. е. Ер
= сIω.
Кроме того, при больших угловых
скоростях требуется повышать
механическую прочность якоря. Нижний
предел угловой скорости ограничивается
степенью насыщения машины и нагревом
обмотки возбуждения; т. е. номинальной
угловой скоростью.
Плавность
регулирования в пределах заданного
диапазона может быть получена
весьма значительной и определяется
количеством ступеней регулировочного
реостата или же числом ступеней
специальных устройств, регулирующих
напряжение, подводимое к обмотке
возбуждения.
Стабильность
угловой скорости при регулировании
определяется относительным перепадом
угловой скорости при изменении
нагрузки и в данном случае при
номинальном токе якоря как,
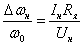 , ,
поэтому
независимо от тока возбуждения
относительный перепад сохраняется
одним и тем же для естественной и
искусственной характеристик, т. е.
угловая скорость сравнительно
стабильна.
Для
электроприводов многих механизмов
используют комбинированное
управление, так называемое двухзонное
регулирование скорости. В первой
зоне скорость двигателя в диапазоне
от нуля до основной скорости ωн
регулируется
изменением напряжения якоря при
постоянном потоке возбуждения
Фн.
Во
второй зоне регулирование производится
изменением тока (потока) возбуждения
при постоянном номинальном напряжении
якоря. Соответственно номинальный
момент в первой зоне регулирования
остается постоянным, а во второй
зоне снижается пропорционально
уменьшению потока. Максимально
допустимая скорость двигателя
при ослаблении поля определяется
механической прочностью якоря и
условиями коммутации на коллекторе.
Эта скорость указывается в каталоге
на двигатели.
Ослабление
поля используется и при однозонном
регулировании скорости для
установления основной (максимальной)
скорости. В отличие от синхронных
и асинхронных двигатели постоянного
тока не имеют жестко определенной
номинальной скорости. В каталогах
указывается номинальная и максимальная
скорости. Например, если указано,
что двигатель мощностью 100кВт имеет
номинальную скорость 1000 об/мин и
максимальную – 2000 об/мин, то
основная скорость может быть
установлена в этих пределах выбором
соответствующего значения тока
возбуждения, например, - 1600 об/мин.
При этом мощность двигателя
останется равной 100кВт. Это удобно
при конструировании кинематической
схемы рабочей машины.
3.7.1
Система генератор – двигатель (Г-Д)
Данная
система считается, в настоящее время
морально устаревшей. Но по оценкам
зарубежных специалистов этот привод
ещё будут долго использовать при
больших мощностях (сотни кВт) и
двунаправленных потоках энергии, а
также при желании избежать проблем
с электромагнитной совместимостью.
Представляется, что именно, эта
система, а не система ТП-Д продлит
жизнь мощных приводов постоянного
тока.
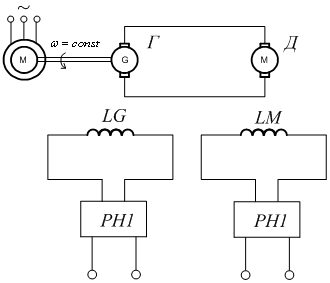
Рисунок
3.16 - Система генератор-двигатель
Якорь
двигателя М
присоединяется
к якорю генератора G
непосредственно.
Электродвижущая сила генератора
определяется по формуле
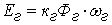 . .
где
kг
—
коэффициент, зависящий от конструктивных
данных генератора и определяемый
по формуле
kг
= pгNг/2πaг,
следовательно,
при постоянной угловой скорости
генератора ωг
ЭДС его будет определяться магнитным
потоком, который легко регулируется
током возбуждения.
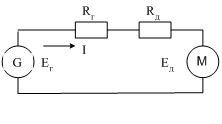
Рисунок
3.17 - Схема замещения системы Г-Д
Пользуясь
схемой замещения для рассматриваемого
случая (рис3.17), можно составить
уравнение равновесия ЭДС
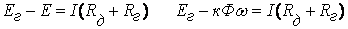 , ,
где
Е и I
– э.д.с. двигателя и ток якорной цепи
машины,
Rг
,Rд
– соответственно сопротивление
якоря генератора и двигателя.
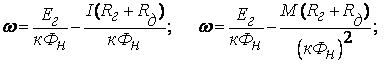
т.к.
М=кФн·I,
то при неизменном потоке двигателя
ω=ω0
-В·М,
где

Механические
характеристики при неизменном потоке
двигателя и изменении потока
генератора представляют собой
семейство линейных характеристик,
наклон которых остается постоянным
и определяется общим сопротивлением
якорной цепи. Скорость идеального
холостого хода определяется по
формуле
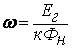
и
может приобретать любое значение
от
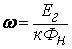 до до . .
Отрицательное
значение ЭДС генератора можно
получить при реверсировании тока
возбуждения изменением полярности
напряжения на обмотке возбуждения
генератора. Механические характеристики
располагаются в четырёх квадрантах,
основным достоинством этой системы
является плавность регулирования,
которая осуществляется воздействием
на цепь возбуждения.
Система
Г-Д может обеспечить и двухзонное
регулирование угловой скорости.
Верхний предел угловой скорости при
регулировании с постоянным потоком
двигателя ограничивается
номинальным значением э.д.с. генератора
и перепадом скорости, который
обусловлен нагрузкой и сопротивлением
якорной цепи. Нижний предел
регулирования ограничивается
заданным относительным перепадом
угловой скорости при заданном
изменении нагрузки, этот относительный
перепад, нгазывается статизмом,
определяется при минимальной угловой
скорости для случая изменения
нагрузки от нуля до номинального
как
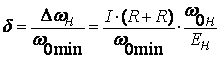 . .
Отсюда
допустимый диапазон регулирования
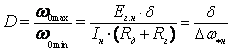 . .
Если,
например, принять относительный
перепад скорости Δω*н=0,1,
то при допустимом статизме δ=0,2
допустимый диапазон регулирования
составит D=2:1,
если задаться меньшим статизмом
δ<0,1, то осуществлять регулирование
нельзя, т.к. D<1.
К
недостаткам системы Г-Д относятся:
1)
необходимость в двукратном
преобразовании энергии (из электрической
энергии переменного тока в механическую
и из механической вновь в электрическую
постоянного тока регулируемого
напряжения), что приводит к значительному
снижению КПД;
2)
наличие двух машин в преобразовательном
агрегате, установленная мощность
каждой, если пренебречь потерями
в машинах, равна установленной
мощности регулируемого двигателя;
3)
значительные габариты и масса
установки, необходимость в
фундаменте для преобразовательного
агрегата;
4)
высокие капитальные и
эксплуатационные расходы.
3.7.2
Система тиристорный преобразователь
– двигатель (ТП-Д)
Система
ТП-Д является основной системой
регулируемого электропривода
постоянного тока. Тиристорный
преобразователь в схемах ЭП выполняет
две функции: выпрямление переменного
напряжения и регулирование средней
величины выпрямленного напряжения.
Основу
схем с ТП составляют полупроводниковые
приборы – тиристоры. Неполная
управляемость тиристоров определяется
тем, что включение тиристора
контролируется системой управления
(СИФУ) – при подаче отпирающего
импульса на управляющий электрод
он открывается и остаётся включённым
после снятия отпирающего импульса.
Закрывается тиристор после изменения
полярности напряжения анод-катод и
спадания тока до нуля.
Существуют
запираемые тиристоры GTO,
которые допускают запирание по цепи
управления. Отрицательный импульс
на управляющем электроде выключает
тиристор.
Рассмотрим
на примере однофазной нулевой 2-х
полупериодной схеме выпрямления.
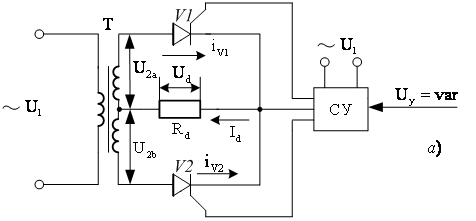
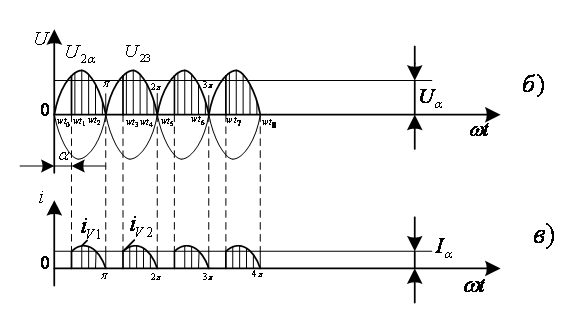
Рисунок
3.18 - Система тиристорный
преобразователь-двигатель
Допустим,
что на управляющий электрод тиристора
V1
подается
от системы управления СУ
отрицательный
импульс в момент времени t1.
Угол
α, отсчитываемый от момента
естественного включения вентиля
V1,
вызовет
на нагрузке скачок напряжения,
которое будет изменяться по кривой
u2a.
В
момент t2
напряжение
u2a
становится
равным нулю и тиристор V1
закрывается.
На интервале t2
— t3
оба тиристора закрыты и ток равен
нулю, а в момент t3
вступает
в действие тиристор V2
и
остается открытым до момента t4
и т. д.
Если
отпирающие импульсы на тиристоры
будут подаваться с запаздыванием
относительно момента естественного
открывания тиристоров на угол α, то
среднее выпрямленное напряжение
преобразователя будет уменьшаться.
При
активной нагрузке кривая выпрямленного
тока повторяет кривую выпрямленного
напряжения, ток имеет прерывистый
характер.
Среднее
значение выпрямленного напряжения
соответствует заштрихованной площади
фигуры.
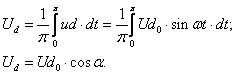
Ud0
– максимальное напряжение
преобразователя на холостом ходу и
полностью открытых тиристорах.
Ud0
= Kcx·Uл.
Уравнение
механической характеристики
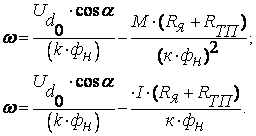
где
RТП
=
RТ
+
RL
+ RК.
Преобразователь
может работать в выпрямительном и
в инверторном режимах. α
= 0 ÷ π/2, Ud
›
Eя
Знак Id
совпадает со знаком выпрямителя Ud.
Инверторный режим имеет место в
реверсивных схемах и получается при
α = π/2 ÷11π/12, Eя
› Ud.. 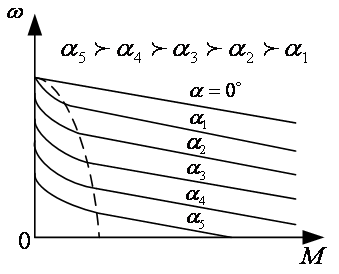
Рисунок
3.19 - Механические характеристики
системы ТП-Д
Преобразователь
подсоединяется к питающей сети или
через трансформатор, служащий, для
согласования напряжения питающей
сети и двигателя, или через сетевой
реактор (токоограничивающий реактор).
Выпрямленный ток имеет непрерывный
характер, если индуктивность в цепи
выпрямленного тока достаточно
велика. Если ток якоря принимает
прерывистый характер, тогда
механические характеристики привода
становятся нелинейными. При желании
уменьшить зону прерывистых токов
последовательно с якорем включают
сглаживающий дроссель, одновременно
сглаживаются пульсации выпрямленного
тока. Механические характеристики
нереверсивного привода ТП-Д не
пересекают ось ординат, т.к изменение
направления тока невозможно,
следовательно, невозможен режим
рекуперативного торможения. В случае
необходимости изменения направления
вращения приводного двигателя в
нереверсивных приводах изменяют
направление тока в обмотке возбуждения.
Для
работы во всех четырёх квадрантах,
необходимо использовать две группы
тиристоров, включённых по
встречно-параллельной схеме. 3.7.3
Система широтно-импульсный
преподаватель – двигатель (ШИП –
ДПТ)
Регулирование
напряжения на якоре движения можно
осуществлять импульсным методом,
когда двигатель периодически
подключается к источнику питания и
отключается от него. В период
отключения ЭП продолжает работать
за счёт запасной энергии кинетической
и электромагнитной.
Основу
данной системы составляют силовые
транзисторные ключи IGBT
(биполярные транзисторы с изолированным
затвором). С управляемым напряжением
затвора. Частота переключений 2 ÷
20кГц, Напряжение до U=1,5
кВ. Ток
до 1кА. Идеальный прибор коммутации
силовых целей. 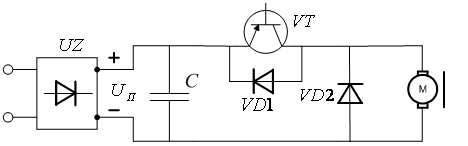
Рисунок
3.20 - Система ШИП-ДПТ
В
этой схеме якорная цепь двигателя
периодически подключается к
источнику питания постоянного тока
(неуправляемый выпрямитель UZ),
имеющему постоянную величину
напряжения Un.
Включение
- отключение напряжения питания
осуществляется ключом - транзистором
VT.
Частота коммутаций цепи постоянная,
равная fk=1/Тк.
Величина
среднего напряжения Ucp
определяется отношением времени
включённого состояния ключа tв
ко времени периода коммутации γ =
tв/Tк
– скважность импульсов γ = 0- 0.95.
При
размыкании ключа ток в якорной цепи
прекратиться мгновенно не может,
т.к. цепь якоря обладает индуктивностью.
VD2
– диод шунтирующий якорь двигателя
создает цепь для протекания тока
якоря под действием ЭДС самоиндукции
в момент разомкнутого состояния
ключа VT.
Это создаёт условия для непрерывного
протекания тока якоря. Величина
пульсаций тока зависти от частоты
коммутации, чем выше частота, тем
меньше амплитуда пульсаций. 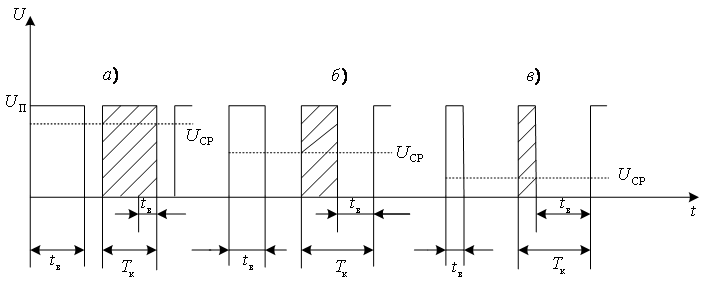
Рисунок
3.21 - Диаграмма напряжений системы
ШИП-ДПТ
Если
время включённого состояния велико
tв
= 0,95 Тк,
то
среднее напряжение поступающее на
двигатель будет максимальным.
Umax
=
0,95·UП.
Если
уменьшить время включённого состояния
ключа VT,
то среднее значение напряжения Uср,
будет уменьшаться (оно пропорционально
заштрихованной площади). Среднее
напряжение поступающее в якорную
цепь равно
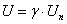 UП
– зависит от схемы выпрямления. При
достаточно мощном фильтровом
конденсаторе С она приближается к
амплитудному значению линейного
напряжения. Уравнения характеристик
привода при ШИП UП
– зависит от схемы выпрямления. При
достаточно мощном фильтровом
конденсаторе С она приближается к
амплитудному значению линейного
напряжения. Уравнения характеристик
привода при ШИП
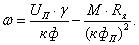
3.7.3.2
Реверсивная система ШИП-ДПТ
Для
реализации реверсивного привода с
ШИП используется мостовая схема
включения силовых транзисторных
ключей. Якорь включён в диагональ
моста ключей VT1
÷ VT4.
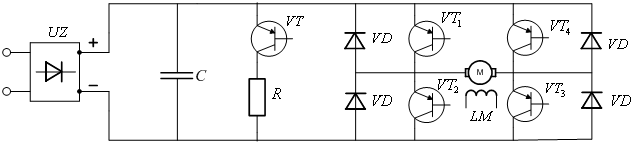
Рисунок
3.22 - Реверсивная система ШИП-Д
Наиболее
простым способом управления ШИП по
цепи якоря является симметричный
(двуполярная коммутация). При
симметричном способе управления в
состоянии переключения находятся
все четыре транзисторные ключа
моста, а напряжение на выходе ШИП
представляет собой знакопеременные
импульсы (изменяется полярность
источника питания в цепи нагрузки),
длительность которых регулируется
входным сигналом.
Протекание
тока в одном направлении происходит
через ключи VT1
– VT3,
а в другом через VT2
– VT4.
Для обеспечения непрерывности служат
обратные диоды. В течении tв
включены
ключи - VT1
– VT4,
а в течение Тк
-
tв
включены
ключи VT2
– VT4.
Ucp
будет пропорционально разности
заштрихованных площадей: tв
>0,5 Тк
Ucp
– положительно, когда tв
= 0,5 Тк Uср=
0, tв
<
0,5 Тк
Ucp
– отрицательно. Величина
среднего выпрямленного напряжения
Ucp
= UП
(2γ – 1); где
γ = tв
/
Tk
- отношение времени включённого
состояния ключей TV1
– TV3
ко времени периода. Симметричный
способ управления используется в
маломощных приводах постоянного
тока. Его преимуществом является
простота реализации И отсутствие
зоны прерывистых токов. Недостатком
ШИП с симметричным способом управления
является знакопеременное напряжение
на нагрузке и в связи с этим повышенные
пульсации тока якорной цепи. 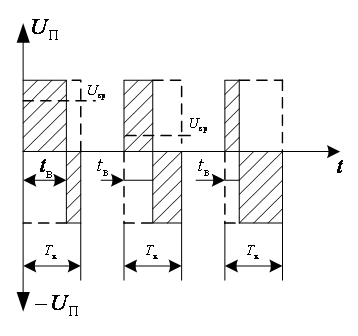
Рисунок
3.23 - Диаграмма напряжений для
реверсивной системы ШИП-ДПТ
Устранение
этого недостатка обеспечивает
однополярное управление (несимметричное
и поочерёдное). В этом случае
переключаются ключи фазной группы
VT3-VT4
(ключи VT1-VT2
при противоположной полярности),
ключ VТ1-всегда
открыт, а ключ VТ2
–постоянно закрыт. Транзисторные
ключи VT3-VT4
переключаются в противофазе,
обеспечивая протекание тока от
противо эдс двигателя. При этом на
ШИП формируются знакопостоянные
импульсы и среднее напряжение
определяется выражением
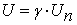 . .
Процесс
торможения в реверсивном электроприводе
постоянного тока с ШИР происходит
следующим образом. Если в
двигательном режиме для выбранного
направления вращения работали
транзисторные ключи VT1
и VT3,
то в режиме торможения эти ключи
будут закрыты и открываются ключи
VT4
и
VT2,
которые также работают в
широтно-импульсном режиме. Ток в
цепи якоря двигателя меняет свое
направление, совпадая по направлению
с э.д.с. якоря Ея.
Величина тока ограничивается на
требуемом уровне посредством
широтно-импульсного регулирования
работы ключей VT4
и VT2.
Ток якоря попеременно проходит
через эти ключи, когда они открыты,
и через обратные диоды VD,
включенные встречно параллельно
ключам VT1
и VT3
(когда ключи VT4
и VT2
закрыты). В первом случае энергия
торможения накапливается в
индуктивности обмоток якоря. Во
втором случае энергия торможения
расходуется на подзаряд конденсатора
С, напряжение на котором под действием
суммы э.д.с. якоря и э.д.с. самоиндукции
обмоток якоря растет. Благодаря
этому источник питания UZ
в самом начале процесса торможения
оказывается заперт. Когда напряжение
на конденсаторе достигнет определенной
величины, открывается транзистор
VT5
и происходит частичный разряд
конденсатора на тормозное сопротивление
R.
В
схемах с широтно-импульсными
регуляторами и нерегулируемым
источником постоянного тока режим
торможения с отдачей энергии в
сеть невозможен. 3.8
Система источник тока – двигатель
(ИТ-Д)
3.8.1
Механические характеристики системы
ИТ-Д
Регулирование
момента двигателя постоянного
тока с независимым возбуждением
обеспечивается при питании якорной
цепи от источника тока. Схема
электропривода по системе источник
тока — двигатель (ИТ — Д) представлена
на рисунке. Здесь якорь двигателя
обтекается неизменным
током Iя
= const,
а
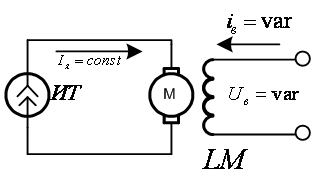
Рисунок
3.24 - Общий вид системы ИТ-Д
управление
электроприводом осуществляется
воздействием на цепь возбуждения
путем изменения подводимого
напряжения uв
= var
и соответственно тока возбуждения
Iв
= var.
При
неизменном токе якоря момент двигателя
пропорционален потоку: М
=
кIномФ
= kмФ.
поэтому, изменяя поток двигателя,
можно регулировать момент, как по
значению, так и по знаку.
Питание
двигателя от источника тока полностью
исключает электромеханическую
связь, так как любые изменения
скорости и соответственно ЭДС
двигателя компенсируются без
запаздывания изменением ЭДС источника
питания. Напомним, что раньше эта
ЭДС играла исключительно важную
роль, определяя вместе с Еп
ток,
а следовательно, и момент машины и
вместе с Мс
- ее
скорость. Теперь Е=кФω
играет
вспомогательную роль и определяет
лишь напряжение на выводах машины
U=
E
+ IR
(в
R
кроме
Rя
может
входить и сопротивление дополнительно
включенного резистора Rд).
При
малых Rя
и Rд=0
иногда можно не считаться с членом
IR
и
полагать U
≈Е.
При
этом ток нагрузки поддерживается
неизменным. При Ф = const
двигатель развивает постоянный
момент при любых возмущениях, в том
числе и при реальных пределах
изменения скорости.
Естественные
характеристики определяются, не
только параметрами машины, но и типом
преобразователя. Будем называть
естественными характеристиками в
приводе источник тока — двигатель
зависимости
I
ном
= const;
Мном
= const
и U
=
kФномω
+ Iном
Rя.
Механические
характеристики для различных значений
потока двигателя в пределах от —
Фном
до +Фном
показаны на рис. Рассматривая их,
можно установить, что электропривод
по системе ИТ - Д обладает свойствами
полностью управляемого источника
момента, обеспечивающего при Ф=var
точное и плавное регулирование
момента в пределах от — Мном
до +Мном
как в двигательном, так и в тормозном
режимах при любом направлении
скорости.
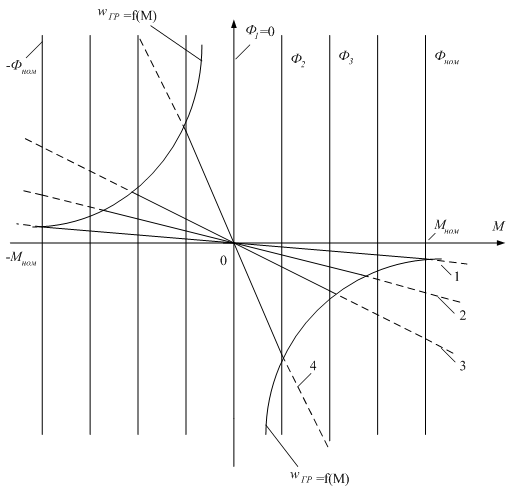
Рисунок
3.25 - Механические характеристики
системы ИТ-Д
Заметим,
что для получения знакопеременного
момента в данном случае не требуется
изменения направления тока якоря,
поэтому источник тока может обладать
односторонней проводимостью. Эти
условия определяют минимальные
габариты преобразователя, на базе
которого может быть реализован
источник тока. Использование
управляемого преобразователя
позволяет расширить диапазон
регулирования момента путем увеличения
тока якоря на отдельных этапах
работы электропривода до значений,
допустимых по условиям коммутации.
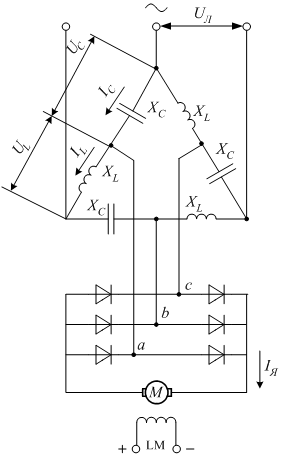
Рисунок
3.26 - Система ИТ-Д
3.8.2
Способы реализации системы ИТ-Д
Однако
наиболее простые схемные решения с
высокими показателями качества
регулирования момента получаются
при использовании параметрических
источников тока, принцип действия
которых основан на явлении резонанса
в цепи переменного тока, содержащей
индуктивные и емкостные элементы.
Известен ряд схем подобных
преобразователей; наиболее
распространенный вариант трехфазной
схемы источника тока для питания
двигателя постоянного тока показан
на рис.
Данная
схема при определенном выборе
параметров обеспечивает стабилизацию
тока нагрузки в широких пределах
изменения противо-ЭДС двигателя,
ограничиваемых только линейностью
и допустимыми током и напряжением
ее элементов, при этом благодаря
симметрии схемы в установившихся
режимах работы можно ограничиться
рассмотрением работы одной фазы.
Ток нагрузки одной фазы при принятых
на схеме направлениях выразится
так:
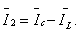
Токи
реактивных элементов схемы определяются
известными соотношениями:
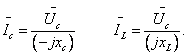
При
xc
= xL=x
соотношение
принимает вид
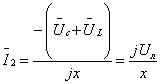 , ,
где
Uл
=
Uс
+ UL
— линейное
напряжение питающей сети.
Так
как выпрямленный ток Id
пропорционален
эффективному значению тока I2,
из
формулы вытекает, что при идеальных
линейных реактивных элементах ток
якоря двигателя не зависит от
противо-ЭДС двигателя и сопротивления
цепи нагрузки и при Uл
=
const
является постоянным: Этот
эффект достигается за счет резонанса
напряжений в контуре, образованном
реактивными элементами благодаря
которому изменение сопротивления
нагрузки R2
сопровождается пропорциональным
изменением приложенного напряжения
к нагрузке U2.
Нагрузка подключается к индуктивно
ёмкостному преобразователю через
выпрямительный мост. В этом случае
можно считать, что Id
= 1,35·I2
=const;
Ud=2,34U2.
При закороченной нагрузке R2=0
(или Ud
=0 -двигатель стоит), напряжения на
резонансных элементах равны фазным
напряжениям сети. Ток I
в этом режиме равен нулю, т. е. из сети
ток не потребляется.
Индуктивно-емкостный
преобразователь обладает высоким
КПД и коэффициентом мощности, близким
к единице. Однако наличие
неуправляемого выпрямителя исключает
возможность рекуперации энергии
в сеть при тормозных режимах работы
двигателя, что снижает управляемость
привода.
Допустимые
границы изменения переменных
отметим, что в данном случае важнейшее
ограничение
по току якоря
выполняется естественно—источником
питания, который для работы в
продолжительном режиме выбирается
так, чтобы Iи.т
<Iном.
Магнитный
поток
в продолжительном режиме также
ограничивается номинальным значением
Ф ≤ Фном,
поскольку Iв.ном
устанавливается, как отмечалось
ранее, по условию допустимого
нагревания обмотки. Кратковременно
можно допустить Iв=
(2—3)Iв.ном
и более, но это не приведет вследствие
насыщения магнитной цепи машины к
заметному росту потока, поэтому даже
кратковременно Мдоп
≤
(1,2÷1,3)Мном,
а в продолжительном режиме Мдоп
≤ Мном.
Ограничение
по напряжению на якоре.
Если принять Uдоп
≤
Uном,
то при
изменении
тока ИТ
и
Ф = Фном
= const
скорость, допустимая по условию
ограничения напряжения, определится
как ωдоп.эл
= Uном/kФном
≈
ωном.
Более благоприятными будут
условия при Iи.т=
Iном=const
и Ф=vаг:
ωдоп.эл
= Uном/kФном
будет
расти с уменьшением потока и
ограничится лишь условиями
механической прочности ωдоп.мех.
Недоиспользование перегрузочной
способности двигателя по току и
моменту оказывает безусловно
положительное влияние на надежность
— гарантируется нормальная коммутация,
нормальный тепловой режим якоря и
т. п. Вместе с тем очевидно, что
снижаются динамические возможности.
При
U1л=380
U1ф=220
изменение напряжения на нагрузке в
диапазоне Ud=U2/
0.44 = 0 - 500В к резонансным элементам
прикладывается напряжение не
превышающее 220 В.
Этот
источник тока позволяет получить
при бестрансформаторном подключении
к трёхфазной сети любые ограниченные
лишь прочностью элементов напряжения
на выходе.
3.8.3
Надежность индуктивно-емкостного
преобразователя (ИЕП)
Специфика
источника тока выразится в первую
очередь, в том, что изменится природа
опасных режимов: если обычным
аварийным режимом является режим
короткого замыкания, то для ИЕП
авария - обрыв цепи нагрузки до или
после выпрямителя, т. е. холостой
ход. При этом резко и быстро растут
напряжения на выходе и ток, потребляемый
из сети.
Одна
из причин ненадёжности - неправильная
фазировка при подключении к сети.
Это приведёт к росту напряжения на
реактивных элементах, насыщению
реакторов, их нагрев. Хотя для нагрузки
это неопасно.
Другая
причина ненадёжности нарушение
условия Хр = Хк. Такой отказ называется
параметрическим, он сопровождается
теми же явлениями, что и неправильная
фазировка.
3.8.4
Примеры применения
ЭП
с управляемым моментом выполненный
по системе ИЕП - В -Д, в силу присущих
ему должен занять промежуточное
положение между простым и дешёвым
нерегулируемым ЭП, выполненным на
короткозамкнутых асинхронных
двигателях и тиристорным ЭЛ постоянного
и переменного тока. Изложенное дает
основание определить некоторые
области эффективного использования
ЭП с управляемым моментом.
• Многодвигательная
система для перемотки нити, ленты
или полосы, в секциях которой
производятся различные технологические
операции - наложение изоляции, её
обработка; снятие окалины; сушка,
окраска и т. п. Такие технологические
линии удобно строить по описанному
выше принципу: один из двигателей
задаёт скорость, другие, соединённые
последовательно с первым, обеспечивают
необходимое натяжение в каждой
секции без каких-либо дополнительных
устройств.
• Барабаны
или шпули, принимающие проволоку
или ленту после обработки, например,
после волочильных станов. Качественная
укладка без заклинивания проволоки
или перекоса ленты.
• Устройства
для намотки с заданным натяжением
различных катушек, обмоток электрических
машин.
• Лебёдки
для буксировки судов на волнах или
для поддержания в натянутом состоянии
ведущего троса при передаче груза
с корабль на корабль в условиях
волнения моря.
• Нагружающие
устройства в установках для испытания
различных двигателей, позволяющие
изменять по программе момент на валу
электродвигателя. 3.9
Реостатный пуск двигателя постоянного
тока независимого возбуждения
3.9.1
Построение пусковой диаграммы
Принципиальная
схема для этого способа пуска
приведена на рис. 3.27. Пуск осуществляется
следующим образом. Предварительно
включается обмотка возбуждения LM,
а затем замыкается контакт KM
и двигатель М разгоняется. По мере
разгона двигателя ступени пускового
реостата R1СТ,
R2СТ
и R3СТ
последовательно шунтируются
соответствующими контактами ускорения
KM1,
KM2
и KM3,
после чего двигатель переходит на
естественную характеристику. При
таком способе пуска необходимо уметь
рассчитывать сопротивления ступеней
пускового реостата. Существуют
графоаналитический и аналитический
методы расчета. Остановимся на
первом, аналитический метод
используется в демонстрации.
При
графоаналитическом методе расчета
вначале строится пусковая диаграмма
(рис. 3.28), т. е. семейство механических
или электромеханических характеристик
при всех положениях пускового
реостата. Для этого по каталожным
данным двигателя строится естественная
характеристика 1 и выбираются величины
максимального момента М1 (или тока
I1)
переключения и минимального М2 (или
I2).
Величина момента М1 (или тока I1)
не должна превышать максимально
допустимые значения для данного
типа двигателей. Ориентировочно для
двигателей средней мощности М1 = (2 ÷
2,5) Мн или I1
= (2 ÷ 2,5) Iн.
Величина момента М2 (или тока I2)
выбирается с учетом возможных
изменений момента сопротивления
механизма и напряжения питающей
сети и обычно берется на 10÷20% больше
момента сопротивления механизма.
Через точки а
и n
(рис. 3.28) проводятся вертикали. Затем
проводится первая реостатная
характеристика в виде прямой,
соединяющей точки а
и ω0. В соответствии с этой характеристикой
ротор двигателя увеличивает скорость
до значения, определяемого точкой
b.
В этот момент шунтируется первая
ступень пускового реостата R1ст
контактом ускорения KM1.
Так
как привод обладает значительным
запасом инерции, то скорость двигателя
не может измениться сразу, а величина
момента (или тока) практически
мгновенно возрастает до значения
М1 (или I1).
Поэтому переход на вторую реостатную
характеристику совершается по
горизонтальной линии bc.
Через точки с
и ω0 проводится вторая реостатная
характеристика и т. д.
Последняя
горизонталь fg
должна пересечь естественную
характеристику в точке f
при моменте М1 (или токе I1).
Если этого не произошло, то необходимо
изменить величину момента М2 (или
тока I2)
и произвести новое построение.
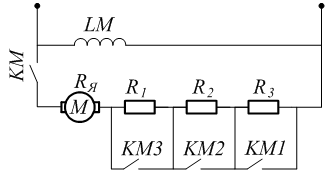
Рисунок
3.27 - Схема реостатного пуска ДПТ
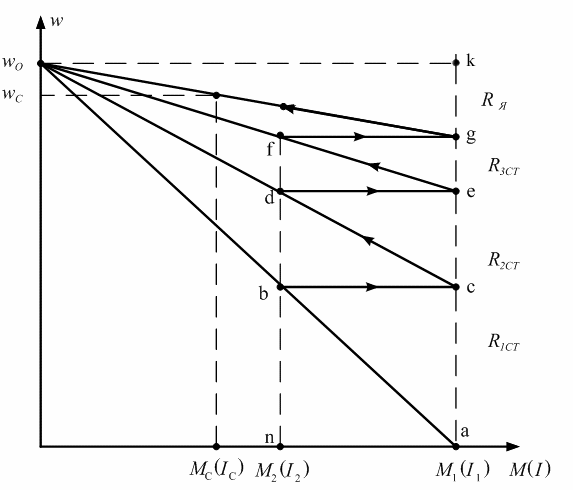
Рисунок
3.28 - Пусковая диаграмма
Число
ступеней пускового реостата обычно
берется от 3 до 5, так как дальнейшее
увеличение числа ступеней нежелательно
из-за возрастания количества
контакторов ускорения.
3.9.2
Расчет пусковых сопротивлений
Согласно
уравнениям (3.10)
и (3.11)
второй член, представляющий перепад
скорости Δω относительно ω0, при
постоянном М = М1 пропорционален
сопротивлению роторной цепи двигателя.
Таким образом, отрезок gk
в определенном масштабе представляет
собой сопротивление ротора двигателя
Rя,
а отрезки ас,
се
и еg
— соответственно сопротивления
ступеней пускового реостата R1ст,
R2ст
и R3ст.
Масштаб
сопротивлений можно найти, исходя
из отрезка gk
и известной величины Rя:
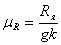 . .
Но,
так как сопротивление Rя
может иметь небольшую величину, это
вызовет значительную погрешность
в расчетах. Поэтому масштаб
сопротивлений обычно находят из
суммарного сопротивления всей
роторной цепи
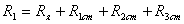 ,
как ,
как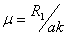 ,
где ,
где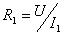 . .
Тогда
сопротивления ступеней пускового
реостата определятся следующим
образом:
 , ,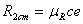 , ,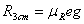 . .
Чтобы
выяснить, как происходит изменение
момента, тока и скорости от времени
при ступенчатом пуске двигателя,
можно воспользоваться уравнениями,
полученными при пуске двигателя
непосредственным включением в сеть,
но при других начальных условиях,
которые определяются в момент времени
t=
0 для каждой ступени.
Такой
процесс пуска характерен тем, что
момент (или ток) двигателя во время
пуска колеблется в пределах от М1
(или I1)
до М2 (или I2).
В начале пуска, на первой реостатной
характеристике, в момент времени t=
0 (точка а, рис. 3.28) М1 = Мнач= Мк.з.
(или I1
= Iнач=
Iк.з.),
затем по мере разгона двигателя
момент (или ток) двигателя уменьшается
до значения М = М2 (или I=
I2)
в точке b.
Для
лучшего усвоения материала и
ознакомления с аналитическим способом
построения пусковой диаграммы и
расчета сопротивлений посмотрите
демонстрацию
|
|

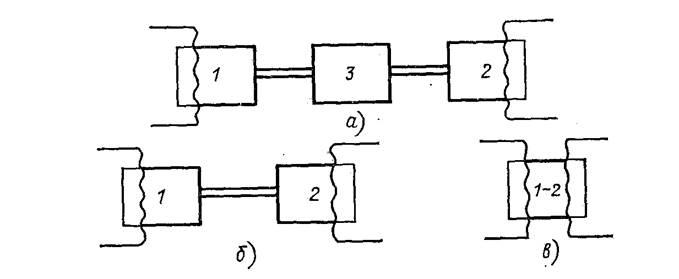

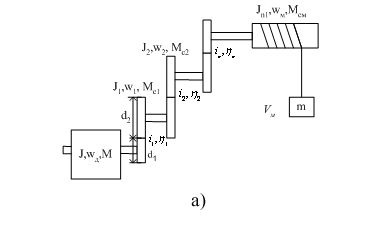
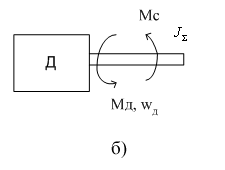
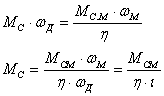 (2.3)
(2.3)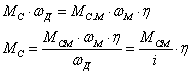
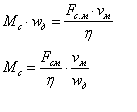
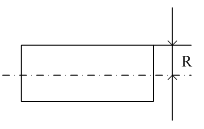
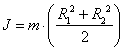
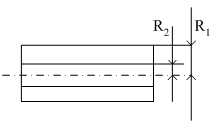


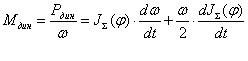
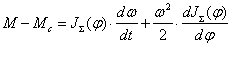 (2.14)
(2.14)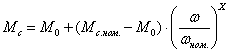







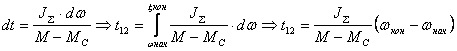 (2.15)
(2.15)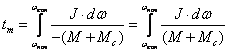

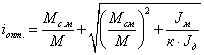
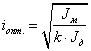

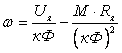 .
(3.6)
.
(3.6)

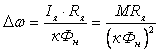 .
(3.10)
.
(3.10)
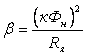 .
(3.13)
.
(3.13)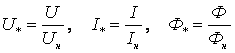 ,
,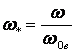 -
относительное значение скорости;
-
относительное значение скорости;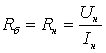
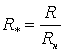 ;
; ;
;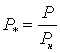 ;
;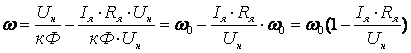
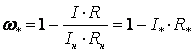 ;
;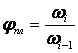 ,
,
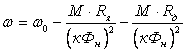 ;
;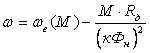 ,
,
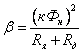 снижается
по мере уменьшения скорости.
снижается
по мере уменьшения скорости.
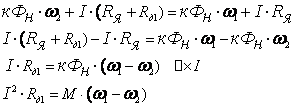




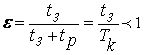 .
.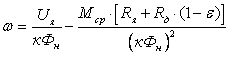 ,
,

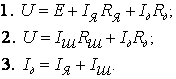
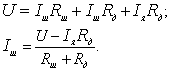
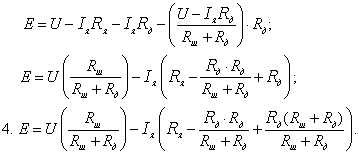
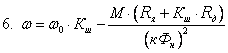 .
.


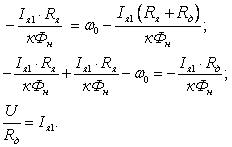
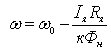 .
.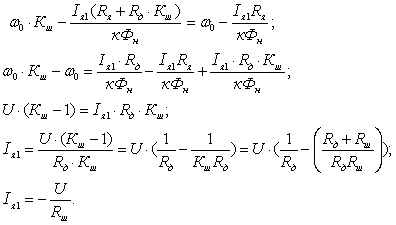
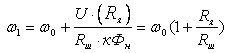 .
.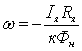 .
.







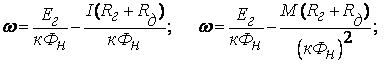

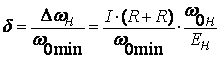 .
.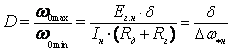 .
.

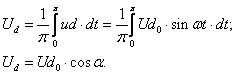
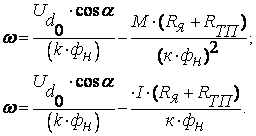








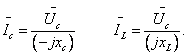
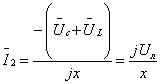 ,
,
