
Консультации
Если в процессе работы над изучением теоретического материала или при решении задач у студента возникают вопросы, разрешить которые самостоятельно не удается (неясность терминов, формулировок теорем, отдельных задач и др.) Студент может обратиться к преподавателю для получения консультации.
На консультации студенту необходимо точно формулировать, в чем он испытывает затруднение. Если он не разобрался в теоретических объяснениях или в выводе формулы по учебнику, то нужно указать, название и автора учебника, год его издания и страницу, где рассмотрен затрудняющий его вопрос. Если студент испытывает затруднение при решении задачи, то следует указать характер этого затруднения и привести предполагаемый вариант решения.
Контрольные работы
Рецензии преподавателя на контрольные работы позволяют студенту судить о степени усвоения им соответствующего раздела курса, указывают на имеющиеся у него пробелы и помогают сформулировать вопросы для постановки их перед преподавателем на консультации.
Следует приступать к выполнению контрольных заданий после изучения теоретического материала и приобретения навыков решения соответствующих задач.
При подготовке к выполнению контрольной работы студент может использовать общие рекомендации по работе над курсом математики.
4. При выполнении контрольных работ нужно соблюдать следующие требования
1) контрольная работа выполняется в тетради (оформление титульного листа см.
приложение);
2) задания выполняются строго по порядку, каждое задание – с новой
страницы;
3) текст каждой задачи переписывается в тетрадь. Решение сопровождается
краткими пояснениями;
4) чертежи выполняются с помощью линейки и карандаша;
5) работа над ошибками выполняется в той же тетради после заголовка «Работа над
ошибками».
Контрольная работа №1.
Задание № 1.Найти разность множествA B иA B.
1.1 A = {x| x Z, – 3 < x ≤ 2}, B = {x| x = 2n – 4, n Î N, n ≤ 4};
1.2 A = {x| x Z, – 2 < x ≤ – 1}, B = {x| x = – 2n, n Î N, n ≤ 5};
1.3 A = {x| x= 2n – 1, n Î N, n < 5}, B = {x| x Î N, 0 < x < 6};
1.4 A = {x| x= n, n Î N, n ≤ 5}, B = {x| x Î Z, 0 ≤ x < 1};
1.5 A = {x| x= n + 1, n Î N, 3 ≤ n ≤ 7}, B = {x| x Î N, 4 ≤ x ≤ 6};
1.6 A = {x| x Î Z, – 2 ≤ x < 0}, B = {x| x = 3n, n Î N, n ≤ 5};
1.7 A = {x| x= 2n + 1, n Î N, 2 ≤ n ≤ 4}, B = {x| x Î N, 5 ≤ x ≤ 9};
1.8 A = {x| x= n2, n Î N, n ≤ 5}, B = {x| x Î Z, 1 < x < 4};
1.9 A = {x| x= n – 2, n Î N, n ≤ 5}, B = {x| x Î Z, – 3 ≤ x ≤ 0};
1.10 A = {x| x= 5n, n Î N, n ≤ 3}, B = {x| x Î Z, 0 ≤ x < 5};
1.11 A = {x| x= 3 – n, n Î N, 2 ≤ n ≤ 5}, B = {x| x Î Z, – 5 ≤ x < 0};
1.12 A = {x| x= n2 – 5, n Î N, n < 6}, B = {x| x Î N, 0 ≤ x < 4};
1.13 A = {x| x Î Z, 2 ≤ x ≤ 6}, B = {x| x = 2n, n Î N, n ≤ 2};
1.14 A = {x| x= n2 – 7, n Î N, n ≤ 4}, B = {x| x Î Z, – 3 < x < 2};
1.15 A = {x| x= n2 + 1, n Î N, n < 3}, B = {x| x Î N, 2 ≤ x ≤ 6};
1.16 A = {x| x= – 5 n, n Î N, 3 ≤ x < 8}, B = {x| x Î Z, – 25 < x < – 20};
1.17 A = {x| x= 2n – 7, n Î N, n ≤ 5}, B = {x| x Î Z, – 8 < x < – 3};
1.18 A = {x| x Î N, 0 ≤ x ≤ 1}, B = {x| x = 3n – 5, n Î N, n < 6};
1.19 A = {x| x= n2 – 3, n Î N, 3 ≤ n < 7}, B = {x| x Î N, 6 < x ≤ 12};
1.20 A = {x| x= 1 – 3n, n Î N, 3 ≤n ≤ 7}, B = {x| x Î Z, – 15 < x ≤ – 14}.
Задание № 2.Изобразить на координатной плоскости декартово произведение множествXи Y.
2.1 X = {2, 4, 6}, Y = {1, 3}; 2.6 X = {– 3} Y = R;
2.2 X = [1, 2], Y = [0, 1]; 2.7 X = [– 3, 2], Y = 1;
2.3 X = (– 1, 1), Y = (– 1, 0); 2.8 X = { – 2} Y = [– 3, 2];
2.4 X = (– 2, 3), Y = [– 4, 1]; 2.9 X = {0} Y = (0, + );
2.5 X = R, Y = {4}; 2.10 X = R, Y = (–,– 3];
2.11 X = (0, + ¥), Y = (–, 0);2.16X = R,Y = {– 3,– 2};
2.12 X = (–, 1], Y = R; 2.17X = {2, 4, 6},Y = (1, 3];
2.13 X = [1, 4], Y = (2, 6); 2.18X = [2, 4],Y = {0,1, 2};
2.14 X = (–¥,– 1); Y = {– 1}; 2.19X = {1, 3, 5},Y = (–1,1);
2.15 X = {1, 2},Y = R;2.20 X = {4},Y = {4}.
Задание № 3.Решить систему уравнений: а) по формулам Крамера;
б) методом Гаусса;
в) матричным методом.
3.1
 3.7
3.7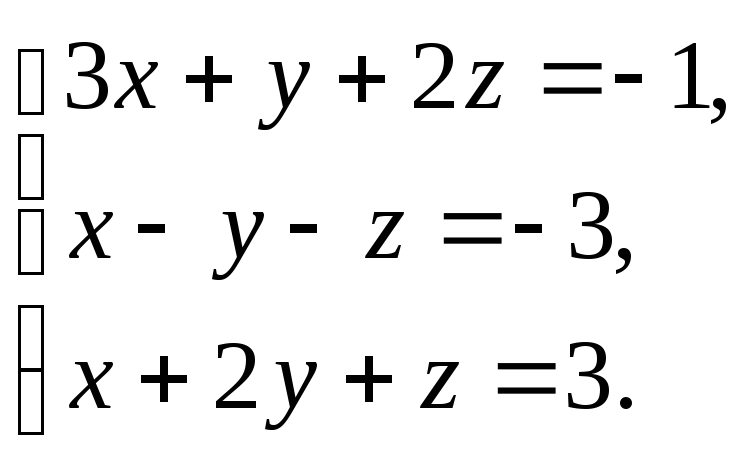
3.2
 3.8
3.8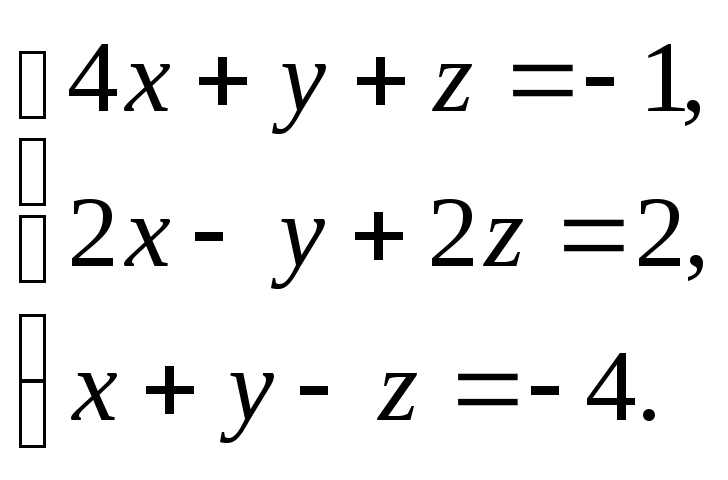
3.3
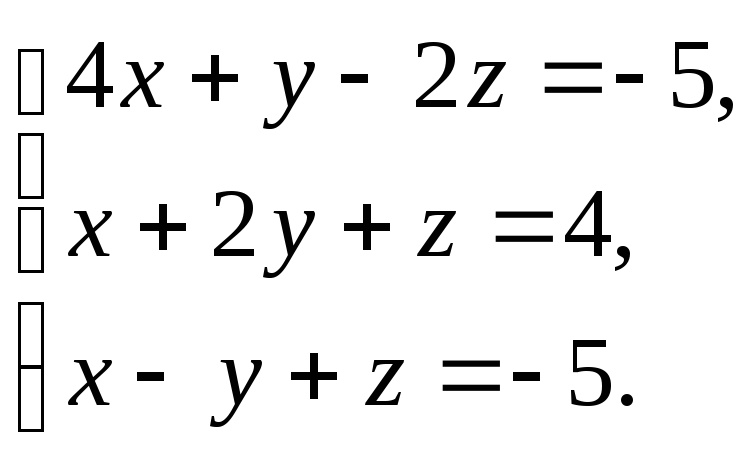 3.9
3.9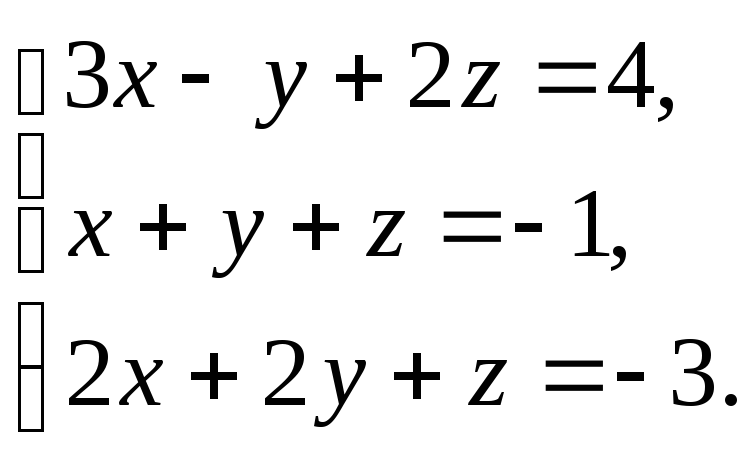
3.4
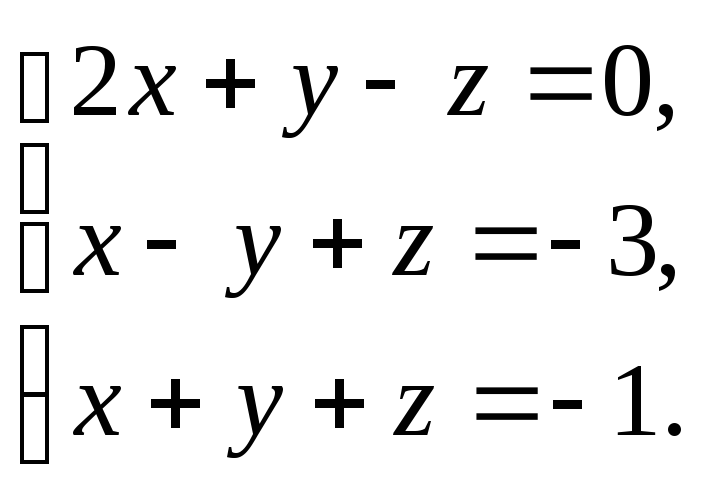 3.10
3.10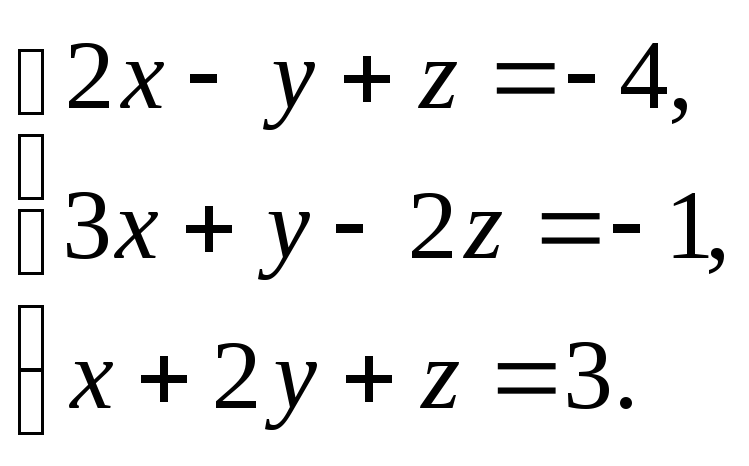
3.5
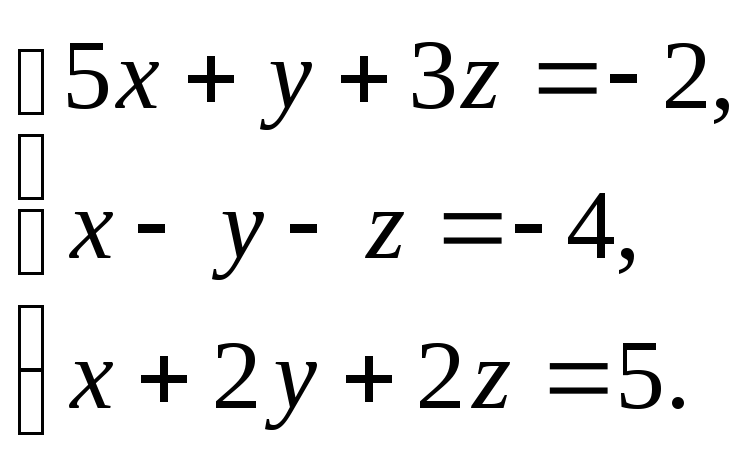 3.11
3.11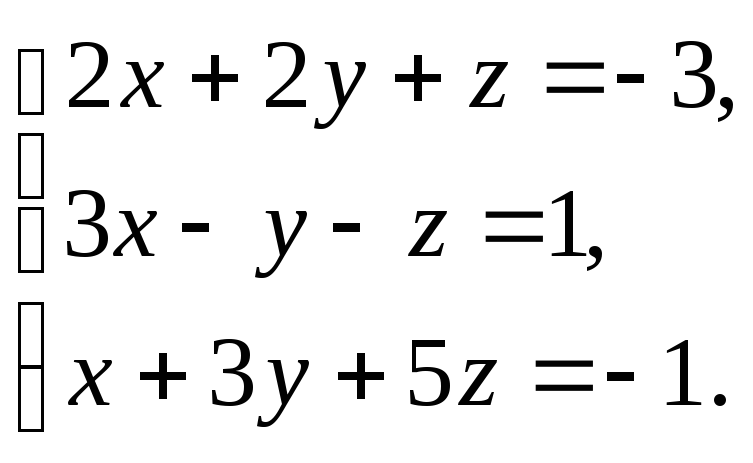
3.6
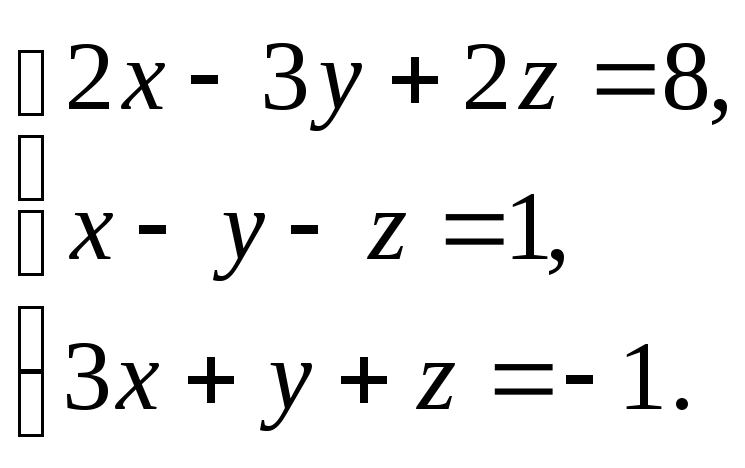 3.12
3.12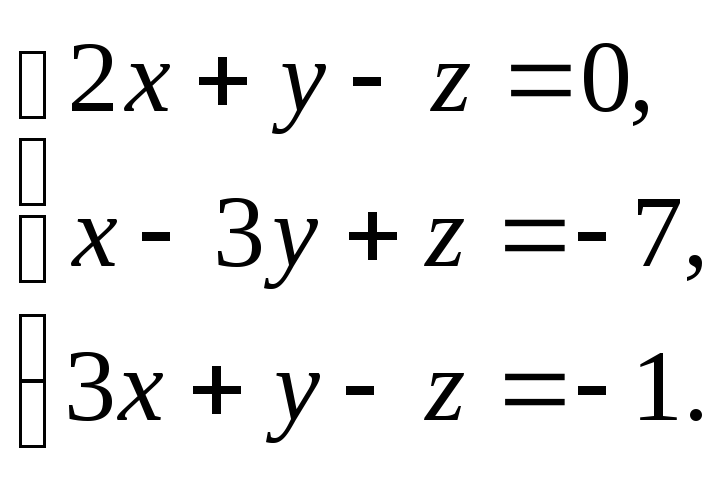
3.13
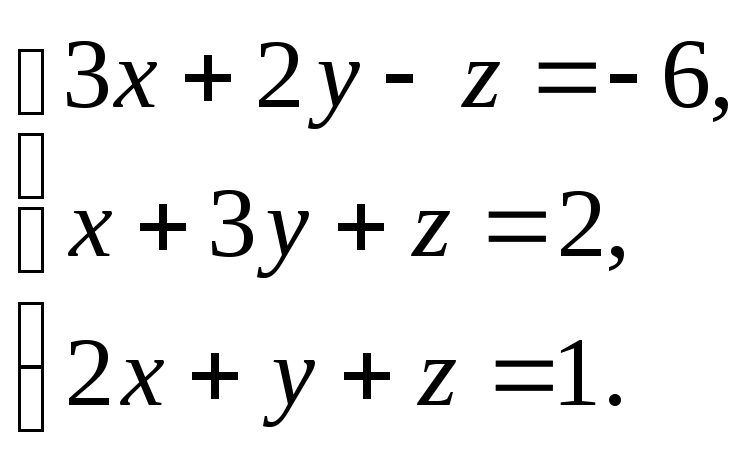 3.17
3.17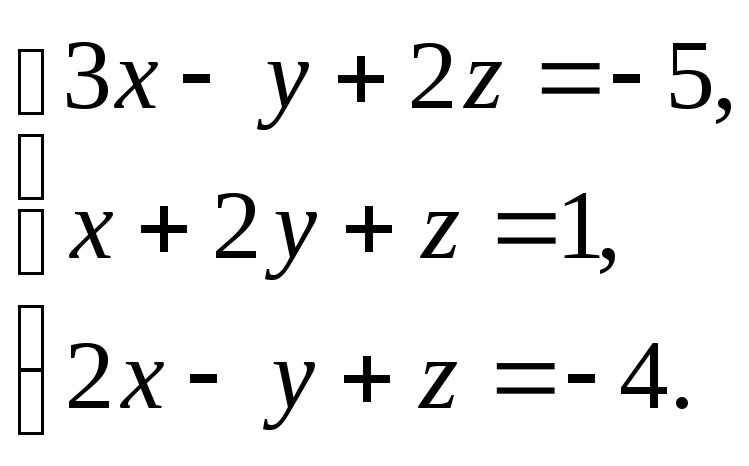
3.14
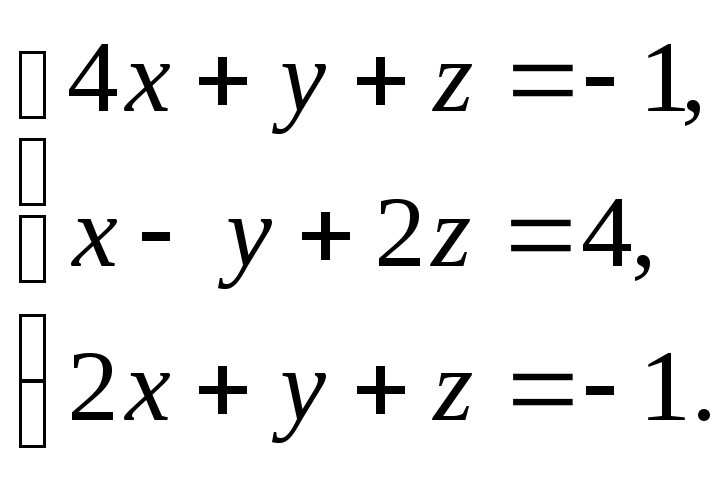 3.18
3.18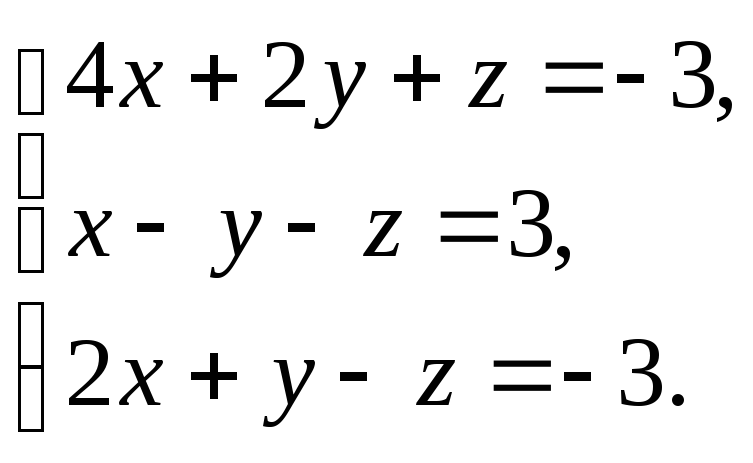
3.15
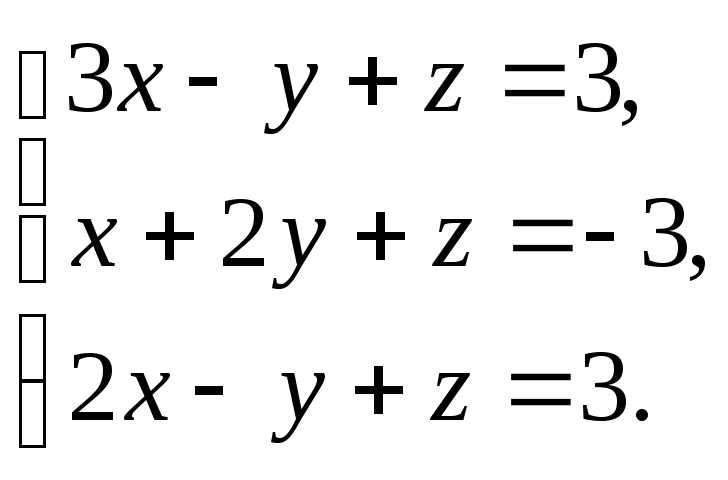 3.
19
3.
19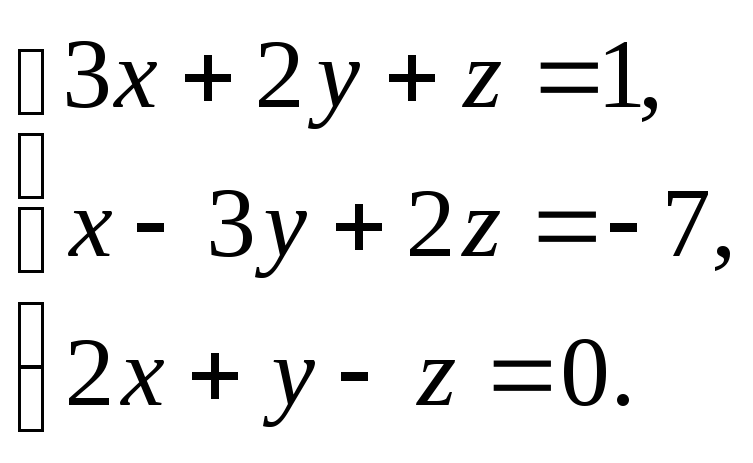
3.16
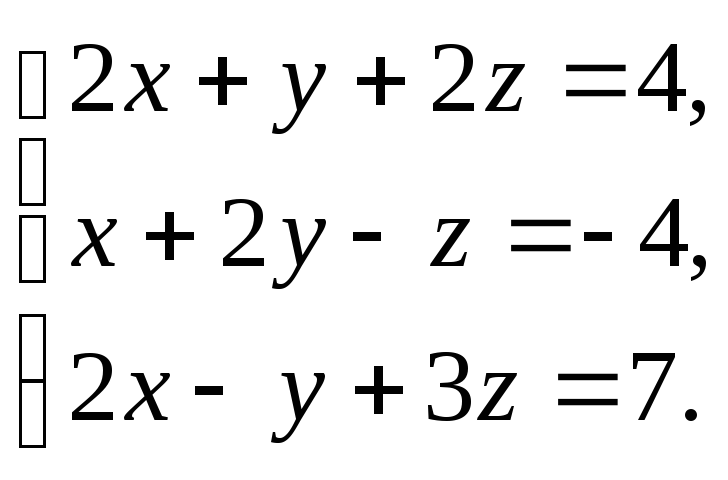 3.
20
3.
20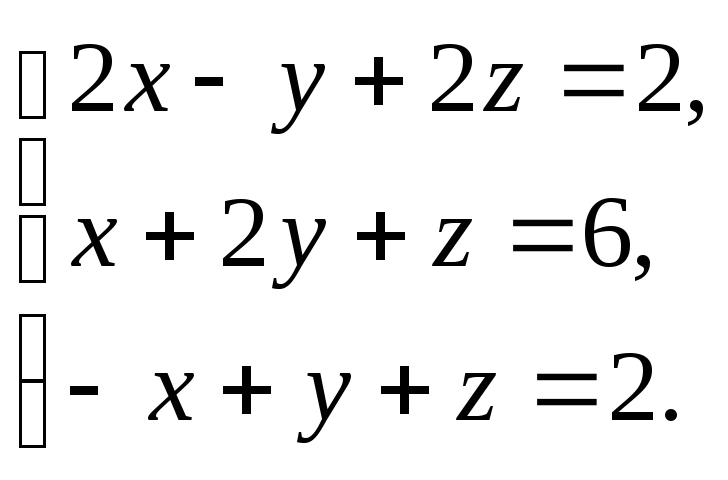
Задание № 4.Даны векторы![]() .
.
Найти: 1) площадь треугольника,
построенного на векторах
![]() и
и![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() .
.
4.1
![]() ,
,![]() ,
,![]() ;
;
4.2
![]() ,
,![]() ,
,![]() ;
;
4.3
![]() ,
,![]() ,
,![]() ;
;
4.4
![]() ,
,![]() ,
,![]() ;
;
4.5
![]() ,
,![]() ,
,![]() ;
;
4.6
![]() ,
,![]() ,
,![]() ;
;
4.7
![]() ,
,![]() ,
,![]() ;
;
4.8
![]() ,
,![]() ,
,![]() ;
;
4.9
![]() ,
,![]() ,
,![]() ;
;
4.10
![]() ,
,![]() ,
,![]() ;
;
4.11
![]() ,
,![]() ,
,![]() ;
;
4.12
![]() ,
,![]() ,
,![]() ;
;
4.13
![]() ,
,![]() ,
,![]() ;
;
4.14
![]() ,
,![]() ,
,![]() ;
;
4.15
![]() ,
,![]() ,
,![]() ;
;
4.16
![]() ,
,![]() ,
,![]() ;
;
4.17
![]() ,
,![]() ,
,![]() ;
;
4.18
![]() ,
,![]() ,
,![]() ;
;
4.19
![]() ,
,![]() ,
,![]() ;
;
4.20
![]() ,
,![]() ,
,![]() .
.
Задание № 5.Найти область определения функции.
5.1
![]() ; 5.10
; 5.10
![]() ;
;
5.2
![]() ; 5.11
; 5.11![]() ;
;
5.3
![]() ; 5.12
; 5.12
![]() ;
;
5.4
![]() ; 5.13
; 5.13
![]() ;
;
5.5
![]() ; 5.14
; 5.14
![]() ;
;
5.6
![]() ; 5.15
; 5.15
![]() ;
;
5.7
![]() ; 5.16
; 5.16
![]() ;
;
5.8
![]() ; 5.17
; 5.17
![]() ;
;
5.9
![]() ; 5.18
; 5.18
![]() ;
;
5.19
![]() ; 5.20
; 5.20
![]() .
.
Задание № 6.Вычислить пределы, не используя правило Лопиталя.
6.1. 1)
![]() ; 6.3 1)
; 6.3 1)
![]() ;
;
2)
![]() ;2)
;2)
![]() ;
;
3) ![]() ; 3)
; 3)
![]() ;
;
4) ![]() ;4)
;4)
![]() ;
;
5) ![]() ;5)
;5)
![]() ;
;
6)
![]() .6)
.6)
![]() .
.
6.2 1)
![]() ; 6.4 1)
; 6.4 1)
![]() ;
;
2)
![]() 2)
2)
![]() ;
;
3) ![]() ; 3)
; 3)
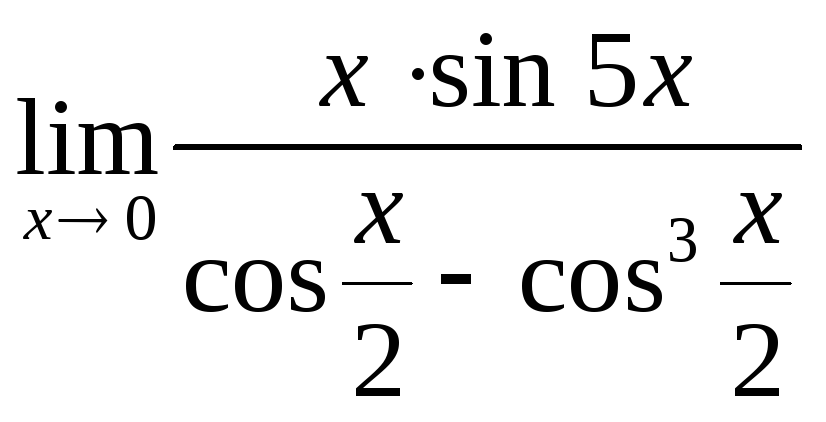 ;
;
4) ![]() ;4)
;4)
![]() ;
;
5) ![]() ;5)
;5)
![]() .
.
6)
![]() . 6)
. 6)![]()
6.5 1) ![]() ; 6.6 1)
; 6.6 1)
![]() ;
;
2) ![]() ;2)
;2)
![]() ;
;
3)
![]() ;3)
;3)
![]() ;
;
4) ![]() ;4)
;4)
![]() ;
;
5)
![]() ;5)
;5)
![]() ;
;
6) ![]() . 6)
. 6)
![]() .
.
6.7 1) ![]() ; 6.10 1)
; 6.10 1)
![]() ;
;
2) ![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 3)
; 3)![]() ;
;
4) ![]() ; 4)
; 4)
![]() ;
;
5)
![]() ; 5)
; 5)
![]() ;
;
6) ![]() . 6)
. 6)
![]() .
.
6.8 1)
![]() ; 6.11 1)
; 6.11 1)
![]() ;
;
2)
![]() ;2)
;2)![]() ;
;
3) ![]() ; 3)
; 3)
![]() ;
;
4) ![]() ;4)
;4)
![]() ;
;
5) ![]() ;5)
;5)
![]() ;
;
6) ![]() . 6)
. 6)
![]() .
.
6.9 1)
![]() ; 6.12 1)
; 6.12 1)
![]() ;
;
2)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 3)
; 3)
![]() ;
;
4) 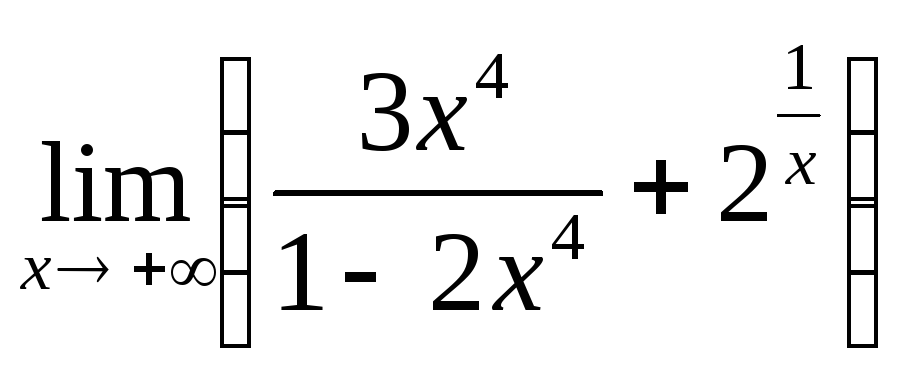 ; 4)
; 4)
![]()
5) ![]() . 5)
. 5)
![]() .
.
6) ![]() 6)
6)
![]()
6.13. 1) ![]() ; 6.16 1)
; 6.16 1)
![]() ;
;
2)
![]() ;2)
;2)
![]() ;
;
3) ![]() ; 3)
; 3)
![]() ;
;
4)
![]() ;4)
;4)
![]() ;
;
5) ![]() ;5)
;5)
![]() .
.
6) ![]() . 6)
. 6)
![]() ;
;
6.141)
![]() ; 6.17 1)
; 6.17 1)
![]() ;
;
2) ![]() ;2)
;2)
![]() ;
;
3) ![]() ; 3)
; 3)
![]() ;
;
4)
![]() ;4)
;4)
![]() ;
;
5) ![]() ;5)
;5)
![]() ;
;
6) ![]() . 6)
. 6)
![]() .
.
6.151)
![]() ; 6.18. 1)
; 6.18. 1)
![]() ;
;
2)
![]() ;2)
;2)
![]() ;
;
3) ![]() ; 3)
; 3)
![]() ;
;
4) ![]() ;4)
;4)
![]() ;
;
5)
![]() ;5)
;5)
![]() ;
;
6) ![]() . 6)
. 6)
![]() .
.
6.19 1).![]() ; 6.20 1)
; 6.20 1)
![]() ;
;
2) ![]() ;2)
;2)
![]() ;
;
3)
![]() ;3)
;3)
![]() ;
;
4) ![]() ;4)
;4)
![]() ;
;
5) ![]() . 5)
. 5)
![]() .
.
Задание № 7.Найти производную функции.
7.1 1)
![]() ; 7.4 1)
; 7.4 1)
![]() ;
;
2)
![]() ; 2)
; 2)![]() ;
;
3)
![]() ;3)
;3)
![]() ;
;
7.2 1)
![]() ; 7.5 1)
; 7.5 1)
![]() ;
;
2)
![]() ; 2)
; 2)![]() ;
;
3)
![]() ; 3)
; 3)![]() ;
;
7.3 1)
![]() ; 7.6 1)
; 7.6 1)
![]() ;
;
2)
![]() ; 2)
; 2)![]() ;
;
3)
![]() ; 3)
; 3)![]() ;
;
7.7 1)
![]() ; 7.12 1)
; 7.12 1)
![]() ;
;
2)
![]() ; 2)
; 2)![]() ;
;
3)
![]() ; 3)
; 3)![]() ;
;
7.8 1)
![]() ; 7.13 1)
; 7.13 1)![]() ;
;
2)
![]() ; 2)
; 2)![]() ;
;
3)
![]() ; 3)
; 3)![]() ;
;
7.9 1)
![]() ; 7.14 1)
; 7.14 1)
![]() ;
;
2)
![]() ; 2)
; 2)![]() ;
;
3)
![]() ; 3)
; 3)
![]() ;
;
7.10 1)
![]() ; 7.15 1)
; 7.15 1)
![]() ;
;
2)
![]() ; 2)
; 2)![]() ;
;
3)
![]() ; 3)
; 3)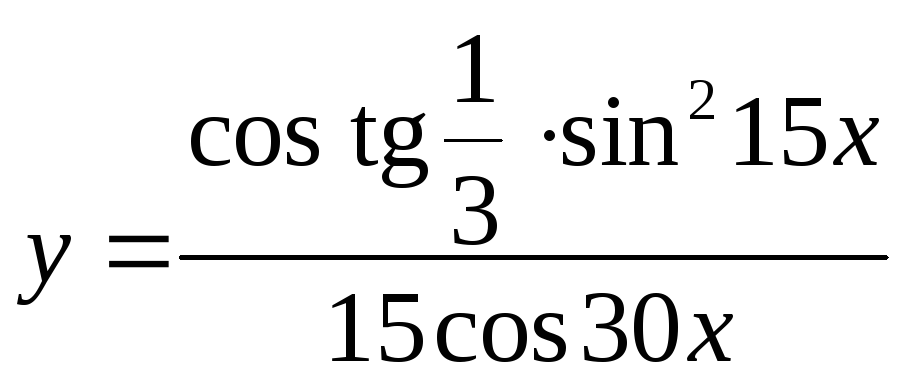 ;
;
7.111)
![]() ; 7.16 1)
; 7.16 1)
![]() ;
;
2)
![]() ; 2)
; 2)![]() ;
;
3)
![]() ; 3)
; 3)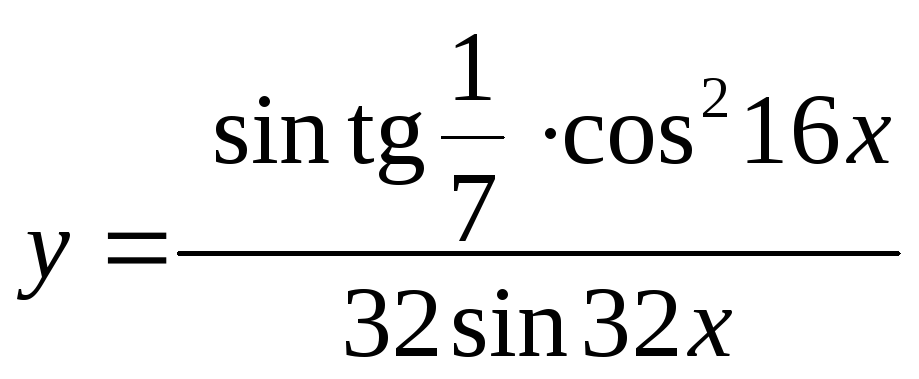 ;
;
7.17 1)
![]() ; 7.19 1)
; 7.19 1)![]() ;
;
2)
![]() ; 2)
; 2)![]() ;
;
3)
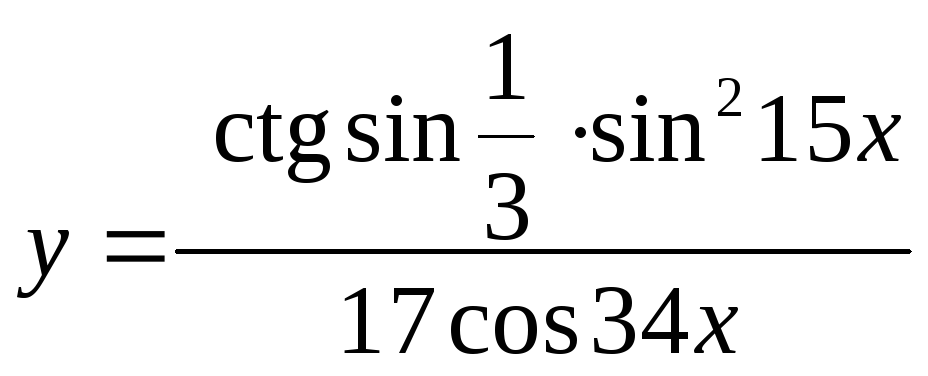 ; 3)
; 3)![]() ;
;
7.18 1)
![]() ; 7.20 1)
; 7.20 1)
![]() ;
;
2)
![]() ; 2)
; 2)![]() ;
;
3)
![]() ; 3)
; 3)![]() .
.
Задание № 8. Найти дифференциал функции.
8.1 ![]() ; 8.11
; 8.11![]() ;
;
8.2 ![]() ; 8.12
; 8.12![]() ;
;
8.3 ![]() ; 8.13
; 8.13![]() ;
;
8.4 ![]() ; 8.14
; 8.14![]() ;
;
8.5 ![]() ; 8.15
; 8.15![]() ;
;
8.6 ![]() ; 8.16
; 8.16![]() ;
;
8.7 ![]() ; 8.17
; 8.17![]() ;
;
8.8 ![]() ; 8.18
; 8.18![]()
8.9 ![]() ; 8.19
; 8.19![]() ;
;
8.10 ![]() ; 8.20
; 8.20![]() .
.
Задание № 9.Задана функцияy = f (x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
9.1 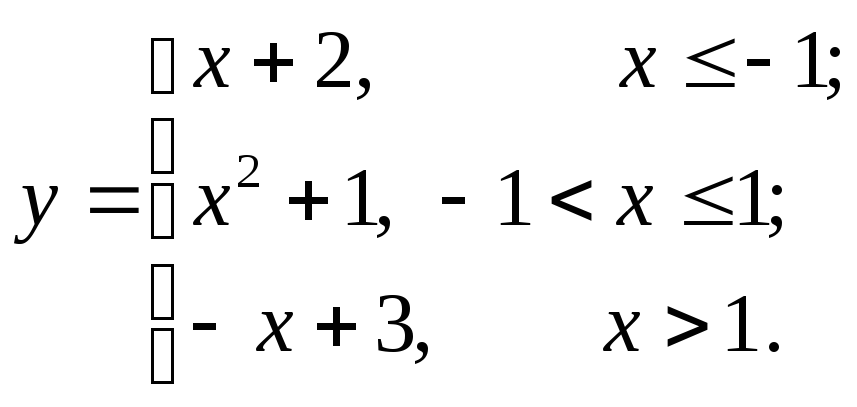 9.8
9.8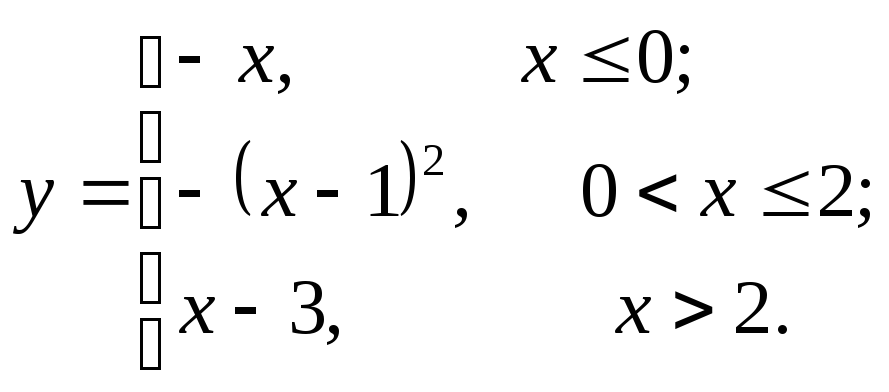
9.2 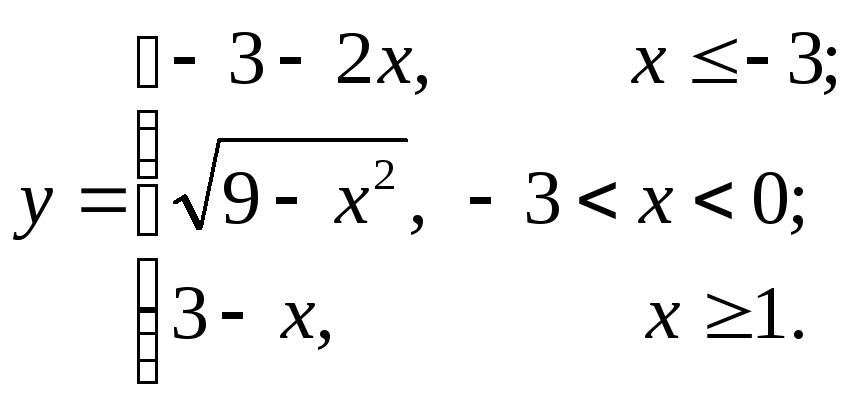 9.9
9.9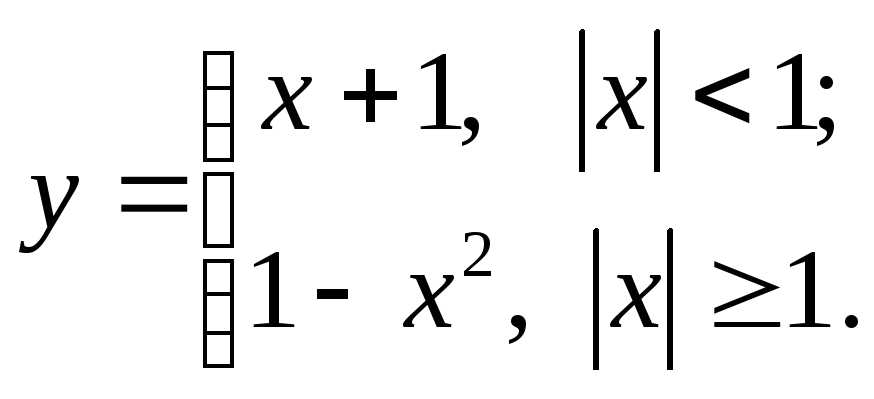
9.3 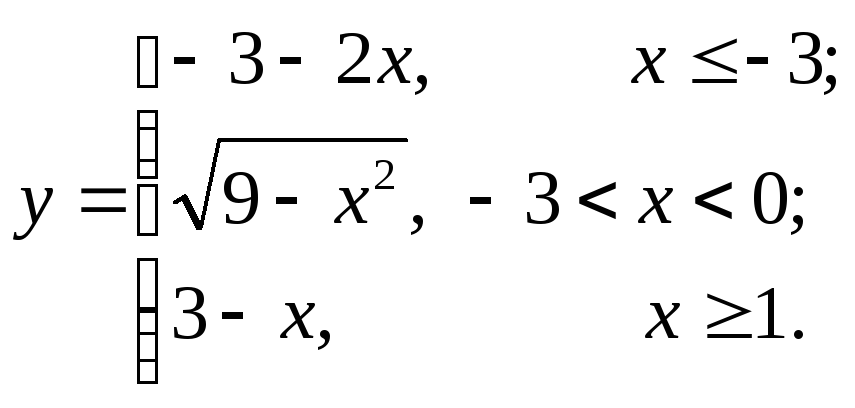 9.10
9.10
9.4  9.11
9.11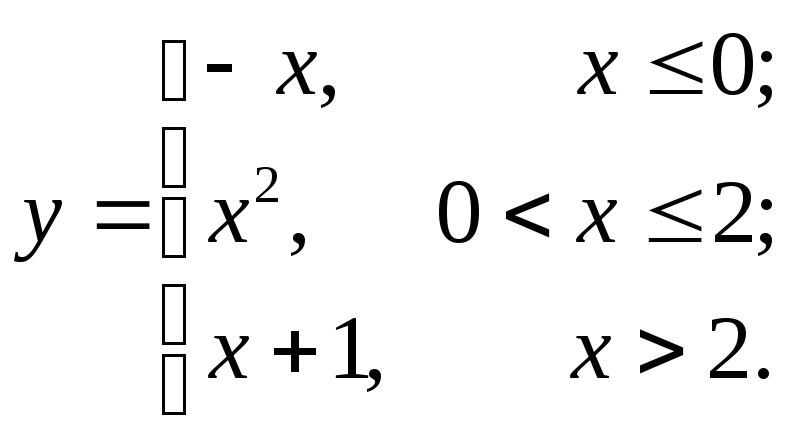
9.5 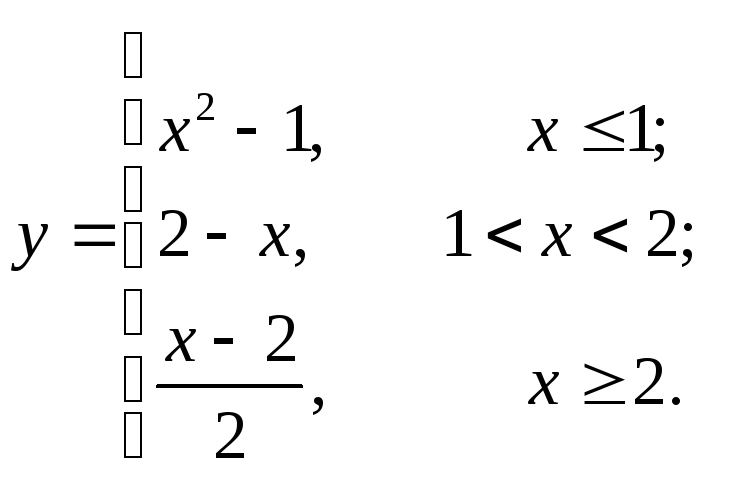 9.12
9.12
9.6 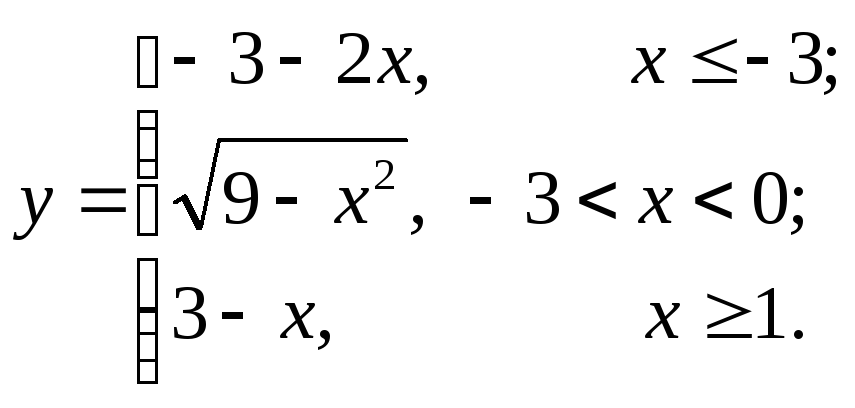 9.13
9.13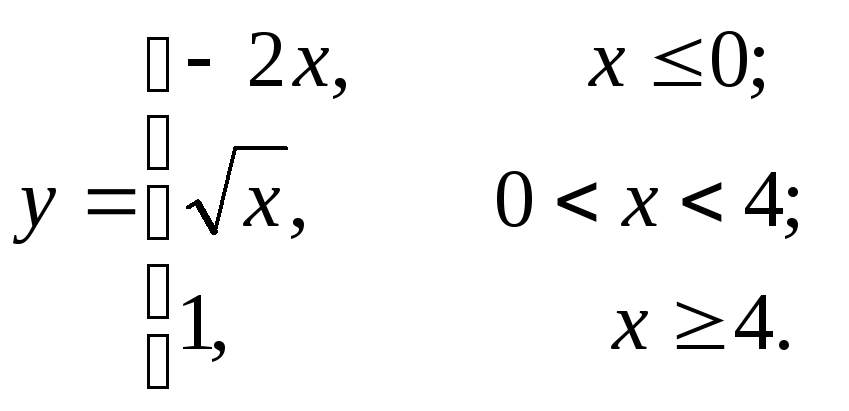
9.7 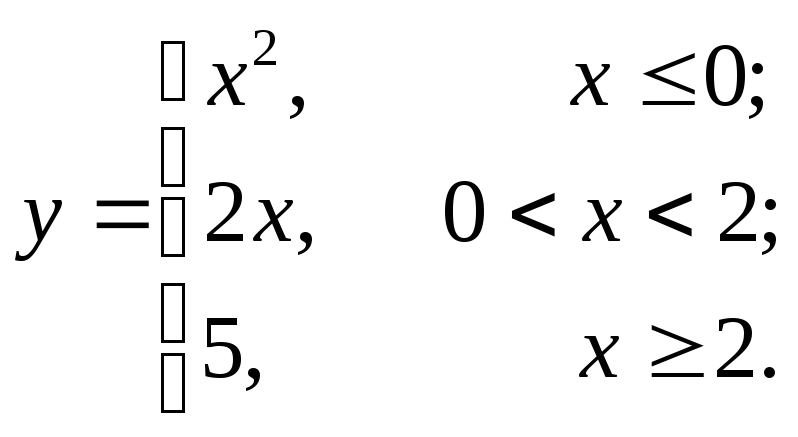 9.14
9.14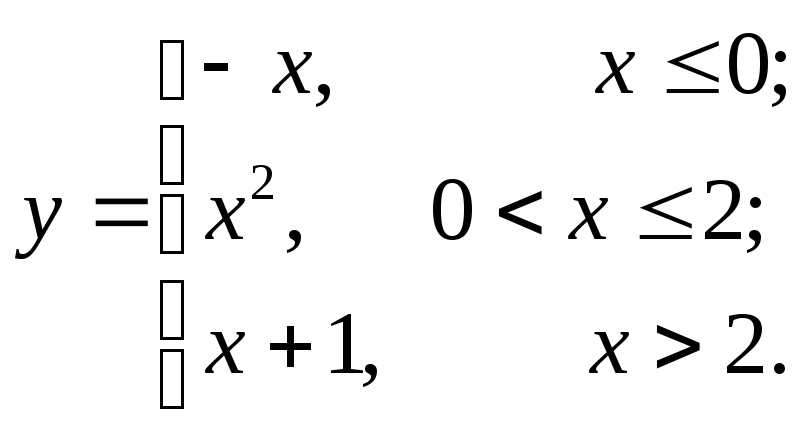
9.15 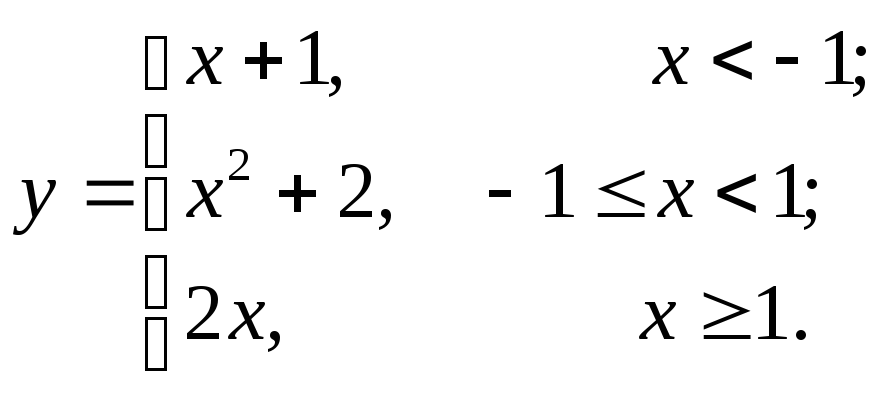 9.18
9.18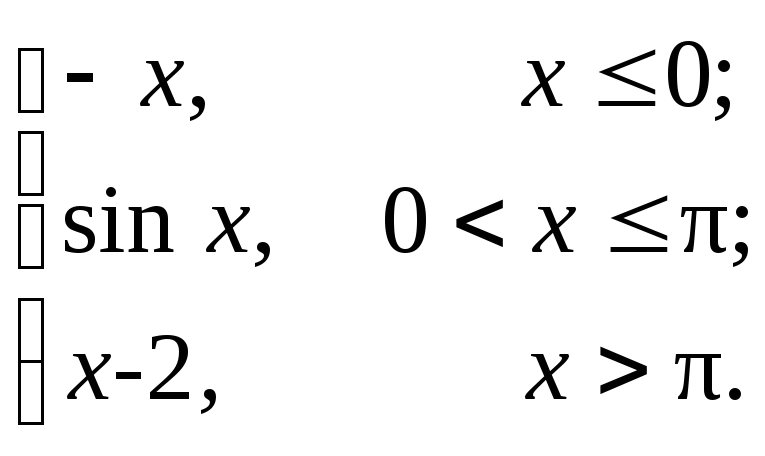
9.16 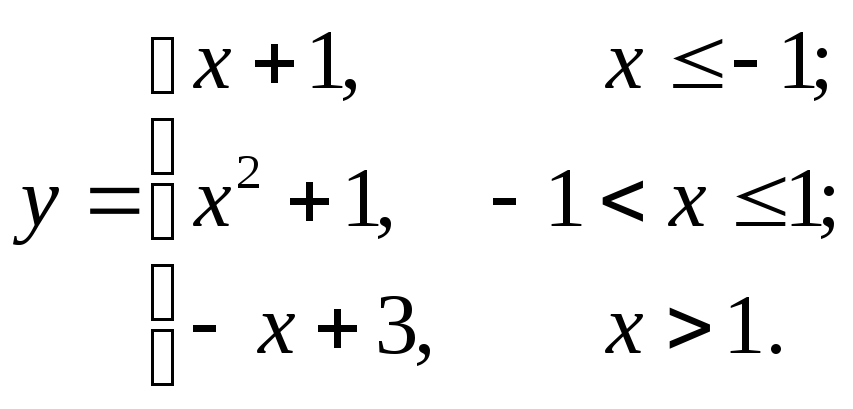 9.19
9.19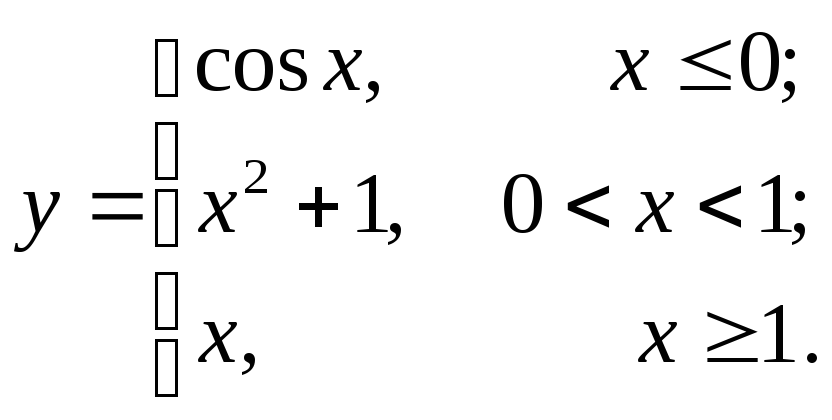
9.17 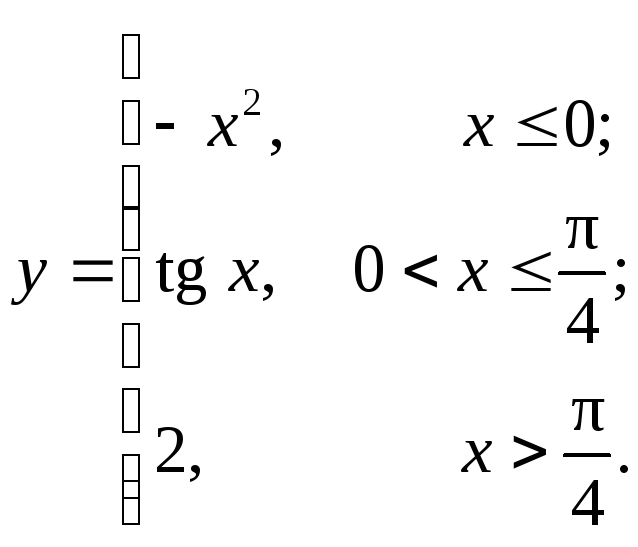 9.20
9.20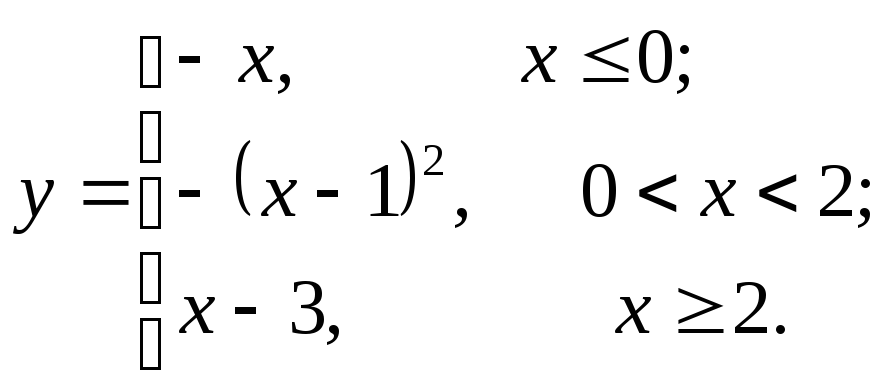
Задание № 10.Провести полное исследование функции и построить ее график.
10.1 ![]() ; 10.8
; 10.8 ![]() ; 10.15
; 10.15 ![]() ;
;
10.2 ![]() ; 10.9
; 10.9 ![]() ; 10.16
; 10.16 ![]() ;
;
10.3 ![]() ; 10.10
; 10.10 ![]() ; 10.17
; 10.17 ![]() ;
;
10.4 ![]() ; 10.11
; 10.11 ![]() ; 10.18
; 10.18 ![]() ;
;
10.5 ![]() ; 10.12
; 10.12 ![]() ; 10.19
; 10.19 ![]() ;
;
10.6 ![]() ; 10.13
; 10.13 ![]() ; 10.20
; 10.20 ![]() .
.
10.7 ![]() ; 10.14
; 10.14 ![]() ;
;
