
- •43. Означення та властивості таких чотирикутників як: прямокутник, ромб, квадрат.
- •44.Трикутник вписаний в коло і описаний навколо нього.
- •45. Чотирикутник вписаний в коло і описаний навколо нього.
- •58. Основні способи доведення теорем. Аналітичний і синтетичний способи доведення теорем.
- •60.Основні способи доведення теорем. Метод доведення від супротивного. Пропедевтика доведень в початковому курсі математики.
- •59.Основні способи доведення геометричних тверджень. Метод вичерпування або повної індукції.
- •59.Основні способи доведення геометричних тверджень. Метод вичерпування або повної індукції.
- •S1 має ознака р
- •7. Питання Знаходження нсд чисел за алгоритмом Евкліда.
- •8 Питання . Прості і складені числа. Побудова таблиці простих чисел.
- •9. Питання Теорема про існування простого дільника у довільного натурального числа більшого за 1 (з доведенням).
- •Доведення:
- •1 Випадок:
- •2 Випадок:
- •22. Числова нерівність. Правильні числові нерівності. Властивості правильних числових нерівностей (Доведення за вибором студента).
- •35. Поняття функції. Область визначення і множина значень функції. Способи задання функції. Графік функції.
- •39. Поняття про геометричну фігуру. Найпростіші геометричні фігури: точка, пряма, площина. Відрізок, промінь, ламана. Довжина ламаної та різні способи її обчислення.
- •40. Кут. Види кутів. Бісектриса кута.
- •41. Трикутник та його елементи. Види трикутників. Найважливіші властивості трикутника. Єгипетський трикутник.
- •42. Означення та властивості таких чотирикутників як: паралелограм, трапеція.
- •43. Означення та властивості таких чотирикутників як: прямокутник, ромб, квадрат.
- •44. Трикутник вписаний в коло і описаний навколо нього.
- •53. Основні задачі на побудову на площині: побудова трикутника за трьома заданими сторонами.
- •54. Охарактеризувати загальну схему розв’язування задач на побудову: аналіз – побудова – доведення – дослідження. Геометричне місце точок як основний метод розв’язування задач на побудову.
- •18. Рівносильні рівняння. Сформулювати та довести теорему 1 про рівносильні рівняння.
8 Питання . Прості і складені числа. Побудова таблиці простих чисел.
Означення:
Числа які діляться тільки самі на себе і на 1 назив. простими.
Натуральне число а назив. складеним , якщо воно має більше двох різних дільників.(12;36;102)
Число 1 має тільки один дільник, це одне саме число, а тому його не відносять ні до простих, ні до складених.
Число 1 яке є не простим, ні складеним, викреслюють , в кружечок після числа 2 викреслюють і обводять в кружечок після 2 третє число 3 , обводять в кружечок число 3 і далі викреслюють число 3 тобто через 2, обводять число 5 і викреслюють п’яте число і.т.д.
Таблиця простих чисел від 1 до 100
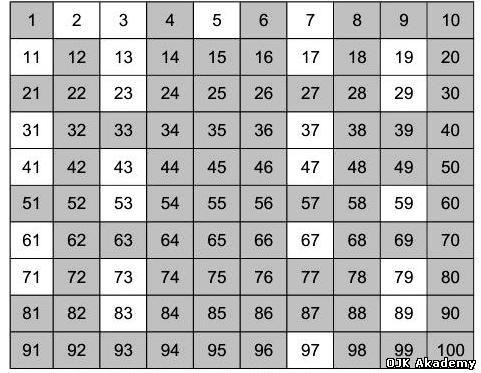
То что белое обводим в кружочек , то что серое вычеркиваем.
Прості числа: 2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97.
9. Питання Теорема про існування простого дільника у довільного натурального числа більшого за 1 (з доведенням).
Довільне натуральне число більше за 1, має принайми хоч би 1 простий дільник.
Дано: ∀ n ∈ N , n>1.
Довести: ∃ р - просте число, n : p
Доведення:
Припустимо : « Що існують такі натуральні числа , які більше за 1, але не мають жодного простого дільника»
А – множина таких чисел;
А – найменше число із множини А, а ∈ А.
(а ∈ А) → (а>1, - а - найменше) → (а-просте) V (a - складене)
1 Випадок:
Число а – просте не може бути так як а ∈ А, а жодне число з цієї множини немає простих дільників, а тому саме не є просте.
2 Випадок:
Число а – складене, якщо так, то воно має натуральний дільник, нехай це буде число в, в ≠ 1, в ≠ а.
(а-складене) → (∃ в ∈ N, в-дільник, в ≠ 1, в ≠ а) → (а : в) → (в<a) → (в ∉ А)
а це протирічить тому що а - найменше числоу множині А, тому в ∉ А, звідси слідує
Якщо ( в ∉ А) → (∃ р - простий дільник в) → (в : р)
(а : в, в : р) → (а : р) – за властивістю транзитивності.
Цей факт, що а ділиться на р , означає , що а Є А , а це протирічить нашому припущенню;
Отже, наше припущення, що існують натуральні числа більше за 1 і які немають жодного простого дільника неправильне.
2, 3, 4, 5, 6, 7, 8, 9, 10
2 3 2 5 2; 3 3 2; 5
10.питання В теорії чисел основна теорема арифметики стверджує, що будь-яке натуральне число більше одиниці може бути представлене у вигляді добутку простих чисел і таке представлення є єдиним з точністю до порядку множників.
Пояснення. Для знаходження розкладу натурального числа на прості множники послідовно застосовується операція ділення числа на прості числа починаючи з найменшого. Причому, перехід до наступного більшого простого числа виконується тільки при неможливості цілого ділення на менше. Так, наприклад, можна отримати наступні розклади чисел 420 та 1200:
![]()
![]()
Таким чином, теоремою стверджується, що не існує таких чисел, які можна було б розкласти на прості множники різними способами.
Доведення.
Знаючи
розклад числа на прості множники, можна
отримати загальну кількість його
дільників. Будь-який додатний дільник
числа буде представлений тим же набором
простих чисел, але з меншими показниками
степеня у відповідних множників. Так,
наприклад, всі дотатні дільники числа
1200 будуть мати наступну форму ![]() де
де ![]() ,
, ![]() та
та ![]() .
Загальна кількість таких дільників
буде дорівнювати
.
Загальна кількість таких дільників
буде дорівнювати ![]() .
.
Розклад чисел на прості множники дає легкий спосіб визначення найбільшого спільного дільника та найменшого спільного кратного.
Узагальнення основної теореми арифметики на область цілих чисел дає можливість її представлення в алгебраїчних термінах[1], а саме: будь-який елемент, відмінний від нульового та одиничних, можна єдиним способом розкласти на прості множники з точністю до порядку множників та їхнього множення на одиничні елементи.
11) питання Нескінченність множини простих чисел (теорема Евкліда)
Множина простих чисел нескінченна. ► Доведемо теорему методом від супротивного. Припустимо, що множина простих чисел скінченна, тобто, що вона складається із простих чисел p1, p2, ..., pn. Розглянемо число g = p1·p2· ... ·pn + 1. Число g натуральне і більше одиниці, а тому воно має принаймні один простий дільник (теорема 21). Таким простим числом не може бути жодне з простих чисел p1, p2, ..., pn, бо число g при діленні на кожне з них дає в остачі 1. Отже, існує просте число, відмінне від чисел p1, p2, ..., pn. Значить, наше припущення про скінченність множини простих чисел хибне.
◄ Простим чи складеним є задане натуральне число, більше від 1, встановлюється на основі теореми, яка може бути використана як критерій простоти натурального числа. Теорема 23. Якщо натуральне число a більше одиниці не ділиться на жодне з простих чисел, квадрати яких не перевищують a, то число a просте.
► Доведемо теорему методом від супротивного. Припустимо, що число a складене. Тоді за властивістю простих чисел (наслідок 10) найменший його дільник, більший від 1, є числом простим. Позначимо його g. Матимемо a = g·a1, 1 < g < a, a1 > 1. За вибором числа g воно є найменшим дільником числа a, більшим від одиниці, і простим, а тому g £ a1. Звідси за монотонністю множення цілих невід'ємних чисел g2 £ a1·g, тобто g2 £ a. Отже, g є простим дільником числа a, квадрат якого не перевищує a, а це суперечить умові теореми.
◄ З теореми 23 одержується наслідок. Наслідок 11. Найменший простий дільник натурального числа не перевищує кореня квадратного з даного числа. Задача 3. Встановити, простим чи складеним є число 967.
► Для того, щоб
встановити простим чи складеним є число
967, потрібно на основі теореми 23
перевірити, чи є його дільниками всі
прості числа від 2 до 31, бо 312 = 961 < 967,
а 322 = 1024 > 967. За ознаками
подільності встановлюємо, що число 967
не ділиться на прості числа 2, 3, 5 і 11.
Безпосередньо перевіряємо, що це число
не ділиться на прості числа 7, 13, 17, 19, 23,
29 і 31. Отже, число 967 не ділиться на жодне
з простих чисел, квадрати яких не
перевищують числа 967, а тому воно буде
простим. Відповідь: число 967 – просте.
12
питання:

1 питання .Для довільних а та в на множині Z завжди можливі такі випадки :
1).(
будь-яке
a
 Z
нульове,будь-яке в
Z
нульове,будь-яке в
 N)
і
1(а:в)-націло —›(( а
N)
і
1(а:в)-націло —›(( а
 в)
–кратне)—›(а
в)
–кратне)—›(а в)<—>(
в)<—>( g
g
 Z
нульове,а=в
Z
нульове,а=в g)
g)
2).
(а не
 в)—›(
в)—›( (g,r)
(g,r) Zнульове),а=в
Zнульове),а=в g
g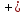 r,де
а
r,де
а r
r в)
в)
Властивості :
1) рефлексивне:
так як ( будь-яке а Z,a
Z,a a)
a)
2) антисиметричне:
так як ( а
а
 Z,
Z, в
в N,якщо
а
N,якщо
а
 в,то в
в,то в а)<—›(а=в)
а)<—›(а=в)
3) транзитивне:
так як (будь-яке а Z,
будь-яке в
Z,
будь-яке в N,
будь-яке с
N,
будь-яке с N)(
а
N)(
а в
в с)—>(а
с)—>(а с)
Теореми
про подільність суми і різниці:
с)
Теореми
про подільність суми і різниці:
Теорема 1(про подільність суми достатня умова)
Якщо кожен із доданків а1,а2,….,аn ділиться на деяке натуральне число в,то їх сума також поділиться на в.
Теорема2( про подільність суми необхідна і достатня умова)
Якщо один із двох доданків ділиться на число в, то щоб їх сума поділилась на в необхідно і достатньо,щоб і другий доданок поділився на в.
Теорема 3(про подільність різниці достатня умова)
Якщо зменшуване і від`ємник ділиться на число в ,то їх різниця ділиться на число в.
Теорема 4(про подільність різниці необхідна і достатня умова)
Різниця двох чисел ділиться на задане число тоді і тільки тоді коли остача цього діленого і від`ємник рівні між собою.
2. питання Теорема 1(про подільність суми достатня умова)
Якщо кожен із доданків а1,а2,….,аn ділиться на деяке натуральне число в,то їх сума також поділиться на в.
Доведення
За
у.т. (а1 в)—>(
в)—>( q1
q1
 N,а1
N,а1 в
в q1)
(1)
q1)
(1)
За
у.м. (а2 в)—>(
в)—>( q2
q2
 N,а2
N,а2 в
в
 q2)
(2)
q2)
(2)
(аn в)—>(
в)—>( q2n
q2n N,аn
N,аn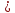 в
в
 qn)
(3)
qn)
(3)
Складемо таку суму
а1+а2+а3+а4+….аn в
в
 q1+
в
q1+
в q2+…..+в
q2+…..+в qn
= в(q1+q2+….+qn)=
в
qn
= в(q1+q2+….+qn)=
в q(a1+a2+….+an)=
в
q(a1+a2+….+an)=
в
 q,
q, q
q N)<—>(a1+a2+…..+an)
N)<—>(a1+a2+…..+an) в.
в.
Теорема2( про подільність суми необхідна і достатня умова)
Якщо один із двох доданків ділиться на число в, то щоб їх сума поділилась на в необхідно і достатньо,щоб і другий доданок поділився на в.
3. питання:Теорема 3(про подільність різниці достатня умова)
Якщо зменшуване і від`ємник ділиться на число в ,то їх різниця ділиться на число в.
Теорема 4(про подільність різниці необхідна і достатня умова)
Різниця двох чисел ділиться на задане число тоді і тільки тоді коли остача цього діленого і від`ємник рівні між собою.
Доведення
а1–а2=(в q1+r1)–(в
q1+r1)–(в q2+r2)=(в
q2+r2)=(в q1–
в
q1–
в
 q2)+(r1–r2)=в(q1–q2)+(r1
q2)+(r1–r2)=в(q1–q2)+(r1 r2)
r2)
(a1–a2) в)<—>(r1–r2)
в)<—>(r1–r2) в
в
Сума
представлена різниця , у якій згідно
Теоремою 2 необхідно і достатньо 2 доданки
r1–r2 в
в
Так
як 0≤r1≤в
і
0≤r2≤в,то
(r1–r2)<в—>(r1–r2=0,0 в)
в)
Якщо r1–r2=0, то r1=r2
19,20,21 питання Системи лінійних рівнянь з двома змінними розв’язуються одним із трьох способів:
1. Графічно — в одній системі координат будуються графіки двох рівнянь, і координати точки перетину графіків відповідають кореням рівнянь.
2. Способом підстановки — в одному рівнянні виражають перше невідоме через друге (або навпаки — друге через перше), а потім його значення підставляють у друге рівняння, дістаючи друге рівняння як рівняння з одним невідомим.
3. Способом алгебраїчного додавання — в обох рівняннях, використовуючи основні властивості рівнянь, урівнюються коефіцієнти при одному з невідомих так, що вони мають протилежні знаки (знаки «+> і«-») і однакові чисельно. Рівняння почленно додаються і сума коефіцієнтів при одному з невідомих перетворюється на нуль, тим самим перетворюючи на 0 весь одночлен.
Записавши нове рівняння (суму системи рівнянь), ми одержуємо лінійне рівняння з одним невідомим, розв’язуючи яке, знаходимо його корінь. Це числове значення невідомого підставляємо в будь-яке з двох рівнянь і обчислюємо числове значення другого невідомого.



25 питання Нерівністю з однією змінною називається нерівність, що містить одну незалежну змінну. Розв’язком нерівності називається будь-яке значення змінної, при якому початкова нерівність зі змінною обертається у правильну числову нерівність. Розв’язати нерівність зі змінною – значить знайти всі її розв’язки або довести, що розв’язків немає. Дві нерівності називаються рівносильними (еквівалентними), якщо розв’язки цих нерівностей збігаються; зокрема, нерівності рівносильні, якщо вони не мають розв’язків.
Основні теореми про рівносильні нерівності.
1. Якщо з однієї частини нерівності перенести до іншої доданок із протилежним знаком, то дістанемо нерівність, рівносильну початковій.
2. Якщо до обох частин нерівності додати (або відняти) будь-яке число, то дістанемо нерівність, рівносильну початковій.
3. Якщо обидві частини нерівності помножити (поділити) на додатне число, то дістанемо нерівність, рівносильну початковій; якщо обидві частини нерівності помножити (поділити) на від’ємне число, то рівносильною початковій буде нерівність протилежного змісту.
Лінійною нерівністю
з однією змінною називається нерівність
виду
![]() (або
(або![]() )
або така, яка зводиться до неї.
)
або така, яка зводиться до неї.
