Электростатика

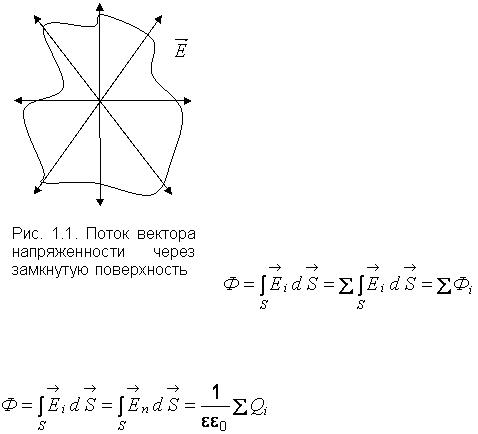
Электростатика. Применение теоремы Остроградского–Гаусса для расчета полей в вакууме

Закон Кулона позволяет рассчитать поле любой системы зарядов, т. е. найти его напряженность в любой точке, суммируя векторно напряженности, созданные отдельными зарядами (так как векторы напряженности подчиняются принципу суперпозиции). Напряженностью называют векторную физическую величину, характеризующую силу действия электростатического поля на положительный заряд. По направлению вектор напряженности совпадает с этой силой. Для задач, обладающих симметрией, вычисления можно значительно упростить; в этих случаях удобно воспользоваться теоремой Остроградского–Гаусса для потока вектора напряженности через некоторую замкнутую поверхность (рис. 1.1). Пусть все заряды Qi сосредоточены внутри замкнутой поверхности площадью S.

На элементе поверхности площадью dS заряды создают соответственно напряженности 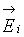причем полная

напряженность равна .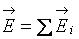

Поток Ф вектора напряженности 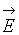через рассматриваемую замкнутую поверхность

.

Потоки векторов напряженности (скаляры) суммируются алгебраически. Учитывая значения Фi, можно переписать:

,

где 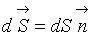( 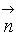– единичный вектор внешней нормали к элементу поверхности площадью dS); 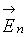– проекция вектор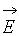а на 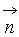; Qi – заряды, расположенные внутри поверхности.

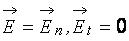
Теорема Остроградского–Гаусса формулируется следующим образом. Поток вектора 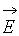через любую замкнутую поверхность пропорционален суммарному заряду, расположенному внутри этой поверхности.

Возможны три случая обращения в нуль потока вектора напряженности через замкнутую поверхность:

а) алгебраическая сумма зарядов внутри поверхности равна нулю, ;

б) зарядов внутри поверхности нет, но есть поле, связанное с внешними зарядами, 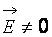; в) нет ни поля, ни внутренних зарядов.

Заряды могут быть распределены различным образом, причем они могут вноситься в рассматриваемое пространство, перемещаться в нем и изыматься из него, поэтому их называют свободными зарядами.

Если заряд dQ непрерывно распределен в некотором малом объеме dV. В этом случае вводится понятие объемной плотности заряда

ρ = dQ/dV (выражается в кулонах на кубический метр). Если заряды непрерывно распределены по поверхности проводника, то вводится понятие поверхностной плотности σ = dQ/dS, где dS – площадь элемента поверхности проводника, на котором расположен элементарный заряд dQ. Единицей поверхностной плотности является 1 Кл/м2. Если заряды равномерно распределены вдоль линии, в этом случае вводится понятие линейной плотности зарядов λ = dQ/dl, где dl – длина отрезка линии, на котором распределен заряд dQ. Единица линейной плотности – 1 Кл/м.

Вектор напряженности на поверхности заряженного проводника всегда перпендикулярен поверхности (например для заряженного шара, рис. 1.2), так как в противном случае заряды двигались бы вдоль поверхности под действием касательной составляющей напряженности. Таким образом, у поверхности проводника

,

а внутри сплошного проводника

.

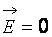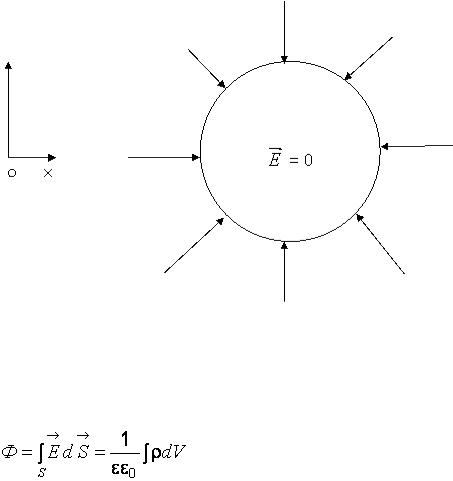
Рис. 1.2. Поле заряженного металлического шара

Если заряды распределены по объему диэлектрика с объемной плотностью ρ, то теорема Остроградского–Гаусса записывается в виде:

,

где dV – элемент объема; V – объем, ограниченный поверхностью S.

Когда заряды распределены по поверхности проводника, а поверхность интегрирования совпадает с последней, то

.

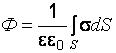Тогда на поверхности проводника напряженность пропорциональна поверхностной плотности заряда:

.

Поле положительного точечного заряда обладает сферической симметрией относительно точки, в которой он расположен, и характеризуется напряженностью, направленной по радиусам, проведенным из этой точки, и равной

т. е. подчиняется закону Кулона (для отрицательного заряда вектор направлен к этой точке). Таким же закономерностям подчиняется поле заряженного металлического шара. Заряд на шаре распределяется равномерно по поверхности. Тогда для металлического шара радиусомR0 напряженность поля определяется в соответствии с формулой (1.2).

Если внутри заряженного шара или другого металлического проводника имеется полость, в которую не внесены заряды, то поле внутри этой полости не может создаваться зарядами, находящимися на поверхности проводника. Так как поле внутри полости не связано ни с какими зарядами, то оно отсутствует, т. е. Епол = 0.

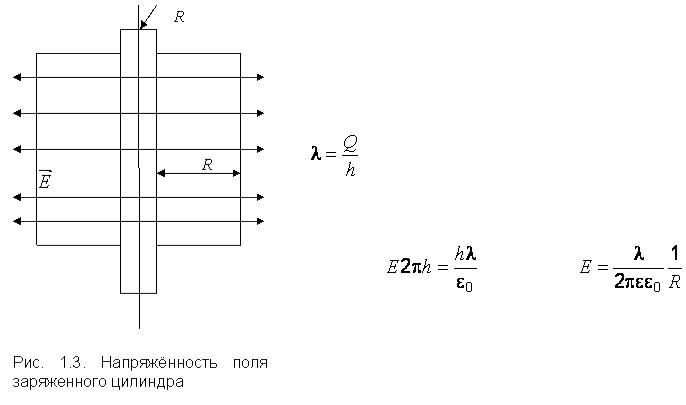
Практический интерес представляет поле, созданное длинной равномерно заряженной проволокой (цилиндром) радиусом R0 (рис. 1.3). Выбрав поверхность интегрирования в виде коаксиального цилиндра радиусом R и высотой h и введя линейную плотность заряда

убеждаемся, что в силу цилиндрической симметрии напряженность на боковой поверхности цилиндра везде одинакова по модулю и направлена по радиусам, а поток напряженности через основания отсутствует.

В этом случае напряженность поля меняется обратно пропорционально первой степени расстояния. На поверхности проволоки получаем

.

Найдем теперь напряженность поля безграничной плоской металлической пластины (рис. 1.4). Пусть пластина равномерно заряжена. В качестве поверхности интегрирования выберем поверхность

прямоугольного параллелепипеда, две грани которого площадью S параллельны заряженной пластине. Поверхностная плотность заряда равна

σ = Q/2S, так как пластина имеет две стороны и заряд распределен по обеим сторонам. Вследствие симметрии поток вектора напряженности для граней отличен от нуля. Следовательно,

. (1.3)

Для двух параллельных пластин (рис. 1.5), имеющих одинаковую по модулю плотность заряда, по принципу суперпозиций получим: а) для поля между пластинами

;

б) для поля снаружи пластин

.

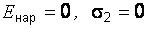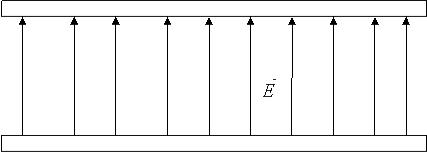
Рис. 1.5. Напряжённость поля двух параллельных пластин (плоского конденсатора)

Можно сделать вывод, что заряды собираются на обращенных друг к другу сторонах пластин с поверхностной плотностью σ1 = σ. Напряженность, определяемая выражением (1.3), не зависит от расстояния и одинакова во всех точках. Такие поля называют однородными. Реальных бесконечных проволок и пластин не бывает, но полученные формулы сохраняют значение для областей, достаточно близких к заряженным телам (расстояние до исследуемой точки поля должно быть много меньше линейного размера заряженного тела). Распределение линий напряженности можно получить на опыте, поместив электроды той или иной формы в жидкий диэлектрик (вазелиновое масло) и насыпав на поверхность масла мелкий диэлектрический порошок (хинин). Частицы порошка при этом располагаются примерно вдоль линий напряженности.

Теорему Остроградского–Гаусса можно использовать не только в интегральной форме, связывающей значения напряженности Е в некоторых точках поля с зарядами, расположенными в других точках, но и в дифференциальной форме. Свяжем величины, относящиеся к одной и той же точке поля.

Пусть в некоторой точке А с координатами (х, у, z) существует напряженность 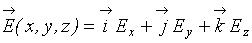где i, j, k – направляющие векторы в декартовой системе координат.

Выделим около точки А (рис. 1.6) прямоугольный параллелепипед бесконечно малого объема dV = dx`dy`dz.

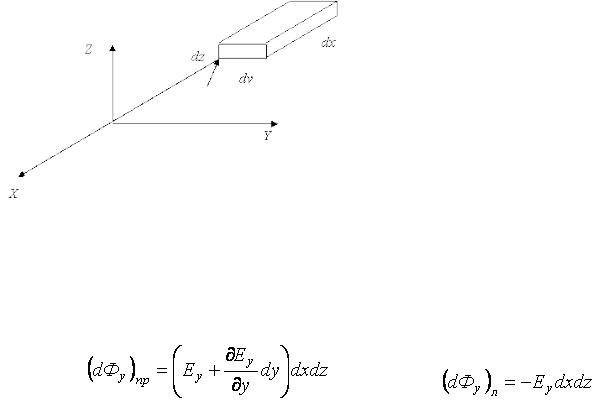
Рис. 1.6. К теореме Остроградского–Гаусса

Объемная плотность заряда в нем равна ρ. Она зависит от координат выбранной точки поля р = f (x, у, z). Поток вектора 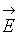через правую

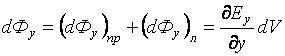. Таким же образом для верхней и нижней граней получим ,

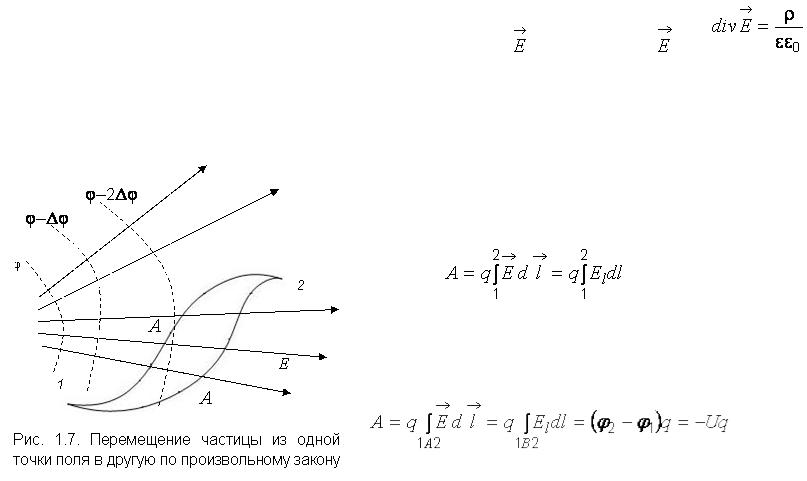
а для задней и передней граней 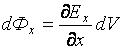. Применим теорему Остроградского–Гаусса к этому объему:

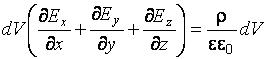,окончательно получим выражение 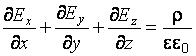. В векторном анализе сумма, стоящая

В этой форме теорема приложима к отдельным точкам поля.

Теорема Остроградского–Гаусса не является следствием закона Кулона. Она – одна из основных теорем векторного анализа, связывающая объемный интеграл с поверхностным. В физике эта теорема применяется к центральным силам, зависящим от расстояния по закону Rn, где n –любое число. Таким образом, кулоновский закон является частным случаем теоремы Остроградского–Гаусса.

Рассмотрим работу электростатических сил при перемещении частицы с зарядом q из одной Точки поля в другую по произвольному пути 1А2 (рис. 1.7):

где Ei – проекция вектора на направление dl. Эта работа будет зависеть только от положения начальной и конечной точек пути, а не от его формы, т. е. поле является потенциальным:

,

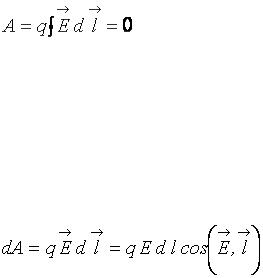
где φ1, φ2 – потенциалы начальной и конечной точек траектории. Потенциал является скалярной характеристикой точки поля. U = φ1 –φ2 – разность потенциалов или изменение потенциальной энергии единичного положительного заряда, переносимого в электростатическом поле.

Таким образом, работа электростатических сил пропорциональна разности потенциалов U начальной и конечной точек пути. Единицей потенциала и разности потенциалов является Вольт (В).

Работа электростатических сил по любому замкнутому пути равна нулю:

.

Этот интеграл называется циркуляцией вектора напряженности . Равенство нулю циркуляции означает, что в электростатическом поле нет замкнутых линий напряженности: они начинаются и кончаются на зарядах (соответственно положительных или отрицательных) или уходят в бесконечность.

В электростатическом поле можно построить (рис. 1.7) поверхности, представляющие собой множество точек равного потенциала (эквипотенциальные поверхности). Докажем, что линии напряженности нормальны к этим поверхностям. Если перемещать заряд вдоль эквипотенциальной поверхности, то работа будет равна нулю. Но напряженность поля на поверхности может быть отлична от нуля. Поэтому из определения элементарной работы

следует, что при 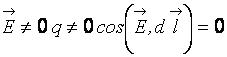, следовательно, , причем вектор dl направлен по касательной к поверхности.

Следовательно, во всех точках поверхности равного потенциала напряженность 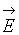направлена по нормали к этой поверхности. Из расчета полей симметричных проводников при помощи теоремы Остроградского–Гаусса видно, что поверхность проводника в электростатическом поле всегда эквипотенциальна.

Напряженность электростатического поля связана с потенциалом в каждой точке поля соотношением