Электростатика
.pdf
,(1.4)
где производная берется по нормали к эквипотенциальной поверхности, т. е. в направлении быстрейшего изменения потенциала. При этом положительная нормаль направлена в сторону увеличения потенциала, а вектор напряженности – в сторону его уменьшения. В соответствии с принципом суперпозиции потенциалы, создаваемые в данной точке различными зарядами, складываются алгебраически. Из (1.4) следует, что потенциал в каждой точке поля связан с напряженностью соотношением
,
где 
– единичный вектор; const – постоянная интегрирования. Это уравнение справедливо для любых электростатических полей.
На практике разность потенциалов измерять гораздо легче, чем напряженность поля, поэтому для описания поля потенциал применяется чаще. Рассмотрим потенциалы некоторых электростатических полей:
а) поле точечного заряда. Учитывая напряженность поля точечного заряда
,
получим потенциал
; (1.5)
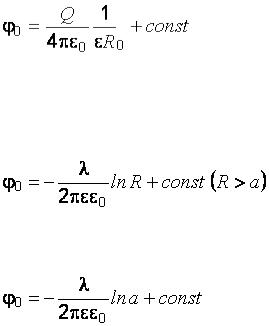
б) потенциал заряженного проводящего шара (радиусом R0). Так как внутри шара поле отсутствует, а вне шара описывается уравнением
(1.2),
то при R > R0 для потенциала справедливо уравнение (1.5); на поверхности шара (R = R0) получается
.
Это же значение потенциал имеет и внутри шара. В рассмотренных случаях произвольную постоянную удобно принять равной нулю, т. е. считать, что на бесконечности и потенциал, и напряженность обращаются в ноль; в) потенциал точек поля, созданного тонкой равномерно заряженной проволокой с линейной плотностью заряда λ:
.
На поверхности проволоки и внутри нее
.
Здесь нельзя считать потенциал бесконечно удаленных точек равным нулю, так как сама проволока считается бесконечно длинной. Поэтому постоянная остается неопределенной; но это не создает практических неудобств, потому что важно знать лишь разность потенциалов;
г) пусть бесконечная плоскость совпадает с координатной плоскостью YOZ и заряжена до поверхностной плотности σ/2. Поле вблизи плоскости однородно и Е = σ/2ε0. Поэтому потенциал является функцией только координаты х:
.
При х = 0 находим φ = С (потенциал пластины), причем снова постоянная интегрирования остается неопределенной. Если имеются две разноименно заряженные плоскости, параллельные друг другу, то заряды с плотностью ±σ скапливаются на обращенных друг к другу сторонах этих плоскостей и электростатическое поле существует только между плоскостями. Здесь можно принять за ноль потенциал одной из плоскостей, например координатной плоскости YOZ. Тогда получится:
Во многих практических случаях за ноль принимают потенциал земли и соединенных с нею проводников. Если окружить некоторую область заземленной проводящей замкнутой оболочкой, то потенциал оболочки также будет равен нулю; процессы внутри оболочки не будут зависеть от зарядов, находящихся вне ее (электростатическая защита).
При разделении зарядов приходится совершать некоторую работу, т. е. электростатическое поле (или система заряженных тел) должно обладать запасом энергии – электростатической энергией. Чтобы
оценить ее значение, вообразим две заряженные плоскости, расположенные бесконечно близко друг к другу. При поверхностной плотности зарядов ±σ поле между плоскостями имеет напряженность Е = σ/ε0.
Разведем плоскости на расстояние h. На заряд, находящийся на одной из плоскостей, действует поле заряда, находящегося на другой плоскости; напряженность этого поля равна Е1= Е/2 = σ/ε0 (так как сам на себя заряд не действует). Поэтому работа по перемещению заряда, сосредоточенного на поверхности площадью S, равна
.
Она определяет электростатическую энергию: A = W. Но энергию можно представить и так:
,
где Sh – объем части пространства, занятого полем.
В первом случае мы сосредоточиваем внимание на зарядах и приписываем им энергию, равную совершенной работе. Во втором случае мы сосредоточиваем внимание на поле и приписываем энергию каждому элементу объема поля. При этом плотность энергии поля
.
Это выражение справедливо и для неоднородных полей.
Найдем энергию поля, связанного с зарядом Q0, находящимся на проводящем шаре радиусом Ro, имеющем потенциал φ0. Ее можно назвать «собственной» энергией. Окружим шар концентрическим шаровым слоем (радиусы R и R+dR). Энергия поля в объеме этого слоя
,
а полная энергия поля
.
При переносе заряда Q0 из бесконечности (φ = 0) в точку поля с потенциалом φ0 совершается работа А = Q0φ0; она в 2 раза больше, чем в рассмотренном здесь случае. Это объясняется тем, что при постепенной зарядке шара отдельные элементарные заряды вносятся в постепенно возрастающее поле. Процесс зарядки таков: на незаряженный шар подается первый элементарный заряд dQ; при этом работа не совершается. Следующий заряд подается уже в поле первого заряда, что требует совершения некоторой работы, и т. д.
Если шар заряжен до потенциала φ, то работа сообщения шару дополнительного заряда dQ равна
, так как 
, где k–постоянный коэффициент пропорциональности.
Полная работа зарядки шара, равная энергии возникшего электростатического поля,
,
что соответствует ранее полученному результату.