ЗАМЕЧАНИЯ

Пересечение окружностей

Докажем, что две окружности могут либо не пересекаться, либо касаться в одной точке, либо пересекаться в двух точках, либо совпадать. Пусть окружност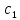и и 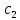имеют боле двух общих точек 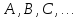. Точки 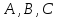не лежат на одной прямой (почему?), следовательно срединные перпендикуляры к отрезкам 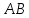и 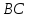пересекаются в одной точке О, равноудаленной от точек 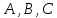. Так как срединный перпендикуляр к хорде проходит через центр окружности, то получаем, что точка О есть центр 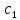и и 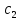. Так как радиусы этих окружностей совпадают с 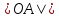, т.е. равны, то получаем .

Разложения триг функций в ряды

Разложение тригонометрических функций в ряды

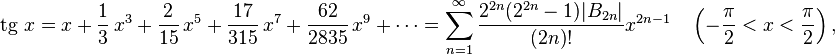
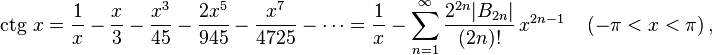
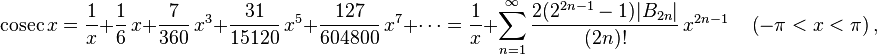
где

 — числа Бернулли,

 — числа Эйлера (англ. Euler numbers).

Числа Бернулли

Для чисел Бернулли существует следующая рекуррентная формула:

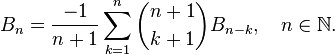г.

Все числа Бернулли с нечётными номерами, кроме , равны нулю, а знаки чисел Бернулли с чётными номерами чередуются.

Экспоненциальная производящая функция для чисел Бернулли: