
LEKTsII / Тема 19 КратныеКриволинейныеИнтегралы
.docxТема 19 «КРАТНЫЕ ИНТЕГРАЛЫ»
-
Двойной интеграл
Рассмотрим
на плоскости
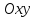 замкнутую область D, ограниченную линией
L. Пусть на области D задана функция
замкнутую область D, ограниченную линией
L. Пусть на области D задана функция
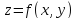 .
Разобьём область D на n частей
.
Разобьём область D на n частей
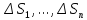 так, что все попарные пересечения
так, что все попарные пересечения
 не имеют внутренних точек (т.е. представляют
из себя кривую). Параметром
этого разбиения считаем наибольший
диаметр площадок
не имеют внутренних точек (т.е. представляют
из себя кривую). Параметром
этого разбиения считаем наибольший
диаметр площадок
 ;
при этом диаметром ограниченной замкнутой
площадки называется наибольшее из
расстояний между двумя точками этой
площадки. В каждой из площадок
;
при этом диаметром ограниченной замкнутой
площадки называется наибольшее из
расстояний между двумя точками этой
площадки. В каждой из площадок
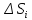 выберем точку
выберем точку
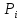 .
Составим интегральную сумму
.
Составим интегральную сумму
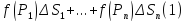
Если
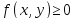 на области
на области
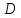 ,
то (1) -- сумма объёмов элементарных
цилиндров.
,
то (1) -- сумма объёмов элементарных
цилиндров.
Определение.
Предел интегральных сумм (1) при
→ 0 называется
двойным интегралом и обозначается
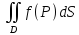 или
или
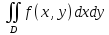 .
.
Если
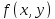 -- непрерывная функция, а граница области
-- непрерывная функция, а граница области
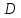 кусочно гладкая кривая, то двойной
интеграл существует.
кусочно гладкая кривая, то двойной
интеграл существует.
Геометрический
смысл двойного интеграла заключается
в том, что если
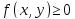 на области
на области
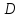 ,
то
,
то
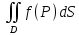 равен объёму тела
равен объёму тела
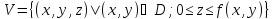
Свойства двойного интеграла
1. Двойной интеграл суммы двух функций равен сумме двойных интегралов.
2. Постоянный множитель можно выносить за знак двойного интеграла.
3.
(аддитивность) Если область D разбить
на две области
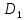 и
и
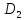 так, что пересечение
так, что пересечение
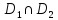 -- кривая, то
-- кривая, то
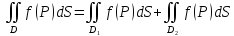 .
.
-
Вычисление двойного интеграла
Область
 на плоскости
на плоскости
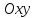 ,
которая может быть задана неравенствами
,
которая может быть задана неравенствами
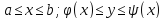
(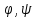 -- некоторые непрерывные функции с
условием
-- некоторые непрерывные функции с
условием
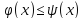 для любого
для любого
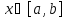 )
назовём правильной в направлении оси
)
назовём правильной в направлении оси
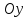 .
Аналогично определяется правильная
область в направлении оси
.
Аналогично определяется правильная
область в направлении оси
 .
.
Пусть
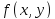 – функция, определенная на области D.
Выражение
– функция, определенная на области D.
Выражение
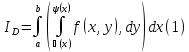
называется двукратным повторным интегралом и записывается часто как

Теорема. Двойной интеграл от непрерывной функции по правильной области равен двукратному интегралу.
Пример.
Вычислим интеграл
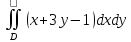 ,
где область
,
где область
 задана уравнениями граничных линий
задана уравнениями граничных линий
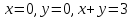 (имеется ввиду ограниченная часть
плоскости c указанными
граничными линиями). Область
(имеется ввиду ограниченная часть
плоскости c указанными
граничными линиями). Область
 правильная в направлении оси
правильная в направлении оси
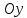 и может быть задана так
и может быть задана так
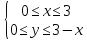
Тогда по теореме
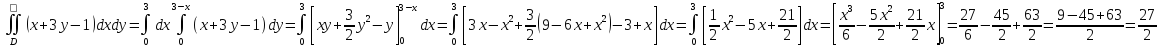
-
Двойной интеграл в полярных координатах.
Пусть
в полярной системе координат
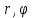 задана область
задана область
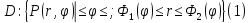
называемая
криволинейным сектором и на области D
задана непрерывная функция
 .
.
Дифференциал площади криволинейного сектора равен

Тогда
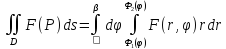
Пример. 1. Вычислим интеграл

2.
Вычислим интеграл Пуассона


Ответ:
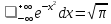
-
Тройной интеграл
Пусть
задана некоторая пространственная
область V. Разобьём её на области
 ,
так, что попарные пересечения
,
так, что попарные пересечения
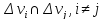 не имеют внутренних точек, и в каждой
области
не имеют внутренних точек, и в каждой
области
 возьмём точку
возьмём точку
 .
По-прежнему, через
.
По-прежнему, через
 обозначим наибольший диаметр областей
обозначим наибольший диаметр областей
 .
Пусть
.
Пусть
 -- функция, заданная на V. Тогда
-- функция, заданная на V. Тогда
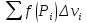 называется интегральной суммой, а
называется интегральной суммой, а

называется тройным интегралом. Достаточное условие существования тройного интеграла -- непрерывность функции f(P) и кусочная гладкость границы.
Пространственная
область V называется правильной в
направлении оси
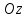 ,
если существуют числа
,
если существуют числа
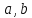 и функции
и функции
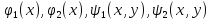 такие, что V состоит из всех точек
такие, что V состоит из всех точек
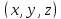 таких, что
таких, что
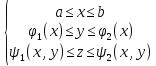
Для такой области имеет место равенство

-
Замена переменных в тройном интеграле
-
Тройной интеграл в цилиндрических координатах
-
Пусть
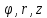 -- цилиндрические координаты. Разобьём
тело V поверхностями
-- цилиндрические координаты. Разобьём
тело V поверхностями
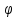 =Const,
=Const,
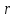 =Const, z =Const. Тогда дифференциал объёма
элементарного куска этого тела равен
=Const, z =Const. Тогда дифференциал объёма
элементарного куска этого тела равен
 .
Допустим, что тело V может
быть задано как:
.
Допустим, что тело V может
быть задано как:
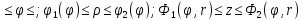
Тогда
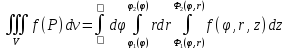
Пример.
Определить массу M полушара радиуса R с
центром в начале координат, если плотность
его вещества в каждой точке
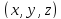 пропорциональна z, т.е. равна
пропорциональна z, т.е. равна
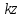 .
.
Имеем:
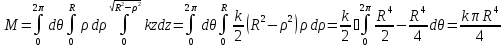
-
Тройной интеграл в сферических координатах
Пусть
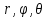 -- сферические координаты точки
-- сферические координаты точки
 .
Разобьём тело V поверхностями
θ =Const,
r=Const, 𝜑
=Const. Тогда объём
элементарного куска этого тела равен
.
Разобьём тело V поверхностями
θ =Const,
r=Const, 𝜑
=Const. Тогда объём
элементарного куска этого тела равен
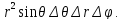
Тогда
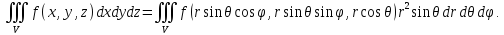
Пример. Найти объём шара радиуса R.
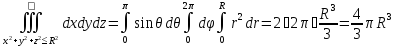
Криволинейные интегралы
-
Криволинейный интеграл по координатам
Имеется
кривая L в пространстве с началом M и
концом N и векторное поле F на L.
Разобьём L точками
 .
Обозначим
.
Обозначим
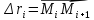 .
Параметром этого разбиения
назовём величину
.
Параметром этого разбиения
назовём величину
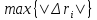 .
Составим интегральную сумму
.
Составим интегральную сумму
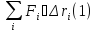
Криволинейным
интегралом поля F по
кривой L (обозначается
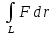 )
называется предел интегральных сумм
(1), если →
0.
)
называется предел интегральных сумм
(1), если →
0.
Замечание. Криволинейный интеграл -- работа силового поля F по перемещению материальной точки вдоль L.
Пусть
 и
и
 .
Тогда
.
Тогда
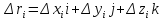
и

Поэтому

В
случае замкнутой кривой L, т.е. когда
M=N, криволинейный интеграл обозначают
 и
называют циркуляцией векторного поля
F по замкнутому контуру L.
и
называют циркуляцией векторного поля
F по замкнутому контуру L.
Достаточное
условие существования криволинейного
интеграла состоит в том, что
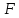 – непрерывное на кривой
– непрерывное на кривой
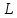 поле, а сама кривая
поле, а сама кривая
 кусочно-гладка
кусочно-гладка
Свойства криволинейного интеграла.
А. (линейность) Фиксируем кривую L. Тогда
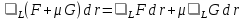
для любых векторных полей F,G и для любых чисел ,μ при условии, что интегралы в правой части существуют.
Б
(аддитивность). Пусть кривая L
равна сумме T+S
двух других кривых, и криволинейные
интегралы векторного поля F
по кривым T и S
существуют. Тогда, во-первых существует
интеграл
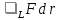 ,
а , во-вторых, имеет место равенство
,
а , во-вторых, имеет место равенство
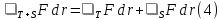
В.
(смена ориентации)

Г. (поле, ортогональное траектории) Предположим, что кривая L дифференцируема, и F⊥ dr/dt в любой точке кривой. Тогда криволинейный интеграл (3) равен 0.
Вычисление криволинейного интеграла. Если кривая L задана параметрически

причём
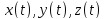 непрерывно дифференцируемы, а
непрерывно дифференцируемы, а
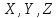 непрерывны,
то криволинейный интеграл существует
и равен определённому интегралу
непрерывны,
то криволинейный интеграл существует
и равен определённому интегралу

Пример
1. Криволинейный интеграл от
 вдоль
отрезка прямой [M(3,2,1), N(0,0,0)] равен -87/4.
вдоль
отрезка прямой [M(3,2,1), N(0,0,0)] равен -87/4.
Пример
2. Криволинейный интеграл от
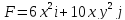 вдоль параболы
вдоль параболы
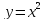 от точки M(1,1) до точки N(2,8) равен 3132.
от точки M(1,1) до точки N(2,8) равен 3132.
-
Площадь плоской области, ограниченной замкнутой кривой
Следствие формулы Грина (см. ниже) есть

Пример.
Вычислим площадь эллипса x=acos
t,y=bsin
t. Ответ--
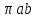 .
.
-
Вычисление работы силы
Пример Вычислить работу силы тяжести при перемещении некоторого груза.
-
Формула Грина
Пусть
D -- правильная область в направлении
оси
 ,
ограниченная кривой L. Тогда легко
вычислить
,
ограниченная кривой L. Тогда легко
вычислить

Аналогично,
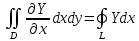
(знак
минус объясняется изменением ориентации
плоскости при замене
 на
на
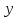 и наоборот – это есть отражение
относительно бисектриссы
и наоборот – это есть отражение
относительно бисектриссы
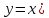
Отсюда получаем формулу Грина
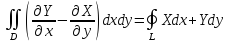
-
Независимость криволинейного интеграла от пути интегрирования
Во-первых - криволинейный интеграл не зависит от пути интегрирования тогда и только тогда когда по любому замкнутому контуру он равен 0.
Теорема.
Пусть граница
 состоит из одной непрерывной кусочно-гладкой
линии, а
состоит из одной непрерывной кусочно-гладкой
линии, а
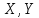 непрерывны вместе со своими частными
производными. Тогда циркуляция по любому
замкнутому контуру равна 0 тогда и только
тогда когда выполняется условие
непрерывны вместе со своими частными
производными. Тогда циркуляция по любому
замкнутому контуру равна 0 тогда и только
тогда когда выполняется условие
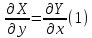
во всех точках области.
Если
это так, то существует потенциал
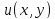 поля F, т.е. такая функция, что
поля F, т.е. такая функция, что
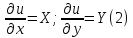
и тогда
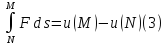
вне зависимости от пути, соединяющего точки M и N.
В условиях теоремы формула для вычисления потенциала следующая:

Если
точку
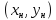 соединить с точкой
соединить с точкой
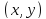 ломаной идущей от
ломаной идущей от
 до
до
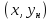 а затем до
а затем до
 ,
то предыдущая формула конкретизируется
так:
,
то предыдущая формула конкретизируется
так:

