Разложение элементарных функций по формуле Маклорена
Разложение экспоненты
Для
всех x∈ℝимеет место разложение

где

Например,
если
 ,
то
,
то

Тем
самым
 cточностью
cточностью
Разложение синуса и косинуса
Для
всех
 имеет место разложение
имеет место разложение

где

Для
всех
 имеет место разложение
имеет место разложение

где

Бином Ньютона
Для
каждого действительного числа α и для
каждого
 определим биномиальный коэффициент
определим биномиальный коэффициент

По
определению полагаем также, что
 .
Имеем:
.
Имеем:

Теорема.
Для любого действительного α и для
любого имеет место разложение
имеет место разложение

причем
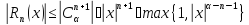
Рассмотрим
частные случаи формулы (5).
Случай
α =m -- натуральное число. Тогда
 и мы получаем бином Ньютона
и мы получаем бином Ньютона

Случай
 .
Тогда нетрудно вывести, что
.
Тогда нетрудно вывести, что .
Поэтому
.
Поэтому

где

Разложение логарифма
Из
(8) или непосредственно нетрудно получить

где

20




 ,
то
,
то
 cточностью
cточностью
 имеет место разложение
имеет место разложение

 имеет место разложение
имеет место разложение

 определим биномиальный коэффициент
определим биномиальный коэффициент
 .
Имеем:
.
Имеем:
 имеет место разложение
имеет место разложение
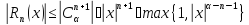
 и мы получаем бином Ньютона
и мы получаем бином Ньютона
 .
Тогда нетрудно вывести, что
.
Тогда нетрудно вывести, что .
Поэтому
.
Поэтому


