5. Правило Лопиталя

Теорема. Пусть функциидифференцируемы в окрестности точкии. Предположим также, чтов некоторой достаточно малой проколотой окрестности точки. Если существует предел отношения производныхпри, то существует предел отношения функций, и эти два предела совпадают:

Доказательство. Имеем

Здесь мы применили теорему Коши к отрезку и нашли точку.□

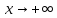Правило Лопиталя для бесконечности. Пусть функциидифференцируемы для всех достаточно больших. Предположим также, чтодля всех достаточно больших. Еслии существует предел отношения производныхпри, то существует предел отношения функций и эти два предела совпадают:

Аналогичный результат имеет место и для -∞ .

Замена t=1/x сводит доказательство к случаю a=0 правила Лопиталя.

Правило Лопиталя для неопределенности ∞/∞ .Пусть функциидифференцируемы для всех достаточно больших. Предположим также, чтодля всех достаточно больших x. Еслии существует предел отношения производныхпри x→+∞ , то существует предел отношения функций и эти два предела совпадают (см (2)).

Аналогичный результат имеет место и для -∞ .

Замена дроби f/g на (1/g)/(1/f) сводит доказательство к предыдущему случаю.

Пример.

1. Сравнение степени возрастания показательных, степенных и логарифмических функций.

Для любого и для любого натурального n имеет место соотношение

а также соотношение

Для доказательства этих соотношений следует применить правило Лопиталя достаточно количество раз. Эти соотношения обобщаются на случай, когда -- любое действительное число.

Пример.

6. Формула Тейлора

Ставится задача приблизить (аппроксимировать) функцию в окрестности точкимногочленом степени n. Для n=1 мы уже нашли решение: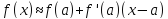. Удобно точкой отсчета считать нулевую точку, т.е. от координатмы переходим к приращениями. Ряд

представляется из себя семейство бесконечно малых величин, каждая последующая из которых есть б.м. большего порядка, чем предыдущая. Поставим задачу о разложении вида

где остаточный член есть б.м. высшего порядка по сравнению с. Деля (1) наи устремляяполучаем. Найдем другие коэффициенты в этом разложении:

Локальная формула Тейлора. Пусть функциядифференцируема в окрестности точкиn раз, и n-ая производная непрерывна в точке. Тогда

Доказательство. Применяем n раз правило Лопиталя к вычислению предела отношения

и доказываем, что этот предел равен 0.□

В условиях теоремы функция раскладывается в окрестности точки a в сумму многочлена степени ≤ n от переменнойи остаточного члена, про который известно, что он есть величина бесконечно малая высшего порядка по сравнению с.

Функция линейна по переменной, она называется дифференциаломв точкеи обозначаетсяЛегко видеть, что. Мы получаем «симметричный» вид дифференциала вычисленный в произвольной точке:

Отсюда получаем, что производная равна отношению дифференциалов:

Аналогично, функция называется дифференциалом -го порядка и обозначается. Ее симметричный вид есть. Тогда локальная формула Тейлора в дифференциалах принимает вид:

Уточним вид остаточного члена

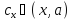Формула Тейлора с остаточным членом в форме Лагранжа. Пусть функциядифференцируема в окрестности точкиn+1 раз. Тогда для всехдостаточно близких кнайдется точкатакая, что

В частности, если , то имеет место следующая оценка остаточного члена:

Частный случай формулы Тейлора -- формула Маклорена получается при . Тогда при наличии n+1 производной в окрестности нуля, для каждого достаточно малогонайдетсятакой, что