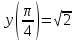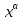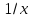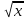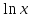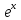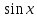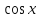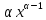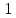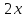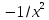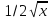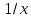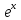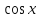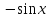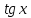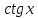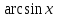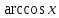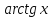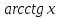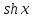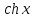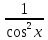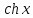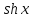2. Основные правила дифференцирования.

Д1. Производная константной функции равна нулю: (C)'=0.

Д2. Производная суммы равна сумме производных:.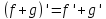

Д3. Постоянный множитель можно выносить за знак производной:.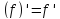

Д4. (правило Лейбница—производная произведения).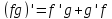

Доказательство.

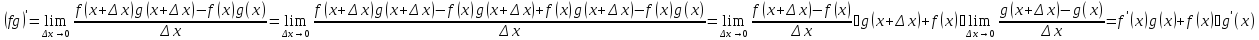
Здесь мы применили правила предел суммы и предел произведения, а также заменили 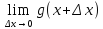нав виду непрерывности функции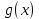(см. предложение выше)

Д5.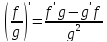; в частности.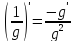

Докажем утверждение «в частности».

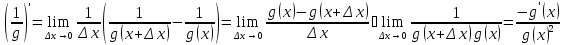
Общий случай следует из этого частного случая в виду правила Лейбница

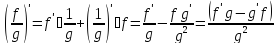
Д6. (производная сложной функции)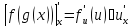

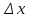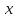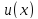Обоснуем эту формулу. Придадим приращение переменной. Тогдаполучит приращение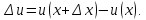Следовательно,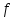получит приращениеДалее:

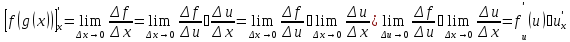
Заме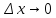на на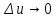возможна в силу непрерывности дифференцируемой функции.

Д7. ( производная обратной функции}) Пусть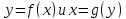-- две взаимно обратные функции. Тогда.

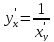Действительно, из 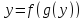дифференцированием по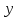следует соотношение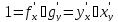, откуда получаем результат.

1. Таблица производных

Функция
Производная

Функция
Производная

Здесь 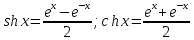-- гиперболические синус и косинус соответственно. Обоснуем формулу производной синуса:

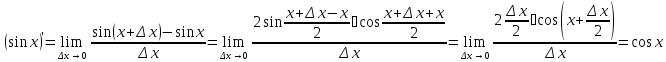
Здесь мы воспользовались эквивалентностью 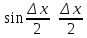а также непрерывностью функции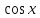.Вычислим производную косинуса:

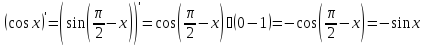
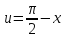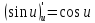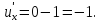Здесь мы воспользовались формулой производная сложной функции, введя промежуточный аргумент и учитывая, аПроизводная тангенса:

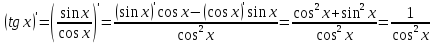
Производная экспоненты:

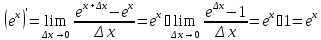
Производная логарифма считается с применением правила «производная обратной функции»

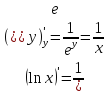
3. Другие приемы дифференцирования

1. Неявно заданные функции.

Пусть для уравнения

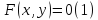
и отрезков верно следующее: для любогонайдется единственное значение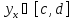(зависящее от x) такое, что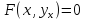. Тогда получаем закон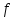в силу которого любому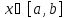ставится в соответствие число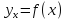такое, что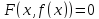. В этом случае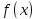-- функция, заданная неявно уравнением (1) в прямоугольнике.

Пример.Соотнoшение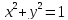в области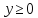задает функцию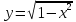, а в области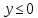-- функцию.

Метод дифференцирования неявно заданных функций.

1. Дифференцируем (1) по 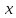, считая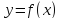функцией аргумента x.

2. Из полученного соотношения выражаем 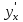через y и x. Пусть результат будет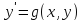

3. Если даны координаты 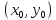такие, ч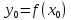то, то.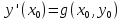

Пример. Найдем производную функции, заданной неявно соотношением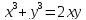в окрестности точки. Дифференцируем данное отношение по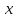, получим: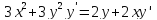. Отсюда находим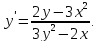В точке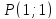эта производная равна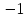и уравнение касательной будет иметь вид

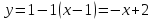
2. Параметрически заданные функции

Пусть

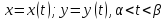
-- кривая на плоскости, заданная параметрически. Предположим, что для любого 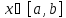найдется единственное значение параметра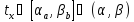такое, что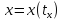. Тогда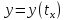называется функцией, заданной параметрически.

Пример. Соотношения

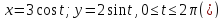
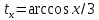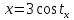задают эллипс с полуосями 3 и 2. Для любого x∈[0,3] найдется единственное число, а именнотакое, что. Тогда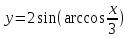-- функция, заданная параметрически соотношением (*), и которую в данном случае мы записали как элементарную функцию (другая запись той же функции --).

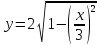Имеет место следующая формула, для производной функции, заданной параметрически:

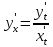
Действительно, дифференцируя 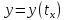по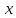как сложную функцию с промежуточным аргументом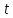, получаемНо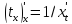согласно правила дифференцирования обратной функции. Подставляя, получим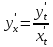, что и требовалось доказать.□

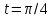Пример. Найдем касательную к эллипсу при. Значения функций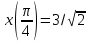;