
- •Оглавление
- •Определение производной
- •Основные правила дифференцирования.
- •Другие приемы дифференцирования
- •Неявно заданные функции.
- •Параметрически заданные функции
- •Логарифмическая производная
- •Теорема Лагранжа
- •Минимумы и максимумы
- •Правило Лопиталя
- •Сравнение степени возрастания показательных, степенных и логарифмических функций.
- •Формула Тейлора
- •Разложение элементарных функций по формуле Маклорена
Производная
Оглавление
1Определение производной 1
2Основные правила дифференцирования. 5
2.1 Таблица производных 6
3Другие приемы дифференцирования 8
3.1Неявно заданные функции. 8
3.2Параметрически заданные функции 9
3.3Логарифмическая производная 10
4Теорема Лагранжа 11
4.1Минимумы и максимумы 11
5Правило Лопиталя 14
5.1Сравнение степени возрастания показательных, степенных и логарифмических функций. 15
6Формула Тейлора 15
7Разложение элементарных функций по формуле Маклорена 18
7.1Разложение экспоненты 18
7.2Разложение синуса и косинуса 18
7.3Бином Ньютона 19
7.4Разложение логарифма 20
Определение производной
Задача
о мгновенной скорости. Рассмотрим
материальное тело движущееся по оси
Ох. Предположим, что нам известен закон
движения – функция ,
задающая координату точки в момент
времени
,
задающая координату точки в момент
времени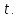 Фиксируем какой-либо момент времени
Фиксируем какой-либо момент времени .
Поставим задачу об определении и
вычислении мгновенной скорости
.
Поставим задачу об определении и
вычислении мгновенной скорости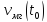 в момент времени
в момент времени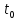 .
Придадим приращение
.
Придадим приращение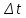 времени и найдем соответствующее ему
приращение координаты
времени и найдем соответствующее ему
приращение координаты . Тогда отношение приращения координаты
к приращению времени задает среднюю
скорость на временном участке
. Тогда отношение приращения координаты
к приращению времени задает среднюю
скорость на временном участке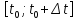 :
:
 (1)
(1)
Мгновенную
скорость определим как предел средней
скорости при
 :
:

Пример.Закон падения тела с высоты без учета
сопротивления воздуха задается как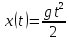 (
(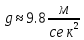 -- ускорение свободного падения). Вычислим
скорость тела после 3-х секунд падения:
-- ускорение свободного падения). Вычислим
скорость тела после 3-х секунд падения:

Задача о касательной. Пусть на
плоскости или в пространстве задана
некоторая кривая γ и точка P на ней.
Требуется определить понятие касательной
к γ в точке P. Выберем точку на кривой
на кривой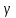 ,
не совпадающую с точкой
,
не совпадающую с точкой .
Проведем через точки
.
Проведем через точки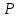 и
и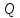 прямую
прямую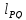 ,
называемую секущей.Касательной в
точке P к кривой γназовем предельное
положение секущих
,
называемую секущей.Касательной в
точке P к кривой γназовем предельное
положение секущих ,
в случае, когда точка Q приближается к
точке P, оставаясь на кривой γ. Пусть
теперь γ -- график функции
,
в случае, когда точка Q приближается к
точке P, оставаясь на кривой γ. Пусть
теперь γ -- график функции ,
и точка P имеет координаты
,
и точка P имеет координаты .
Рассмотрим точку
.
Рассмотрим точку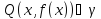 . Обозначим
. Обозначим и назовем эти величины приращением
аргумента и приращением функции
соответственно. Тогда угловой коэффициент
секущей
и назовем эти величины приращением
аргумента и приращением функции
соответственно. Тогда угловой коэффициент
секущей будет равен
будет равен и ее уравнение будет
и ее уравнение будет
Рис. 1 Касательная

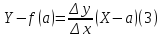
Если
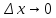 ,
то
,
то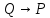 ,
причем
,
причем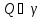 и секущая (3) переходит в касательную с
угловым коэффициентом
и секущая (3) переходит в касательную с
угловым коэффициентом

Пример.
Найдем касательную к кубической
параболе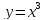 в точке
в точке .
Имеем
.
Имеем

Отсюда
получаем ответ:
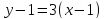 или
или . Это и есть уравнение искомой касательной.
. Это и есть уравнение искомой касательной.
Определение.Предел
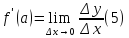
называется
производной функции
 в точке
в точке .
.
Функция
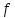 называется дифференцируемой на интервале,
если она имеет производную в каждой
точке этого интервала.
называется дифференцируемой на интервале,
если она имеет производную в каждой
точке этого интервала.
Можно
определить правую производную в точке
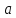 ,
рассматривая в (5) правый предел
,
рассматривая в (5) правый предел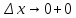 .
Такая производная обозначается
.
Такая производная обозначается .
Аналогично определяется левая производная
.
Аналогично определяется левая производная Производная
Производная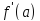 существует тогда и только тогда существуют
и совпадают между собой односторонние
производные. Односторонние производные
удобно использовать, когда мы говорим
о дифференцируемости функции
существует тогда и только тогда существуют
и совпадают между собой односторонние
производные. Односторонние производные
удобно использовать, когда мы говорим
о дифференцируемости функции на отрезке
на отрезке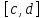 .
Тогда подразумевается, что
.
Тогда подразумевается, что имеет (двустороннюю) производную в
каждой внутренней точке
имеет (двустороннюю) производную в
каждой внутренней точке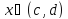 ,
а также имеет односторонние производные
,
а также имеет односторонние производные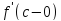 и
и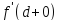 .
.
Итак:
механический смысл производной --
мгновенная скорость. Геометрический
смысл производной -- тангенс угла наклона
касательной к графику функции в точке
в точке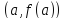 .
.
Уравнение
касательной к графику функции
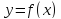 в
точке
в
точке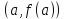 имеет вид:
имеет вид:
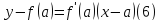
а уравнение нормали имеет вид:
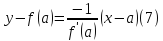
в
предположении
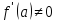 .
Если же
.
Если же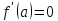 ,
то касательная горизонтальна и задается
уравнением
,
то касательная горизонтальна и задается
уравнением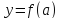 ,
а нормаль перпендикулярна оси Ох и
задается уравнением
,
а нормаль перпендикулярна оси Ох и
задается уравнением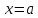 .
.
Примеры.1.
2.
 .
Действительно,
.
Действительно,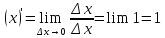
3.
 .
Действительно,
.
Действительно,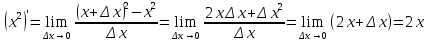
4.
Функция
 в нуле непрерывна, но не имеет производной.
Правая производная в нуле равна 1, а
левая равна
в нуле непрерывна, но не имеет производной.
Правая производная в нуле равна 1, а
левая равна .
.
Предложение 1. Дифференцируемая функция непрерывна.
Действительно,
из соотношения
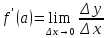 вытекает, что
вытекает, что отличается от
отличается от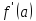 на бесконечно малую величину
на бесконечно малую величину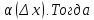
 и
и
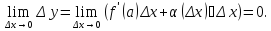
Это
и означает непрерывность функции
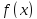 в точке
в точке .□
.□
Заметим,
что непрерывная функция не обязательно
будет дифференцируемой, см. выше пример
функции
 в точке
в точке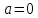 .
.
