Схемотехнические методы

Эти методы основаны на построении электрических, магнитных или электромагнитных схем замещения моделируемого объекта и последующем анализе режимов и процессов методами теории цепей. Если схема замещения достаточно сложная, то при анализе применяются топологические соотношения в матричной форме.

Схемотехнические методы моделирования электрофизических процессов достаточно подробно рассмотрены в дисциплине «Теоретические основы электротехники» (теория цепей).

Отметим только, что топологические соотношения могут быть использованы и для анализа режимов нелинейных цепей экономичными методами: узловых потенциалов, контурных токов, напряжений ветвей дерева.

Если это метод узловых потенциалов, то нелинейное матричное уравнение состояния цепи имеет вид

(1)

где нелинейная функция f в левой части уравнения (1) вычисляет алгебраические суммы токов ветвей, присоединённых к не общим узлам по задаваемым значениям узловых потенциалов. В результате выполнения итерационной процедуры определяются узловые потенциалы, удовлетворяющие уравнению (1) с некоторой заданной точностью сходимости. Если столбец вольт- амперных характеристик пассивных участков ветвей обозначить то определяющее матричное выражение для функции f, входящей в (1), имеет вид

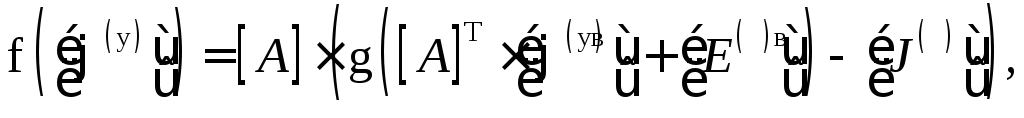
где [A] – матрица узловых соединений; – столбец узловых потенциалов;– столбец ЭДС ветвей;– столбец источников тока ветвей.

Нелинейное матричное уравнение состояния цепи в методе напряжений ветвей дерева имеет вид

(2)

где нелинейная функция f в левой части уравнения (2) вычисляет алгебраические суммы токов ветвей, принадлежащих главным сечениям цепи по задаваемым значениям напряжений ветвей дерева. Определяющее матричное выражение для функции f, входящей в (2), имеет вид

где [Q] – матрица главных сечений; – столбец напряжений ветвей дерева.

Нелинейное матричное уравнение состояния цепи в методе контурных токов имеет вид

(3)

где нелинейная функция f в левой части уравнения (3) вычисляет алгебраические суммы напряжений ветвей, принадлежащих главным контурам цепи по задаваемым значениям контурных токов (токов ветвей связи). Если столбец вольт- амперных характеристик пассивных участков ветвей обозначить то определяющее матричное выражение для функции f, входящей в (3), имеет вид

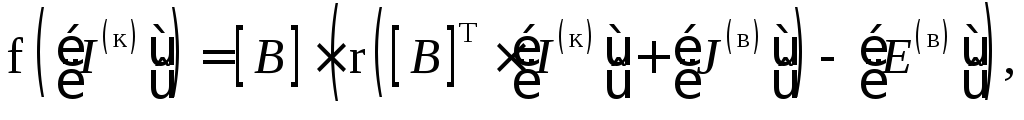
где [B] – матрица главных контуров; – столбец токов ветвей связи.

Уравнения (1), (2), (3) пригодны для моделирования статических режимов работы нелинейных электрических и магнитных цепей, т.е. таких установившихся режимов, когда ЭДС и токи источников либо не изменяются во времени, либо для любого момента времени текущее состояние цепи определяется только мгновенными значениями ЭДС и токов источников и не зависит от временных производных и первообразных этих величин. Статические режимы при переменных ЭДС и токах источников возможны только тогда, когда пассивные элементы цепи обладают чисто резистивными свойствами.

Если электрическая схема замещения содержит индуктивные и ёмкостные элементы, то процессы в таких цепях описываются не алгебраическими, а дифференциальными уравнениями (ДУ). Если моделируемая цепь с сосредоточенными параметрами, то процессы в ней описываются обыкновенными дифференциальными уравнениями (ODE). Для решения ODE существуют стандартные решатели (например, в системе MATLAB), реализующие численные методы. Наиболее корректно эти решатели подключаются, если система ODE цепи сформирована методом переменных состояния. В качестве переменных состояния лучше всего выбирать магнитные потокосцепления идеальных индуктивных элементов и заряды идеальных ёмкостных элементов. Первые производные по времени от этих физических величин представляют собой напряжения на зажимах индуктивностей и токи в ёмкостях. В соответствии со сказанным, система уравнений электрической цепи с сосредоточенными параметрами в пространстве состояний имеет вид

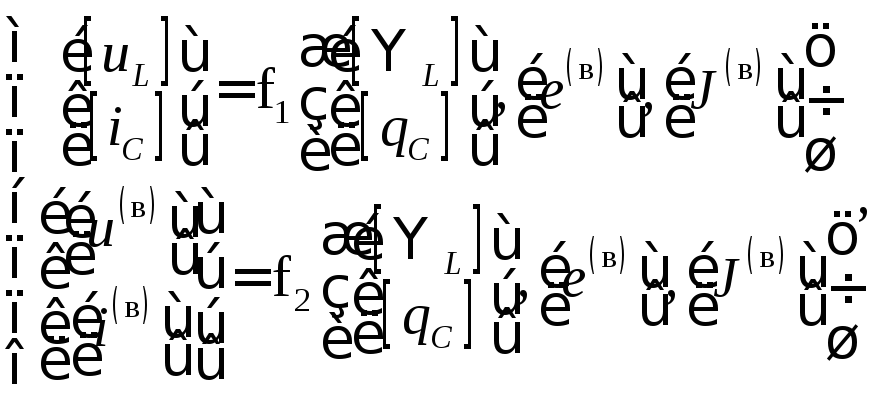(4)

где [u_L] – столбец мгновенных напряжений на зажимах идеальных индуктивных элементов; [i_C] – столбец мгновенных токов в идеальных ёмкостных элементах; f₁ – нелинейная функция передач от переменных состояния и мгновенных параметров источников к скоростям изменения переменных состояния; – столбец мгновенных потокосцеплений в идеальных нелинейных индуктивностях;– столбец мгновенных зарядов в идеальных нелинейных ёмкостях;– столбец мгновенных значений переменных состояния моделируемой цепи;– столбец мгновенных значений ЭДС ветвей;– столбец мгновенных значений токов источников ветвей;– столбец мгновенных значений напряжений ветвей;– столбец мгновенных значений токов ветвей;f₂ – нелинейная функция передач от переменных состояния и мгновенных параметров источников к напряжениям и токам ветвей.

Пусть схема замещения цепи состоит из нелинейных идеализированных двухполюсников: резистивных, индуктивных и ёмкостных, а также идеальных источников ЭДС и тока. Чтобы построить удобный способ матричного представления нелинейных функций f₁ и f₂, входящих в уравнения (4), нужно при описании топологии цепи каждый двухполюсник считать отдельной ветвью, причём все источники ЭДС и ёмкостные элементы должны являться ветвями дерева, т.к. напряжения на зажимах источников ЭДС всегда известны, а напряжения на зажимах емкостных элементов функционально (кулон- вольтными характеристиками) связаны с зарядами, которые являются входными аргументами нелинейных функций f₁ и f₂. Все источники тока и индуктивные элементы должны являться ветвями связи, т.к. токи источников тока всегда известны, а токи индуктивных элементов функционально (вебер- амперными характеристиками) связаны с магнитными потокосцеплениями, которые являются входными аргументами нелинейных функций f₁ и f₂. Резистивные элементы могут быть как ветвями дерева, так и ветвями связи.

В связи с изложенными соображениями все ветви схемы замещения нужно разделять на 6 групп: 1) ветви дерева с идеальными источниками ЭДС, 2) ветви дерева с идеальными ёмкостями, 3) резистивные ветви дерева, 4) резистивные ветви связи, 5) ветви связи с идеальными индуктивностями, 6) ветви связи с идеальными источниками тока. Наиболее удобным компьютерным представлением топологии цепи является матрица узловых соединений [A], которую можно представить в виде горизонтальной склейки двух блоков: 1) узловая матрица ветвей дерева [A_д], 2) узловая матрица ветвей связи [A_к]. Для вывода определяющих матричных выражений функций f₁ и f₂ наиболее удобна матрица главных сечений [Q], которая может быть получена из матрицы [A].

где [Q_д]=[1_д] – блок матрицы [Q], соответствующий только ветвям дерева, [1_д] – единичная матрица размера (д,д), где д – число ветвей дерева; [Q_к] – блок матрицы [Q], соответствующий только ветвям связи; [B_д] – блок матрицы [B], соответствующий только ветвям дерева, [B_к]=[1_к] – блок матрицы [B], соответствующий только ветвям связи, [1_к] – единичная матрица размера (к,к), где к – число ветвей связи. Последние соотношения показывают, что для записи обоих законов Кирхгофа достаточна только одна матрица [Q_к]. С помощью этой матрицы выразим по первому закону Кирхгофа токи ветвей дерева через токи ветвей связи и по второму закону Кирхгофа выразим напряжения ветвей связи через напряжения ветвей дерева:

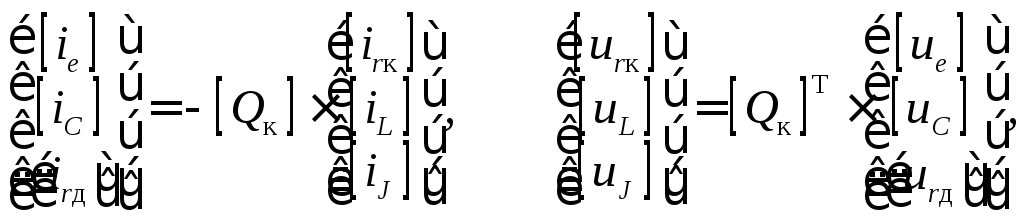(5)

где [i_e] – матрица- столбец токов, протекающих через источники ЭДС; [i_C] – матрица- столбец токов, протекающих через идеальные ёмкости; [i_rд] матрица- столбец токов, протекающих через резистивные ветви дерева; [i_rк] – матрица- столбец токов, протекающих через резистивные ветви связи; [i_L] – матрица- столбец токов, протекающих через идеальные индуктивности; [i_J] – матрица- столбец токов, протекающих через идеальные источники тока; [u_rк] – матрица- столбец напряжений на резистивных ветвях связи; [u_L] – матрица- столбец напряжений на идеальных индуктивностях; [u_J] – матрица- столбец напряжений на идеальных источниках тока; [u_e] – матрица- столбец напряжений на идеальных источниках ЭДС; [u_C] – матрица- столбец напряжений на идеальных ёмкостях; [u_rд] – матрица- столбец напряжений на резистивных ветвях дерева. В общем случае взаимосвязи между величинами [i_L] и , [u_C] и [q_C], [i_rк] и [u_rк], [i_rд] и [u_rд] являются нелинейными. Именно эти нелинейности обуславливают нелинейный характер функций f₁, f₂, входящих в уравнения (4). Далее рассмотрим случай, когда эти взаимосвязи линейные:

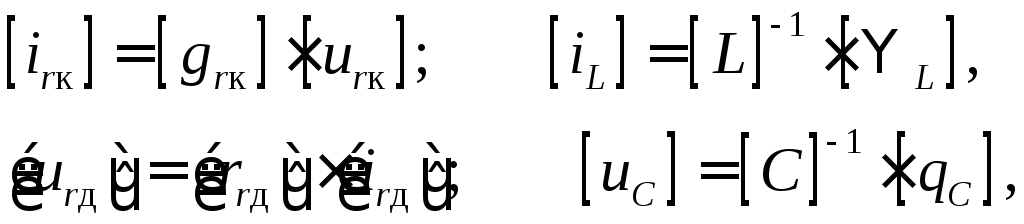(6)

где [g_rк] – матрица проводимостей резистивных ветвей связи (в простейшем случае диагональная); [L] – матрица индуктивностей ветвей; [r_rд] – матрица сопротивлений резистивных ветвей дерева; [C] – матрица ёмкостей ветвей.

Чтобы развернуть блочно- матричные соотношения (5), матрицу [Q_к] представим склейкой блоков:

где [Q_rк] – блок матрицы [Q_к], соответствующий только резистивным ветвям связи; [Q_L] – блок матрицы [Q_к], соответствующий только индуктивным ветвям; [Q_J] – блок матрицы [Q_к], соответствующий только ветвям с идеальными источниками тока; [Q_rк,e] – блок матрицы [Q_rк], соответствующий главным сечениям, образованным источниками ЭДС; [Q_rк,C] – блок матрицы [Q_rк], соответствующий главным сечениям, образованным ёмкостными ветвями; [Q_rк,rд] – блок матрицы [Q_rк], соответствующий главным сечениям, образованным резистивными ветвями дерева; [Q_L,e] – блок матрицы [Q_L], соответствующий главным сечениям, образованным источниками ЭДС; [Q_L,C] – блок матрицы [Q_L], соответствующий главным сечениям, образованным ёмкостными ветвями; [Q_L,rд] – блок матрицы [Q_L], соответствующий главным сечениям, образованным резистивными ветвями дерева; [Q_J,e] – блок матрицы [Q_J], соответствующий главным сечениям, образованным источниками ЭДС; [Q_J,C] – блок матрицы [Q_J], соответствующий главным сечениям, образованным ёмкостными ветвями; [Q_J,rд] – блок матрицы [Q_J], соответствующий главным сечениям, образованным резистивными ветвями дерева.

Развернём соотношения (5) и выразим токи и напряжения по категориям ветвей:

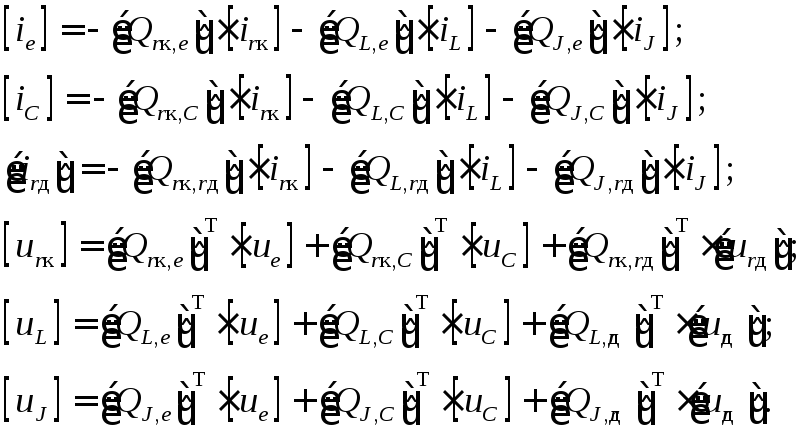
Используя последние соотношения и выражения (6), выразим [i_rк] и [u_rд] через [u_e], [i_J], , [q_C]:

Введём обозначение [g^(к)] – матрица проводимостей главных контуров, образованных резистивными ветвями связи, [r^(c)] – матрица сопротивлений главных сечений, образованных резистивными ветвями дерева:

,

.

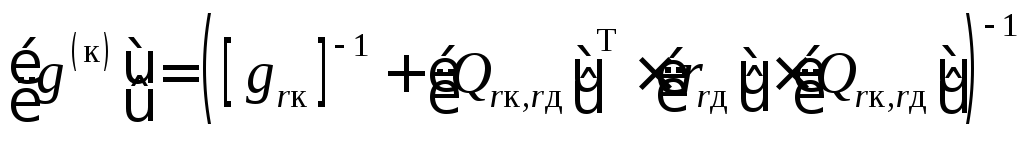Будем предполагать, что положительные направления источников ЭДС и тока совпадают с положительными направлениями ветвей, тогда

[u_e]=-[e^(в)], [i_J]=[J^(в)].

Для линейных электрических цепей дифференциальные уравнения относительно переменных состояния имеют вид

,

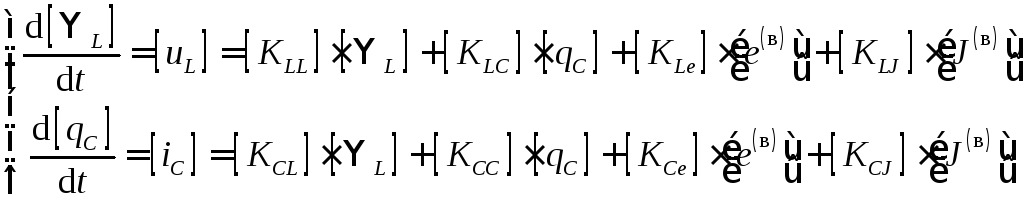где

Для проверки изложенного метода рассмотрим схему электрической цепи, изображённую на рис.1. Жирными линиями выделены ветви дерева. Пусть L=1 Гн, C=0.04 мкФ, R_i=1 кОм, e(t)=1(t) B.

Для формирования и решения уравнений относительно переменных состояния цепи, изображённой на рис.1, использована система MATLAB, решатель дифференциальных уравнений – ode15s. Переходный процесс в цепи рассчитывался при нулевых начальных условиях (в начальный момент времени потокосцепление индуктивного элемента и заряд конденсатора равны нулю). На рис.2 представлены осциллограммы переменных состояния цепи во время переходного процесса. На нис.3 – осциллограммы относительной погрешности численного (методом ode15s) расчёта переменных состояния.

Осциллограммы, изображённые на рис.2,3 подтверждают работоспособность предложенного метода моделирования переходных процессов в линейных электрических цепях.

Рис.1. Схема, содержащая два реактивных элемента

Рис.2. Осциллограммы переменных состояния

Рис.3. Относительная погрешность моделирования

УДК 621.3.01: 518.12

В.Е. Шмелёв