
КСИТ, МЭФП / Dista_MEFP / Lekcii_MEFP
.pdfМоделирование электрофизических процессов в устройствах и системах
электроэнергетики
ЭФП – электрофизический процесс. ЭМП – электромагнитное поле.
ODE – обыкновенное дифференциальное уравнение.
PDE – Partial differential equation – дифференциальное уравнение в частных производных.
Понятие об электрофизических процессах, классификация методов их
математического и компьютерного моделирования
К электрофизическим относят все электромагнитные процессы, а также совокупность электромагнитных процессов и физических процессов другой природы, связанных с явлениями электромагнетизма. Электрофизика изучает все виды электромагнитных полей (ЭМП), режимы работы электрических и магнитных цепей, сетей и устройств. Этот раздел науки изучает все явления, связанные с протеканием электрического тока в проводниках, полупроводниках, диэлектриках, силовые взаимодействия в электрических и магнитных полях, явления поляризации и намагничивания физических тел в электромагнитных полях и под действием неэлектромагнитных факторов: механическое движение, тепловое поле, механические напряжения, химические реакции и превращения, фазовые переходы и структурные изменения в веществе. Электрофизика изучает также движение заряженных частиц и поведение плазмы в электромагнитных полях и др.
Краткая классификация методов математического моделирования элек-
трофизических процессов.
Существуют методы математического моделирования на интегральном уров-
не и на пространственнораспределённом уровне. Первая группа методов математически описывает процессы с помощью интегральных физических величин (токи, напряжения, магнитные потоки, потокосцепления, заряды, мгновенные, полные, активные, неактивные мощности, энергии в конечных объёмах, усреднённые температуры, давления и концентрации, интегральные силы и моменты и др.).
Вторая группа методов математически описывает процессы с помощью пространственнораспределённых физических величин (векторы и потенциалы электромагнитного поля, пространственные распределения скоростей, ускорений, температур, давлений, концентраций, объёмных плотностей мощностей, энергий, зарядов, плотностей потоков мощностей и др.).
Существуют также группы методов моделирования ЭФП во временной и в частотной области. Первая из этих групп методов базируется на уравнениях, в которые время входит в явном виде. Вторая из этих групп методов базируется на уравнениях, в которые время не входит, но входит частота синусоидальных колебаний; все физические величины представляются не мгновенными значениями, а их комплексными амплитудами или комплексными действующими значениями. Если моделируемый процесс не стационарный и не периодический, т.е. обладает непрерывным частотным спектром, то физиче-
ские величины в частотных методах заменяются комплексными спектральными плотностями.
Среди методов математического моделирования на интегральном уровне можно выделить схемотехнические методы и структурные методы.
Методы математического моделирования на пространственнораспределённом уровне базируются на дифференциальных уравнениях в частных производных (PDE).
Схемотехнические методы
Эти методы основаны на построении электрических, магнитных или электромагнитных схем замещения моделируемого объекта и последующем анализе режимов и процессов методами теории цепей. Если схема замещения достаточно сложная, то при анализе применяются топологические соотношения в матричной форме.
Схемотехнические методы моделирования электрофизических процессов достаточно подробно рассмотрены в дисциплине «Теоретические основы электротехники» (теория цепей).
Отметим только, что топологические соотношения могут быть использованы и для анализа режимов нелинейных цепей экономичными методами: узловых потенциалов, контурных токов, напряжений ветвей дерева.
Если это метод узловых потенциалов, то нелинейное матричное уравнение состояния цепи имеет вид
f ( ϕ(y) )= 0, |
(1) |
где нелинейная функция f в левой части уравнения (1) вычисляет алгебраические суммы токов ветвей, присоединённых к не общим узлам по задаваемым значениям узловых потенциалов. В результате выполнения итерационной процедуры определяются узловые потенциалы, удовлетворяющие уравнению
(1) с некоторой заданной точностью сходимости. Если столбец вольтамперных характеристик пассивных участков ветвей обозначить g ( Uп(в) ), то оп-
ределяющее матричное выражение для функции f, входящей в (1), имеет вид
|
(y) |
|
T |
|
(y) |
|
(в) |
|
(в) |
|
f ( j |
)= |
[A]× (g ([A] |
× j |
|
+ E |
|
)- |
J |
), |
|
где [A] – матрица узловых соединений; |
ϕ(y) |
– столбец узловых потенциа- |
||||||||
|
|
|
|
|
|
|
|
|
|
|
лов; |
E |
(в) – |
столбец ЭДС ветвей; |
J (в) |
|
– столбец источников тока ветвей. |
||||
|
|
|
|
|
|
|
|
|
|
|
Нелинейное матричное уравнение состояния цепи в методе напряжений ветвей дерева имеет вид
f ( U (д) )= 0, |
(2) |
где нелинейная функция f в левой части уравнения (2) вычисляет алгебраические суммы токов ветвей, принадлежащих главным сечениям цепи по зада-
ваемым значениям напряжений ветвей дерева. Определяющее матричное выражение для функции f, входящей в (2), имеет вид
f ( U (д) )= [Q]× (g ([Q]T × U (д) + E(в) )- J (в) ),
где [Q] – матрица главных сечений; U (д) – столбец напряжений ветвей де-
рева.
Нелинейное матричное уравнение состояния цепи в методе контурных токов имеет вид
f ( I (к) )= 0, |
(3) |
где нелинейная функция f в левой части уравнения (3) вычисляет алгебраические суммы напряжений ветвей, принадлежащих главным контурам цепи по задаваемым значениям контурных токов (токов ветвей связи). Если столбец вольтамперных характеристик пассивных участков ветвей обозначить
r ( Iп(в) ), то определяющее матричное выражение для функции f, входящей в
(3), имеет вид
f ( I (к) )= [B]×(r ([B]T × I (к) + J (в) )- E(в) ),
где [B] – матрица главных контуров; I (к) – столбец токов ветвей связи.
Уравнения (1), (2), (3) пригодны для моделирования статических режимов работы нелинейных электрических и магнитных цепей, т.е. таких установившихся режимов, когда ЭДС и токи источников либо не изменяются во времени, либо для любого момента времени текущее состояние цепи определяется только мгновенными значениями ЭДС и токов источников и не зависит от временных производных и первообразных этих величин. Статические режимы при переменных ЭДС и токах источников возможны только тогда, когда пассивные элементы цепи обладают чисто резистивными свойствами.
Если электрическая схема замещения содержит индуктивные и ёмкостные элементы, то процессы в таких цепях описываются не алгебраическими, а дифференциальными уравнениями (ДУ). Если моделируемая цепь с сосредоточенными параметрами, то процессы в ней описываются обыкновенными дифференциальными уравнениями (ODE). Для решения ODE существуют стандартные решатели (например, в системе MATLAB), реализующие численные методы. Наиболее корректно эти решатели подключаются, если система ODE цепи сформирована методом переменных состояния. В качестве переменных состояния лучше всего выбирать магнитные потокосцепления идеальных индуктивных элементов и заряды идеальных ёмкостных элементов. Первые производные по времени от этих физических величин представляют собой напряжения на зажимах индуктивностей и токи в ёмкостях. В соответствии со сказанным, система уравнений электрической цепи с сосредоточенными параметрами в пространстве состояний имеет вид
[u |
L |
] |
|
[Ψ |
L |
] |
|
|
(в) |
(в) |
|
|
|
|||||||||
|
|
[i |
] = f1 |
|
[q |
|
, |
|
|
|
||||||||||||
|
|
|
] |
e |
, |
J |
|
|
|
|||||||||||||
|
|
|
|
|
C |
|
|
|
C |
|
|
|
|
|
|
|
|
|
, |
|||
|
|
|
|
|
(в) |
|
|
[ΨL ] |
, e(в) |
, J (в) |
|
|
||||||||||
|
|
u |
|
|
|
= f |
|
|
|
(4) |
||||||||||||
|
|
|
i |
(в) |
|
|
2 |
[q |
] |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где [uL] – |
столбец мгновенных напряжений на зажимах идеальных индук- |
|||||||||||||||||||||
тивных элементов; [iC] – |
столбец мгновенных токов в идеальных ёмкостных |
|||||||||||||||||||||
элементах; |
f1 – |
нелинейная функция передач от переменных состояния и |
||||||||||||||||||||
мгновенных параметров источников к скоростям изменения переменных состояния; [ΨL ] – столбец мгновенных потокосцеплений в идеальных нели-
нейных индуктивностях; |
[qC ] |
– |
столбец мгновенных зарядов в идеальных |
||
нелинейных ёмкостях; |
Ψ |
|
– |
столбец мгновенных значений переменных |
|
[[q L]] |
|
||||
|
|
C |
|
|
|
состояния моделируемой цепи; e(в) – столбец мгновенных значений ЭДС ветвей; J (в) – столбец мгновенных значений токов источников ветвей;
u(в) – столбец мгновенных значений напряжений ветвей; i(в) – столбец
мгновенных значений токов ветвей; f2 – нелинейная функция передач от переменных состояния и мгновенных параметров источников к напряжениям и токам ветвей.
Пусть схема замещения цепи состоит из нелинейных идеализированных двухполюсников: резистивных, индуктивных и ёмкостных, а также идеальных источников ЭДС и тока. Чтобы построить удобный способ матричного представления нелинейных функций f1 и f2, входящих в уравнения (4), нужно при описании топологии цепи каждый двухполюсник считать отдельной ветвью, причём все источники ЭДС и ёмкостные элементы должны являться ветвями дерева, т.к. напряжения на зажимах источников ЭДС всегда известны, а напряжения на зажимах емкостных элементов функционально (кулонвольтными характеристиками) связаны с зарядами, которые являются входными аргументами нелинейных функций f1 и f2. Все источники тока и индуктивные элементы должны являться ветвями связи, т.к. токи источников тока всегда известны, а токи индуктивных элементов функционально (веберам- перными характеристиками) связаны с магнитными потокосцеплениями, которые являются входными аргументами нелинейных функций f1 и f2. Резистивные элементы могут быть как ветвями дерева, так и ветвями связи.
В связи с изложенными соображениями все ветви схемы замещения нужно разделять на 6 групп: 1) ветви дерева с идеальными источниками ЭДС, 2) ветви дерева с идеальными ёмкостями, 3) резистивные ветви дерева, 4) резистивные ветви связи, 5) ветви связи с идеальными индуктивностями, 6) ветви связи с идеальными источниками тока. Наиболее удобным компьютерным
представлением топологии цепи является матрица узловых соединений [A], которую можно представить в виде горизонтальной склейки двух блоков: 1) узловая матрица ветвей дерева [Aд], 2) узловая матрица ветвей связи [Aк]. Для вывода определяющих матричных выражений функций f1 и f2 наиболее удобна матрица главных сечений [Q], которая может быть получена из матрицы [A].
[Q]= Q |
,[Q |
] |
= A −1 × |
A |
,[A |
] |
= 1 |
, A −1 |
×[A |
] |
; |
||
д |
к |
|
|
д |
|
д |
к |
|
д |
д |
к |
|
|
Матрица главных контуров: |
|
|
|
|
|
|
|
|
|||||
[B]= B |
,[B |
] |
= -[Q ]T |
,[1 |
] , |
|
|
|
|
|
|
||
д |
к |
|
|
к |
к |
|
|
|
|
|
|
|
|
где [Qд]=[1д] – блок матрицы [Q], соответствующий только ветвям дерева, [1д] – единичная матрица размера (д,д), где д – число ветвей дерева; [Qк] – блок матрицы [Q], соответствующий только ветвям связи; [Bд] – блок матрицы [B], соответствующий только ветвям дерева, [Bк]=[1к] – блок матрицы [B], соответствующий только ветвям связи, [1к] – единичная матрица размера (к,к), где к – число ветвей связи. Последние соотношения показывают, что для записи обоих законов Кирхгофа достаточна только одна матрица [Qк]. С помощью этой матрицы выразим по первому закону Кирхгофа токи ветвей дерева через токи ветвей связи и по второму закону Кирхгофа выразим напряжения ветвей связи через напряжения ветвей дерева:
[i |
] |
[i |
|
] |
|
[u |
rк |
] |
[u |
e |
] |
|
||||||
|
e |
] |
= -[Q ]× |
rк |
] |
|
|
|
] |
= [Q ]T × |
[u |
|
] , |
|
||||
[i |
[i |
|
, |
|
[u |
|
|
|
(5) |
|||||||||
|
i |
|
|
[i |
L |
] |
|
|
[u |
L |
] |
|
u |
C |
|
|||
|
C |
|
к |
|
|
|
|
|
|
|
к |
|
|
|||||
rд |
|
J |
|
J |
rд |
|
|
где [ie] – |
матрицастолбец токов, протекающих через источники ЭДС; [iC] – |
||||||
матрицастолбец токов, протекающих через идеальные ёмкости; |
[irд] матри- |
||||||
цастолбец токов, протекающих через резистивные ветви дерева; |
[irк] – |
мат- |
|||||
рицастолбец токов, протекающих через резистивные ветви связи; [iL] – |
|
||||||
матрицастолбец токов, протекающих через идеальные индуктивности; |
[iJ] – |
||||||
матрицастолбец токов, протекающих через идеальные источники тока; |
[urк] |
||||||
– матрицастолбец напряжений на резистивных ветвях связи; [uL] – матрицастолбец напряжений на идеальных индуктивностях; [uJ] – матрицастолбец напряжений на идеальных источниках тока; [ue] – матрицастолбец напряжений на идеальных источниках ЭДС; [uC] – матрицастолбец напряжений на идеальных ёмкостях; [urд] – матрицастолбец напряжений на резистивных ветвях дерева. В общем случае взаимосвязи между величинами [iL] и [ΨL ],
[uC] и [qC], [irк] и [urк], [irд] и [urд] являются нелинейными. Именно эти нелинейности обуславливают нелинейный характер функций f1, f2, входящих в уравнения (4). Далее рассмотрим случай, когда эти взаимосвязи линейные:
[irк ] = [ grк ] ×[urк ]
u |
|
= r |
× i |
|
rд |
rд |
rд |
;[iL ] = [ L]−1 ×[YL ] ,
; |
[u |
] = [C]−1 ×[q |
(6) |
], |
|||
|
C |
C |
|
где [grк] – матрица проводимостей резистивных ветвей связи (в простейшем случае диагональная); [L] – матрица индуктивностей ветвей; [rrд] – матрица сопротивлений резистивных ветвей дерева; [C] – матрица ёмкостей ветвей. Чтобы развернуть блочноматричные соотношения (5), матрицу [Qк] представим склейкой блоков:
[Qк ] = [Qrк
|
|
|
Q |
|
],[Q |
],[Q ] |
= |
|
rк,e |
Q |
||||
L |
J |
|
|
rк,C |
|
|
|
|
Q |
|
|
|
|
rк,rд |
|
Q |
|
L,e |
|
Q |
|
L,C |
|
Q |
|
L,rд |
|
Q |
|
J ,e |
|
Q |
|
J ,C |
|
Q |
|
J ,rд |
,
где [Qrк] – блок матрицы [Qк], соответствующий только резистивным ветвям связи; [QL] – блок матрицы [Qк], соответствующий только индуктивным ветвям; [QJ] – блок матрицы [Qк], соответствующий только ветвям с идеальными источниками тока; [Qrк,e] – блок матрицы [Qrк], соответствующий главным сечениям, образованным источниками ЭДС; [Qrк,C] – блок матрицы [Qrк], соответствующий главным сечениям, образованным ёмкостными ветвями; [Qrк,rд] – блок матрицы [Qrк], соответствующий главным сечениям, образованным резистивными ветвями дерева; [QL,e] – блок матрицы [QL], соответствующий главным сечениям, образованным источниками ЭДС; [QL,C] – блок матрицы [QL], соответствующий главным сечениям, образованным ёмкостными ветвями; [QL,rд] – блок матрицы [QL], соответствующий главным сечениям, образованным резистивными ветвями дерева; [QJ,e] – блок матрицы [QJ], соответствующий главным сечениям, образованным источниками ЭДС; [QJ,C] – блок матрицы [QJ], соответствующий главным сечениям, образованным ёмкостными ветвями; [QJ,rд] – блок матрицы [QJ], соответствующий главным сечениям, образованным резистивными ветвями дерева. Развернём соотношения (5) и выразим токи и напряжения по категориям ветвей:
[i |
|
] |
= - Q |
|
×[i |
] - Q |
× |
[i |
L |
] - Q |
|
×[i |
J |
]; |
|
|
|
|
|||||||||||||||
e |
|
|
|
|
|
rк,e |
|
rк |
|
|
|
L,e |
|
|
|
|
|
|
|
J ,e |
|
|
|
|
|
|
|
|
|||||
[i |
|
] = - Q |
|
×[i |
|
] |
- Q |
|
×[i ] |
- Q |
× |
[i |
J |
]; |
|
|
|
||||||||||||||||
C |
|
|
|
|
rк,C |
rк |
|
|
L,C |
|
|
|
L |
|
|
|
|
|
J ,C |
|
|
|
|
|
|
|
|||||||
i |
|
|
|
= - |
Q |
|
|
×[i |
|
] - |
Q |
|
|
|
×[i |
L |
] - Q |
|
×[i |
J |
]; |
|
|||||||||||
rд |
|
|
rк,rд |
|
rк |
|
L,rд |
|
|
|
|
|
J ,rд |
|
|
|
|
|
|
||||||||||||||
[u |
rк |
] = Q |
T |
×[u |
] |
+ Q |
T |
×[u |
|
] + |
Q |
|
T × |
u |
; |
||||||||||||||||||
|
|
|
rк,e |
|
|
e |
|
|
rк |
,C |
|
|
|
|
C |
|
|
|
rк,rд |
|
|
|
|
rд |
|||||||||
[u |
L |
] |
= Q |
T |
×[u |
] + Q |
T |
× |
[u |
|
] |
+ |
Q |
T × u |
rд |
; |
|||||||||||||||||
|
|
|
|
L,e |
|
|
e |
|
|
|
L,C |
|
|
|
C |
|
|
|
|
L,rд |
|
|
|
|
|
||||||||
[u |
J |
] |
= Q |
T |
×[u |
] + Q |
T |
× |
[u |
|
|
] |
+ |
Q |
T × u |
rд |
. |
||||||||||||||||
|
|
|
|
J ,e |
|
|
e |
|
|
|
J ,C |
|
|
|
C |
|
|
|
|
J ,rд |
|
|
|
|
|
||||||||
Используя последние соотношения и выражения (6), выразим [irк] и [urд] че-
рез [ue], [iJ], [ΨL ], [qC]:
[i |
|
|
]= |
( |
[g |
rк |
]−1 |
+ |
Q |
|
|
|
T |
× r |
|
× |
Q |
|
|
|
|
|
−1 × |
|
|
|
|
|||||||||||||
|
rк |
|
|
|
|
|
|
|
|
|
|
rк |
,rд |
rд |
|
|
|
rк |
,rд ) |
|
|
|
|
|
|
|||||||||||||||
× |
( |
Q |
|
T × |
[u |
] |
+ Q |
|
|
T ×[C ]−1 ×[q |
|
]+ |
Q |
T × r × |
|
|||||||||||||||||||||||||
|
|
|
rк,e |
|
|
|
|
e |
|
|
|
|
rк,C |
|
|
|
|
|
|
|
C |
|
)) |
|
|
rк,rд |
rд |
|
|
|||||||||||
× |
( |
- Q |
|
×[L]−1 ×[Y |
L |
]- Q |
|
|
|
×[i |
J |
] |
; |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
L,rд |
|
|
|
|
|
|
|
|
|
|
|
J ,rд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
u |
|
= |
( |
r |
|
−1 |
+ |
Q |
|
|
|
×[g |
rк |
] |
× |
Q |
|
|
T |
) |
−1 |
× |
|
|
|
|||||||||||||||
|
|
rд |
|
rд |
|
|
|
|
|
rк,rд |
|
|
|
|
|
rк,rд |
|
|
|
|
|
|
||||||||||||||||||
× |
( |
- Q |
|
|
|
|
×[g |
rк |
] |
× |
( |
Q |
|
T ×[u |
]+ |
Q |
|
|
T ×[C ]−1 |
×[q ] |
) |
- |
||||||||||||||||||
|
|
|
|
|
rк,rд |
|
|
|
|
|
|
|
rк,e |
|
|
e |
|
|
|
|
|
|
rк,C |
|
|
|
C |
|
||||||||||||
- |
Q |
|
|
×[L]−1 |
×[Y |
L |
]- Q |
×[i |
J |
] |
|
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
L,rд |
|
|
|
|
|
|
|
|
|
|
|
|
|
J ,rд |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
||||||||
Введём обозначение [g(к)] – матрица проводимостей главных контуров, образованных резистивными ветвями связи, [r(c)] – матрица сопротивлений главных сечений, образованных резистивными ветвями дерева:
g |
(к) |
= |
( |
[g |
|
]−1 |
+ Q |
T × r |
|
× Q |
|
|
−1 |
|||
rк |
|
, |
||||||||||||||
|
|
|
|
|
|
rк,rд |
rд |
rк,rд ) |
|
|||||||
r |
(c) |
= |
r |
−1 |
+ Q |
|
×[g |
rк |
]× |
Q |
T |
) |
−1 . |
|||
|
|
|
|
( rд |
rк,rд |
|
|
rк,rд |
|
|||||||
Будем предполагать, что положительные направления источников ЭДС и тока совпадают с положительными направлениями ветвей, тогда
[ue]=-[e(в)], [iJ]=[J(в)].
Для линейных электрических цепей дифференциальные уравнения относительно переменных состояния имеют вид
|
d[YL ] |
= [u ]= [K |
|
|
]×[Y |
|
|
]+ [K |
|
|
]×[q ]+ [K |
|
|
]× |
e(в) + [K |
|
]× |
J (в) |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
dt |
|
|
L |
|
|
|
|
LL |
|
|
|
L |
|
|
|
LC |
|
C |
|
|
Le |
|
|
|
|
|
LJ |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
d[qC ] |
= |
[i |
]= [K |
|
|
]×[Y |
|
|
]+ [K |
|
|
]×[q ]+ |
[K |
|
|
]× e(в) |
+ [K |
|
|
]× |
J |
(в) , |
||||||||||||||||||||||
|
CL |
L |
CC |
Ce |
CJ |
||||||||||||||||||||||||||||||||||||||||
|
dt |
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
[K |
LL |
]= - Q |
|
T |
× |
r |
(c) |
|
× Q |
|
|
|
×[L]−1 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
L,rд |
|
|
|
|
|
|
L,rд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
[K |
LC |
]= |
( |
Q |
|
|
T |
- |
Q |
|
|
T × |
r |
(c) × Q |
|
× |
[g |
rк |
]× Q |
|
T |
) |
×[C ]−1 ; |
||||||||||||||||||||||
|
|
|
|
|
|
|
L,C |
|
|
|
L,rд |
|
|
|
|
|
rк,rд |
|
|
|
|
rк,C |
|
|
|
|
|
||||||||||||||||||
[K |
Le |
]= - |
Q |
T |
- Q |
|
|
|
T × r(c) |
× Q |
|
|
×[g |
rк |
]× |
Q |
|
T |
) |
; |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
( |
|
|
L,e |
|
|
|
|
L,rд |
|
|
|
|
rк,rд |
|
|
|
|
rк,e |
|
|
|
|
||||||||||||||||
[K |
LJ |
] = - |
Q |
|
T × r(c) |
× Q |
|
; |
|
||||
|
|
|
L,rд |
|
|
|
J ,rд |
|
|
||||
[K |
CL |
] = - |
( |
Q |
|
|
- Q |
|
× g |
(к) |
× Q |
||
|
|
L,C |
|
rк,C |
|
|
|
rк,rд |
|||||
[K |
CC |
] = - Q |
|
|
× g (к) |
× Q |
T |
×[C ]−1 ; |
|||||
|
|
rк,C |
|
|
|
rк,C |
|
|
|||||
[K |
Ce |
] = Q |
|
× g (к) |
× Q |
T ; |
|
|
|||||
|
|
|
rк,C |
|
|
|
|
rк,e |
|
|
|
||
[K |
CJ |
] = - |
( |
Q |
|
|
- Q |
|
× g |
(к) |
× Q |
||
|
|
|
J ,C |
|
rк,C |
|
|
|
rк,rд |
||||
T × r |
|
× Q |
|
×[L]−1 ; |
||
|
rд |
|
L,rд ) |
|
||
T × r |
|
× Q |
|
; |
|
|
rд |
|
J ,rд ) |
|
|
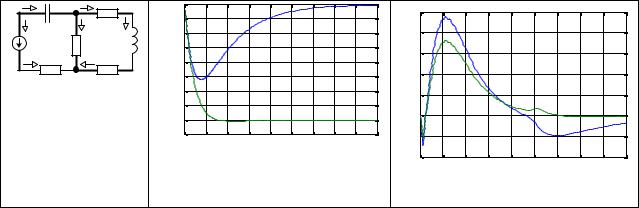
Для проверки изложенного метода рассмотрим схему электрической цепи, изображённую на рис.1. Жирными линиями выделены ветви дерева.
Пусть L=1 Гн, C=0.04 мкФ, Ri=1 кОм, e(t)=1(t) B.
Для формирования и решения уравнений относительно переменных состояния цепи, изображённой на рис.1, использована система MATLAB, решатель дифференциальных уравнений – ode15s. Переходный процесс в цепи рассчитывался при нулевых начальных условиях (в начальный момент времени потокосцепление индуктивного элемента и заряд конденсатора равны нулю). На рис.2 представлены осциллограммы переменных состояния цепи во время переходного процесса. На нис.3 – осциллограммы относительной погрешности численного (методом ode15s) расчёта переменных состояния.
Осциллограммы, изображённые на рис.2,3 подтверждают работоспособность предложенного метода моделирования переходных процессов в линейных электрических цепях.
|
|
0 |
|
|
|
|
|
|
|
|
|
|
-8 |
|
|
|
|
|
|
|
|
|
|
Потокосцепление, мВб; Заряд, мкКл |
|
|
|
|
|
|
|
|
|
|
x 10 |
|
|
|
|
|
|
|
|
|
|
|
-0.005 |
|
|
|
|
|
|
|
|
|
Относительная погрешность моделирования |
2.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Относительная погрешность потокосцепления |
|
|
||||||||
|
-0.01 |
|
|
|
|
|
|
|
|
|
2 |
|
индуктивного элемента |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
-0.015 |
|
|
|
|
|
|
|
|
|
1.5 |
|
|
|
|
|
|
|
|
|
||
|
|
|
потокосцепление индуктивного элемента, мВб |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
-0.02 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
-0.025 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
Рис.1. Схема, содер- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
-0.03 |
|
|
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
Относительная погрешность |
||||||
жащая два реактивных |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
-0.035 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
заряд конденсатора, мкКл |
|
|
|
|
|
|
|
заряда конденсатора |
|
|||||||||
элемента |
-0.04 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
-0.045 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
1.2 |
1.4 |
1.6 |
1.8 |
-0.5 |
|
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
Время, мс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Рис.2. Осциллограммы переменных со- |
|
-1 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
1.2 |
1.4 |
1.6 |
1.8 |
||||||||||
|
|
0 |
||||||||||||||||||||
|
|
|
|
|
стояния |
|
|
|
|
|
|
|
|
|
Время, мс |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Рис.3. Относительная погрешность мо- |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
делирования |
|
|
|
|
|
|
|
|||
УДК 621.3.01: 518.12
В.Е. Шмелёв
Моделирование переходных процессов в нелинейных электрических цепях методом
переменных состояния на базе матричных топологических соотношений
Аннотация Предложен метод и вычислительный алгоритм автоматизации построения системы
уравнений относительно переменных состояния нелинейной электрической цепи произвольной сложности, если цепь представлена схемой замещения, содержащей идеализированные источники ЭДС и тока, индуктивные, ёмкостные и резистивные элементы. Предложенный метод базируется на топологических соотношениях теории цепей в матричной форме. Принята стандартная система переменных состояния: потокосцепления индуктивных элементов и заряды ёмкостных элементов. Входы модели (динамической системы) – ЭДС и токи источников. Выходы модели – напряжения и токи всех ветвей (элементов схемы замещения). Входные данные разработанного алгоритма – матрица узловых соединений, кодирующая схему замещения; шесть списков номеров: ветвей дерева с идеальными источниками ЭДС, ёмкостных ветвей дерева, резистивных ветвей дерева, резистивных ветвей связи, индуктивных ветвей связи, ветвей с идеальными источниками тока; дескрипторы функций времени, представляющих ЭДС и токи источников; дескрипторы нелинейных функций, представляющих характеристики свойств всех остальных элементов. Выходные данные разработанного алгоритма – дескрипторы нелинейных функций передач от входов динамической системы и переменных состояния к скоростям изменения переменных состояния, а также к выходам моделируемой системы (цепи). В статье предложено также два новых метода статического анализа нелинейных электрических цепей: метод напряжений резистивных ветвей связи и метод токов резистивных ветвей дерева. Эти методы применены для автоматизации построения дескрипторов нелинейных функций, входящих в типовую матричную форму модели цепи в пространстве состояний. Вычислительные эксперименты подтверждают работоспособность предложенных методов и алгоритмов.
Ключевые слова: нелинейная электрическая цепь, переходные процессы, метод переменных состояния, топология, методы нелинейного статического анализа.
Abstract
The method and computing algorithm of automation of build of simultaneous equations concerning state variables of the nonlinear electric circuit of any complexity if the circuit is presented by an equivalent circuit containing idealized sources of the EMF and a current, inductive,
capacitor and resistive elements is offered. The offered method is based on topological parities of circuit theory in the matrix form. The standard system of state variables is accepted: magnetic flux linkage inductive elements and charges of capacitor elements. Model inputs (dynamic system) – the EMF and currents of sources. Model outpu ts – voltages and currents of all branches (equivalent circuit elements). The input data of the developed algorithm - the matrix of node connections coding an equivalent circuit; six lists of numbers: branches of a tree with ideal sources of the EMF, capacitor branches of a tree, resistive branches of a tree, resistive branches of chord, inductor branches of chord, branches with ideal current sources; descriptors of time functions representing the EMF and currents of sources; descriptors of the nonlinear functions representing the characteristics of properties of all other elements. Output data of the developed algorithm – descriptors of nonlinear functions of t ransfers from inputs of dynamic system and state variables to speeds of change of state variables, and also to exits of modeled system (circuit). In article it is offered also two new methods of the static analysis of nonlinear electric circuits: a method of chord resistive branches voltages and a method of tree resistive branches currents. These methods are applied to automation of build of descriptors of the nonlinear functions entering into the typical matrix form of circuit model in a state space. Computing experiments confirm working capacity of the offered methods and algorithms.
Key words: nonlinear electric circuit, transients, the method the state variables, topology, methods of nonlinear static analysis.
Важным этапом автоматизированного проектирования электронных средств является проведение поверочных расчётов, которые часто сводятся к моделированию переходных и установившихся режимов [1, 2]. Электронные средства содержат электрические и магнитные цепи, которые при моделировании представляются схемами замещения [3 – 13 и др.].
Если схема замещения электрической цепи содержит индуктивные и ёмкостные элементы, то процессы в таких цепях описываются дифференциальными уравнениями (ДУ) [3,4,6–13 и др.]. Если моделируемая цепь с сосредоточенными параметрами, то процессы в ней описываются обыкновенными дифференциальными уравнениями (ODE). Для решения ODE существуют стандартные решатели (например, в системе MATLAB) [14], реализующие численные методы, которые в настоящее время продолжают совершенствоваться [15,16 и др.]. Наиболее корректно эти решатели подключаются, если система ODE цепи сформирована методом переменных состояния [17]. В качестве переменных состояния лучше всего выбирать магнитные потокосцепления идеальных индуктивных элементов и заряды идеальных ёмкостных элементов [7 – 13, 18 – 20]. Первые производные по време-
