Lekcii_MEFP

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Владимирский государственный университет им. Столетовых

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

,[e],[iJ ] , (4)

.pdf

Скачиваний:

Добавлен:

22.03.2015

Размер:

477.63 Кб

Скачать

☆

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

ни от этих физических величин представляют собой напряжения на зажимах индуктивностей и токи в ёмкостях. В соответствии со сказанным, система уравнений электрической цепи с сосредоточенными параметрами в пространстве состояний имеет вид

]

= f

[Ψ

]

) , J

)

]

(

]

(1)

u(в)

[Ψ

]

)

= f

(

(в)

]

, e

, J

где

[uL] –

столбец мгновенных напряжений на зажимах идеальных индуктивных элемен-

тов;

[iC] –

столбец мгновенных токов в идеальных ёмкостных элементах;

f1 – нелинейная

функция передач от переменных состояния и мгновенных параметров источников к ско-

ростям изменения переменных состояния;				[ΨL ]	–	столбец мгновенных потокосцеплений в
идеальных нелинейных индуктивностях;				[qC ] –	столбец мгновенных зарядов в идеальных
		Ψ
нелинейных ёмкостях;		[[qCL]] – столбец мгновенных значений переменных состояния мо-
делируемой цепи;	e(в) –		столбец мгновенных значений ЭДС ветвей;					J (в) – столбец

мгновенных значений токов источников ветвей;						u	(в) – столбец мгновенных значений

напряжений ветвей;	i	(в) –	столбец мгновенных значений токов ветвей;					f2 –	нелинейная

функция передач от переменных состояния и мгновенных параметров источников к напряжениям и токам ветвей.

Пусть схема замещения цепи состоит из нелинейных идеализированных двухполюсников: резистивных, индуктивных и ёмкостных, а также идеальных источников ЭДС и тока. Чтобы построить удобный способ матричного представления нелинейных функций f1 и f2, входящих в уравнения (1), нужно при описании топологии цепи каждый двухполюсник считать отдельной ветвью [7, 13], причём все источники ЭДС и ёмкостные элементы должны являться ветвями дерева, т.к. напряжения на зажимах источников ЭДС всегда известны, а напряжения на зажимах ёмкостных элементов функционально (кулонвольтными характеристиками) связаны с зарядами, которые являются входными аргументами нелинейных функций f1 и f2. Все источники тока и индуктивные элементы должны являться ветвями связи, т.к. токи источников тока всегда известны, а токи индуктивных элементов функционально (веберамперными характеристиками) связаны с магнитными потокосцеплениями, которые являются входными аргументами нелинейных функций f1 и f2. Резистивные элементы могут быть как ветвями дерева, так и ветвями связи.

В связи с изложенными соображениями все ветви схемы замещения нужно разделять на 6 групп: 1) ветви дерева с идеальными источниками ЭДС, 2) ветви дерева с идеальными ёмкостями, 3) резистивные ветви дерева, 4) резистивные ветви связи, 5) ветви связи с идеальными индуктивностями, 6) ветви связи с идеальными источниками тока. Наиболее удобным компьютерным представлением топологии цепи является матрица узловых соединений [A], которую можно представить в виде горизонтальной склейки двух блоков [1]: 1) узловая матрица ветвей дерева [Aд], 2) узловая матрица ветвей связи [Aк]. Для вывода определяющих матричных выражений функций f1 и f2 наиболее удобна матрица главных сечений [Q], которая может быть получена из матрицы [A] [7, 8, 9, 13]:

[	Q	]	= Q , Q	= A
[		]	д [ к ]	д

Матрица главных контуров:

[B]= Bд

−1 × Aд		,[Aк ]	= 1д		, Aд −1		×[Aк ]	;

,[Bк ] = -[Qк ]T ,[1к ] ,

где [Qд]=[1д] – блок матрицы [Q], соответствующий только ветвям дерева, [1д] – единичная матрица размера (д,д), где д – число ветвей дерева; [Qк] – блок матрицы [Q], соответствующий только ветвям связи; [Bд] – блок матрицы [B], соответствующий только ветвям дерева, [Bк]=[1к] – блок матрицы [B], соответствующий только ветвям связи, [1к] – единичная матрица размера (к,к), где к – число ветвей связи. Последние соотношения показывают, что для записи обоих законов Кирхгофа достаточна только одна матрица [Qк]. С помощью этой матрицы выразим по первому закону Кирхгофа токи ветвей дерева через токи ветвей связи и по второму закону Кирхгофа выразим напряжения ветвей связи через напряжения ветвей дерева:

]

rк

]

= -[Q

]×

rк

] ,

] = [Q ]T ×

]

(2)

]

rд

где [ie] – матрицастолбец токов,

протекающих через источники ЭДС; [iC] –

матрица-

столбец токов, протекающих через идеальные ёмкости;

[irд] матрицастолбец токов, про-

текающих через резистивные ветви дерева;

[irк] – матрицастолбец токов, протекающих

через резистивные ветви связи;

[iL] –

матрицастолбец токов, протекающих через идеаль-

ные индуктивности;

[iJ] – матрицастолбец токов, протекающих через идеальные источ-

ники тока (в уравнениях (1) обозначено как

J (в) ); [urк] –

матрицастолбец напряжений

на резистивных ветвях связи;

[uL] –

матрица-

столбец напряжений на идеальных индук-

тивностях; [uJ] – матрицастолбец напряжений на идеальных источниках тока;

[ue]=-[e] –

матрицастолбец напряжений на идеальных источниках ЭДС;

[e] – матрицастолбец

ЭДС идеальных источников (в уравнениях (1) обозначено как e(в) ); [uC] – матрица-

столбец напряжений на идеальных ёмкостях; [urд] – матрицастолбец напряжений на резистивных ветвях дерева.

Чтобы развернуть блочноматричные соотношения (2), матрицу [Qк] представим склейкой блоков:

				Q		Q	Q
[Q	]= [Q	],[Q	],[Q ] =		rк,e	L,e	J ,e
[Q	]= [Q	],[Q	],[Q ] =		Q	Q	Q	,
к	rк	L	J	rк,C		L,C	J ,C
					Q	Q	Q
					rк,rд	L,rд	J ,rд

где [Qrк] – блок матрицы [Qк], соответствующий только резистивным ветвям связи; [QL] – блок матрицы [Qк], соответствующий только индуктивным ветвям; [QJ] – блок матрицы [Qк], соответствующий только ветвям с идеальными источниками тока; [Qrк,e] – блок матрицы [Qrк], соответствующий главным сечениям, образованным источниками ЭДС; [Qrк,C]

– блок матрицы [Qrк], соответствующий главным сечениям, образованным ёмкостными ветвями; [Qrк,rд] – блок матрицы [Qrк], соответствующий главным сечениям, образованным резистивными ветвями дерева; [QL,e] – блок матрицы [QL], соответствующий главным сечениям, образованным источниками ЭДС; [QL,C] – блок матрицы [QL], соответствующий главным сечениям, образованным ёмкостными ветвями; [QL,rд] – блок матрицы [QL], соответствующий главным сечениям, образованным резистивными ветвями дерева; [QJ,e] – блок матрицы [QJ], соответствующий главным сечениям, образованным источниками ЭДС; [QJ,C] – блок матрицы [QJ], соответствующий главным сечениям, образованным ёмкостными ветвями; [QJ,rд] – блок матрицы [QJ], соответствующий главным сечениям, образованным резистивными ветвями дерева.

Развернём соотношения (2) и выразим токи и напряжения по категориям ветвей:

] = - Q

×[i

]- Q

×[i

];

rк,e

rк

L,e

J ,e

]= -

×[i

]

- Q

×[i

];

rк,C

rк

L,C

J ,C

= -

×[i

];

rд

rк,rд

rк

L,rд

J ,rд

rк

]= Q

T ×[u

×[u

T × u

;

rк,e

rк,C

rк,rд

rд

]

= Q

×[u

T × u

rд

;

L,e

L,C

L,rд

]

= Q

×[u

T × u

rд

J ,e

J ,C

J ,rд

Используя характеристики свойств нелинейных элементов, запишем уравнения от-

носительно [irд], [urк] при известных [YL], [qC], [ue], [iJ]:

= - Q

×[i

]

(

rк

]

)

- Q

×[i

]

(

]

)

- Q

×[i

rд

rк,rд

rк

L,rд

J ,rд

(3)

T ×[u

]

(

]

)

+ Q

T × u

rк

rк,e

rк,C

rк

,rд

rд (

rд )

где [irк]([urк]) – функциональная зависимость токов резистивных ветвей связи от напряжений этих же ветвей, [urд]([irд]) – функциональная зависимость напряжений резистивных ветвей дерева от токов этих же ветвей, [iL]([YL]) – функциональная зависимость токов индуктивных ветвей от потокосцеплений этих же ветвей, [uC]([qC]) – функциональная зависимость напряжений ёмкостных ветвей от зарядов этих же ветвей. Если первое уравнение (3) подставить во второе, то из системы нелинейных уравнений (3) будет исключено [irд], а если второе уравнение (3) подставить в первое, то из системы нелинейных уравнений (3) будет исключено [urк]. Для экономии вычислительных ресурсов целесообразно исключать более длинный из массивов [irд] или [urк]. С учётом сказанного из уравнений (3) следует два метода статического анализа состояния нелинейной электрической цепи: метод напряжений резистивных ветвей связи и метод токов резистивных ветвей дерева.

Первый из этих методов сводится к формированию и решению матричного уравнения относительно [urк]:

-[u

rк

]- Q

T ×[e]+ Q

×[u

]

(

]

)

rк,e

rк,C

+ Q

T × u

- Q

×[i

]

(

rк

]

)

×[i

]

(

]

)

- Q

×[i

]

= 0.

rк,rд

rд

(

rк,rд

rк

L,rд

J ,rд

)

Далее первое соотношение (3) используется в качестве прямой формулы вычисления [irд]. Второй из этих методов сводится к формированию и решению матричного уравне-

ния относительно [irд]:

- Q		×[i			]	(	- Q
rк,rд			rк							rк,e
- Q	×[i		L	]	(	[Y		L	]	)	-
L,rд

T ×[e]+ Q

T ×[u

]

(

]

)

rк,C

×[i

]- i = 0.

J ,rд

rд


Q	T × u		( i )	)	-
rк,rд		rд	rд	)

Далее второе соотношение (3) используется в качестве прямой формулы вычисления [urк]. Совместное решение уравнений (3) методом напряжений резистивных ветвей связи или методом токов резистивных ветвей дерева обозначим как вспомогательные нелиней-

ные функции:

= f

[Ψ

]

,[e],[i

]

]= f

[Ψ

]

,[e],[i

]

rд

]

rк

]

С учётом введённых обозначений формулы, определяющие нелинейную матричную функцию f1 в системе уравнений (1), имеют вид

d [YL ]

= [u

]= - Q

T ×[e]+ Q

T ×[u

]

(

]

)

+ Q

d t

L,e

L,C

L,rд

×urд

d [qC ]
d [qC ]	= [iC ]= - Qrк,C	×[irк ] f
d t	= [iC ]= - Qrк,C	×[irк ] f	4
d t

×[i

]

(

]

)

- Q

×[i

(5)

J ,C

Формулы, определяющие нелинейную матричную функцию f2 в системе уравнений (1), имеют вид

[ue ]= -[e], [uC ]= [uC ]([qC ]), urд			[Y			]
[ue ]= -[e], [uC ]= [uC ]([qC ]), urд	= urд f	3			L		,[e],[iJ ] ,
				[qC ]

[u	J	]= - Q
	J	J ,e

[ie ]= - Qrк

[urк ]= f4

]

,[e],[iJ

[uL ]= выражение (4),

[q L]

] ,

×[e]+

QJ ,C

[uC ]([qC ])+

QJ ,rд

]

,[e],[iJ

× urд f

] ,

[qC ]

]

,[e],[iJ ]

- QL,e

×[iL ]([YL ])

- QJ ,e

×[iJ ],

×[irк ] f4

[qC ]

]= выражение (5),

= f

]

,[e],[i

]

rд

]

,[e],[iJ

[iL ]= [iL ]([YL ]),

[iJ

]

= J

) .

[irк ]= [irк ] f

] ,

(

[qC ]

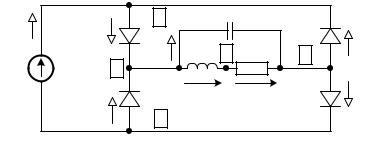
Для проверки работоспособности предложенного метода смоделирован переходный процесс пуска двухполупериодного мостового диодного выпрямителя с ёмкостным и индуктивным фильтром, работающего на резистивную нагрузку (рис.1). Выпрямитель питается от идеального синусоидального источника ЭДС (ветвь №1), амплитуда ЭДС Em=1B,

частота w = 1 рад/мс. Для простоты предположим, что диоды (ветви 2,3,4,5) имеют кусочно- линейную вольтамперную характеристику: проводимость в закрытом состоянии 1 мкСм, проводимость в открытом состоянии 1 См. Сопротивление нагрузки (ветвь 6) Rн=1кОм. Ёмкость фильтра (ветвь 7) C=10мкФ, индуктивный элемент фильтра (ветвь 8) без паразитных параметров с нелинейной безгистерезисной веберамперной характери-

стикой i=2мА×atanh(Y/2мВб), где i – ток, Y – магнитное потокосцепление.

Рис.1. Расчётная схема моделируемого выпрямителя Цифры в прямоугольниках на рис.1 – номера узлов. Ветви 1,2,6,7 – ветви дерева;

3,4,5,8 – ветви связи. Модель переходного процесса реализована в системе MATLAB в виде вычислительного сценария и m-функций. Алгоритм расчёта представляет собой следующую последовательность действий: 1) объявление глобальной переменной для управ-

ления начальным приближением статического нелинейного решателя, 2) задание матрицы узловых соединений моделируемой цепи, 3) задание списков номеров ветвей по категориям (ветви дерева с идеальными источниками ЭДС (в данном случае ветвь 1), ветви дерева с ёмкостными элементами (в данном случае ветвь 7), резистивные ветви дерева (в данном случае ветви 2,6), резистивные ветви связи (в данном случае ветви 3,4,5), ветви связи с индуктивными элементами (в данном случае ветвь 8), ветви связи с идеальными источниками тока (в данном случае пустой список)); 4) инициализация топологической информации (построение списка главных сечений по категориям, построение списка главных контуров по категориям, контроль согласованности топологических параметров, вычисление матрицы [Qк]), 5) настройка параметров нелинейного статического решателя и решателя дифференциальных уравнений, 6) инициализация глобальной переменной, 7) формирование дескрипторов функций времени, описывающих источники ЭДС и тока, дескрипторов функций, описывающих вольтамперные, вебер-амперные и кулонвольтные характеристики пассивных ветвей; 8) формирование дескриптора функции f1 в системе ODE (1) на основе вызова функции статического анализа, вычисляющей параметры состояния ветвей цепи по известным переменным состояния, ЭДС и токов источников; 9) вызов решателя ODE (задачи Коши), 10) повторная инициализация глобальной переменной, 11) завершающий вызов m-функции статического анализа, вычисляющей функцию f2 в системе ODE (1). В системе MATLAB применён решатель дифференциальных уравнений ode15s и статический нелинейный решатель fsolve. Последний вызывается из m-функции нелинейного статического анализа, алгоритм которой основан на применении соотношений (3) и далее. Перед вызовом решателя fsolve строится дескриптор функции, вычисляющей невязку системы нелинейных уравнений относительно токов резистивных ветвей дерева или напряжений резистивных ветвей связи. Сразу после возврата из решателя глобальной переменной присваивается выход решателя fsolve. Это значение будет использоваться при следующем вызове решателя fsolve в качестве начального приближения. Данный вычислительный приём применён для существенного сокращения числа нелинейных статических итераций, которые совершаются на каждом временном шаге в ходе работы решателя ode15s. Такой вычислительный приём может быть осуществлён только путём применения глобальной переменной.

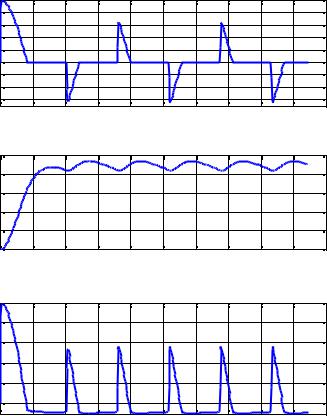
Рассчитанные графики тока в выпрямителе представлены на рис.2.

	10			Входной ток выпрямителя
	10
	8
мА	6
	4
	2
Ток,	2
	0
	-2
	-2
	-4
	-6
	0	2	4	6	8	10	12	14	16	18	20
						Время, мс
	1				Ток нагрузки
	1
мА	0.8
мА	0.6
Ток,	0.4
Ток,	0.2
	0.2
	0	2	4	6	8	10	12	14	16	18	20
	0	2	4	6	8	10	12	14	16	18	20
						Время, мс
	10				Ток конденсатора
	10
	8
мА	6
мА
Ток,	4
Ток,	2
	2
	0
	0	2	4	6	8	10	12	14	16	18	20
						Время, мс

Рис.2. Рассчитанные графики токов Графики, представленные на рис.2, подтверждают работоспособность предложенно-

го метода моделирования переходных процессов в нелинейных электрических цепях, входящих в состав электронных средств. Предложенный метод моделирования отличается от традиционных, основанных на методе переменных состояния, автоматизированным алгоритмом построения нелинейных функций передач от источников ЭДС и токов (входов динамической системы), а также магнитных потокосцеплений и зарядов реактивных элементов (переменных состояния динамической системы) к скоростям изменения переменных состояния, а также к токам и напряжениям всех ветвей. Этот алгоритм основан на матричных топологических соотношениях теории цепей. Предложенный алгоритм позволяет при построении моделей применять стандартные (типовые) решатели ODE и нелинейного статического анализа, содержащиеся в математическом ПО. Кроме того, в данной статье предложены два оригинальных метода статического анализа нелинейных электрических цепей: метод напряжений резистивных ветвей связи и метод токов резистивных ветвей дерева.

Литература 1. Ланцов В.Н. Состояние в области методов моделирования нелинейных ВЧ электронных

устройств связи (Обзор). Часть 1. – Проектирование и технология электронных средств,

2012, № 4. – с. 2 – 11.

2.Павлов Е.П., Санникова И.Т. Основы проектирования электронных средств: Конспект лекций. – Йошкар-Ола: МарГТУ, 2004 – 342 с.

3.Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. – М.: Выс-

шая школа, 1996. – 638 с. ISBN 5-8297-0026-3.

4.Теоретические основы электротехники. Справочник по теории электрических цепей/ Под ред. Ю.А.Бычкова, В.М.Золотницкого, Э.П. Чернышёва. – СПб.: Питер, 2008. – 349 с.

ISBN 978-5-469-00971-9.

5.Жигалов И.Е. Схемотехнический подход к моделированию электромеханических систем. – Проектирование и технология электронных средств, 2013, № 1. – с. 24 – 28.

6.Демирчян К.С., Нейман Л.Р., Коровкин Н.В. Теоретические основы электротехники. –

СПб.: Питер, 2009. – Том 1. – 512 с. ISBN 9785388004109.

7.Демирчян К.С., Коровкин Н.В., Нейман Л.Р. Теоретические основы электротехники. –

СПб.: Питер, 2009. – Том 2. – 431 с. ISBN 9785388004116.

8.Теоретические основы электротехники. Т.1. Основы теории линейных цепей. Под ред. П.А. Ионкина. – М.: Высшая школа, 1976. – 544 с.

9.Зевеке Г.В., Ионкин П.А., Нетушил А.Д., Страхов С.В. Основы теории цепей. – М.:

Энергоатомиздат, 1989. – 528 с. ISBN 5-283-00523-2.

10.Башарин С.А. Теоретические основы электротехники: Теория электрических цепей и электромагнитного поля. Учеб. пособие для студ. высш. учеб. заведений/ С.А.Башарин,

В.В.Фёдоров. – М.: Издательский центр «Академия», 2004. – 304 с. ISBN 5-7695-1261-X.

11.Татур Т.А., Татур В.Е. Установившиеся и переходные процессы в электрических це-

пях: Учебное пособие для вузов. – М.: Высшая школа, 2001. – 408 с. ISBN 978-5-06- 003977-1.

12. Андреев В.С. Теория нелинейных электрических цепей. – М.: Радио и связь, 1982. – 280 с.

13. Данилов Л.В. Теория нелинейных электрических цепей/ Л.В.Данилов, П.Н.Матханов, Е.С.Филиппов. – Л.: Энергоатомиздат. Ленингр. отделение, 1990. – 256 с. ISBN 5-283- 04433-5.

14. Ануфриев И. E., Смирнов А. Б., Смирнова Е. Н. MATLAB 7 в подлиннике. – СПб.:

БХВ-Петербург, 2005. - 1104 с.: ил. ISBN 5-94157-494-0.

15.Чье Ен Ун, Шеин А.Б. Метод решения уравнений состояния электронных устройств. – Проектирование и технология электронных средств, 2012, № 1. – с. 19 – 25.

16.Чье Ен Ун, Шеин А.Б. Решение уравнений переменных состояния электронных уст-

ройств на основе обнуления невязки. – Проектирование и технология электронных

средств, 2014, № 1. – с. 17 – 20.

17.Малафеев С.И. Теория автоматического управления/ С.И. Малафеев, А.А. Малафеева.

– М.: Издательский центр «Академия», 2014. – 384 с. ISBN 978-5-4468-0230-2.

18.Курганов С.А., Филаретов В.В. Формирование уравнений состояния линейных электрических цепей с обобщёнными индуктивными сечениями и ёмкостными контурами. – Электричество, 2013, № 9.

19.Баринов В.А., Строев В.А. Моделирование и анализ стационарных и переходных режимов энергосистем и их объединений. – Электро, 2002, № 4. – с. 10-12.

20.Обухов С. Г., Коровин В. В. Математическое моделирование и визуализация процессов при исследовании устройств силовой электроники в учебной лаборатории. – Практическая силовая электроника, 2004, № 1.

Селезнёв В.Ю., Сбитнев С.А., Шмелёв В.Е., Горюшин Ю.А.

Новый матричный метод моделирования режимов магистральных и распределительных электрических сетей по трёхфазным схемам замещения

Abstract

Создание интеллектуальных электрических сетей требует совершенствования методов расчёта их разнообразных режимов. Для решения этой проблемы по заказу ОАО ФСК ЕЭС во Владимирском Государственном университете была выполнена научноисследовательская работа. При выполнении этой НИР создан матричный метод расчёта нормальных и нештатных режимов электроэнергетических сетей различных классов напряжений по полным трёхфазным схемам. В результате вычислительных экспериментов с разработанными моделями и алгоритмами показано, что погрешности расчётов режимов электрических сетей по полным трёхфазным схемам замещения на порядок меньше погрешностей расчётов режимов таких сетей по упрощённым однолинейным схемам замещения. Матричный метод расчёта нормальных и нештатных режимов электроэнергетических сетей по полным трёхфазным схемам является универсальным, так как он не имеет ограничений по классам напряжений анализируемых сетей и совокупности причин, вызывающих их несимметрию. Предлагаемый метод основан на матричных соотношениях теории электрических цепей, а также разработанных авторами технологии построения трёхфазных матричных моделей сетевых объектов и предложенном алгоритме сборки глобальной модели анализируемой сети. Особое внимание в работе уделено трансформаторным сетевым объектам, в т.ч. трёхфазным трансформаторам и автотрансформаторам. В частности, предложен оригинальный способ расчёта импедансных и адмиттансных матриц трёхфазных схем замещения трансформаторных объектов по их паспортным данным. Выработаны рекомендации по совершенствованию системы паспортных данных трансформаторных объектов, необходимых и достаточных для строгого определения параметров трёхфазных схем замещения. Точность моделирования названных и иных важнейших электросетевых объектов подтверждена сопоставлением результатов расчётного моделирования с данными телеизмерений в исследуемой сети. Новый метод расчёта режимов сетей является надёжной научной основой для построения интеллектуальных электрических сетей с возможной распределённой генерацией. Кроме этого, разработанный авторами новый метод расчета режимов сетей является универсальной научной основой для обеспечения надежной работы электрических сетей всех классов напряжений, обеспечения нормированного качества электрической энергии для разнообразных потребителей и их электромагнитной совместимости.

Введение

Новизна разработки заключается в декомпозиции сложных и сверхсложных ЭЭС на ряд характерных участков, состоящих из множества типовых сетевых объектов, которые в технологии программирования представляются самостоятельными типами данных со своими топологическими и электрофизическими матрицами; в создании расчётных методик вычисления элементов этих матриц по паспортным данным, а также в возможности детального расчёта штатных и нештатных режимов работы ЭЭС без составления схемы замещения всей анализируемой сети. Это важно, поскольку полная трёхфазная схема замещения даже относительно простого участка ЭЭС будет содержать как минимум сотни и даже тысячи элементов (а также узлов и ветвей), что чрезвычайно затруднит её зрительное восприятие. Тем не менее, предлагаемая технология сетевых объектов как типов данных позволяет легко получить информацию о режиме любой ветви схемы замещения в любом сетевом объекте анализируемого участка ЭЭС при невысоких требованиях к пользовательскому интерфейсу.

Теоретическая основа матричного метода расчёта установившихся режимов электроэнерге-

тических сетей различных классов напряжений по полным трёхфазным схемам замещения

В настоящее время наблюдается интенсивное развитие вычислительной техники и программного обеспечения (ПО). Существует достаточно мощное математическое ПО для инженерных и

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

Соседние файлы в папке Dista_MEFP

#
22.03.20151.93 Mб42Lekcii_MEFP.doc
#
22.03.2015477.63 Кб28Lekcii_MEFP.pdf
#
22.03.2015129.02 Кб19Rab_pr_mag_MEFP.doc
#
22.03.2015133.43 Кб16Rab_pr_mag_MEFP.pdf